CS224W—06 Theory of GNN

CS224W—06 Theory of GNN

How expressive are GNN?

回顾

GNN的框架：

GNN的训练工作流：

本章中我们将学习GNN的expressive power：即可以区分不同图结构的能力

局部邻居结构

本节中用节点颜色指代特征feature，同色即特征相同。如图中举例图中所有节点的特征都相同（黄色）。

图上的信息分为结构信息和特征信息，因为特征相同，所以无法仅凭特征来区分节点了（如果特征全都不一样，只需要看特征向量就能将节点区分开了）。让所有特征相同可以更好看出GNN如何捕捉结构信息。

如果我们只考虑图中每个节点周围的局部邻居结构

1. 节点1和节点5有不同的节点度数，因此他们的邻居结构不同。
2. 节点1和节点4虽然节点度数相同，但是他们的邻居的节点度数不同，因此邻居结构也不同。
3. 节点1和节点2则拥有相同的邻居结构。

所以，GNN的节点嵌入可以区分不同节点的局部邻居结构吗？在什么情况下会失败？接下来我们将理解GNN如何捕捉局部邻居结构，其中涉及到一个关键概念：计算图 Computational graph。

Computational graph

在每一层中，GNN聚合相邻节点的嵌入。 GNN通过由邻域定义的计算图生成节点嵌入。 例如：下图中节点1、2的计算图（2层GNN）

但是GNN只会看到节点特征，看不到123的节点ID，如下所示，两个计算图是一样的，而且节点特征都一样，因此GNN会对节点1和节点2产生相同的嵌入，无法进行区分。

一般来说，不同的节点邻居定义了不同的计算图：

计算图与每个节点周围的根子树结构相同。

• 根子树（rooted subtrees）：通过从根节点递归展开相邻节点来定义。

GNN将不同的根子树映射到不同的节点嵌入。

How expressive is a GNN？

函数 $f:X\to Y$ 是单射的（injective），如果它将不同的元素映射到不同的输出。

• 直觉：$f$ 保留了关于输入的所有信息。

表示能力最强的GNN应该单射地映射子树到节点嵌入。

一个观察：具有相同深度的子树可以通过从叶子结点迭代到跟节点的邻居信息来进行区别。

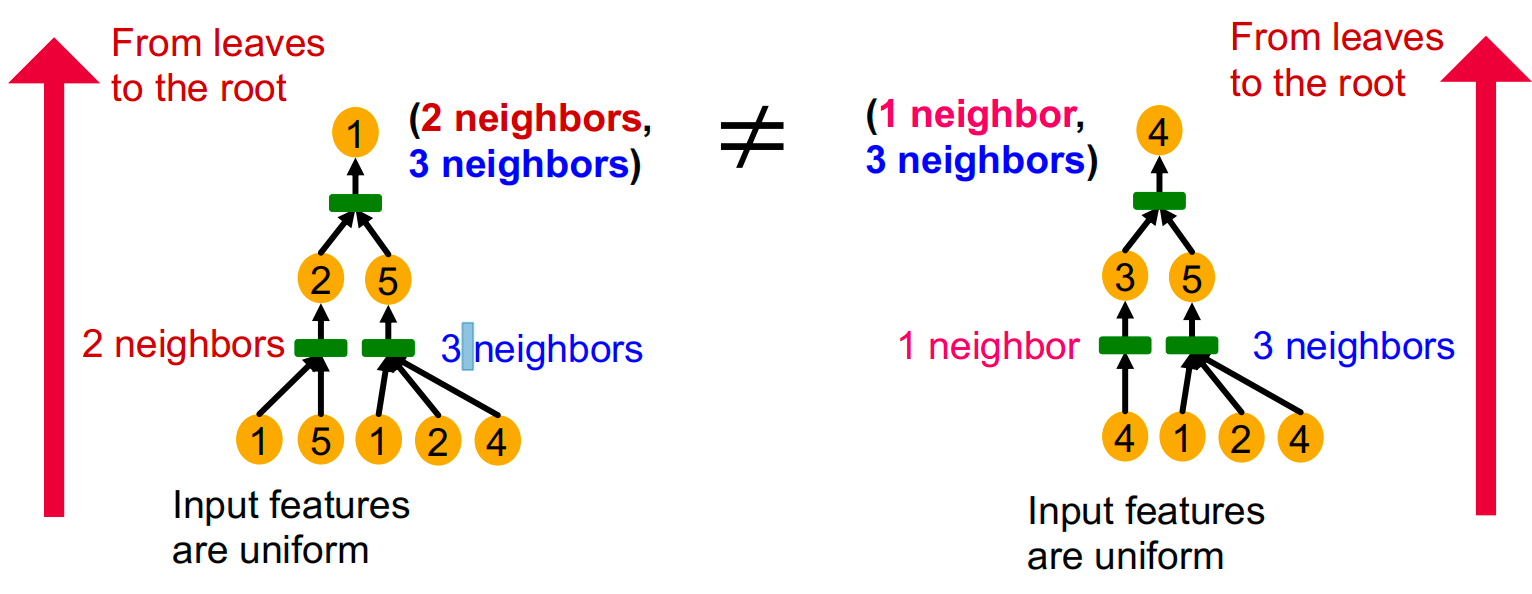
如果GNN每一步聚合都可以保留全部邻居信息，那么所产生的节点嵌入就可以区分不同的根子树。

换句话说，最具表现力的GNN会在每一步使用单射的邻居聚合函数。将不同的邻居映射到不同的嵌入。

做个总结：

• 为了生成节点嵌入，GNN使用与每个节点周围的根子树相对应的计算图。
• 如果GNN的每一步邻居聚合都是单射的，GNN可以完全区分不同的子树结构。
• 

Designing the Most Powerful Graph Neural Network

GNN的表示能力取决于其应用的邻居聚合函数。聚合函数表达能力越强，GNN表达能力越强，单射聚合函数的GNN表达能力最强。接下来本章节将理论分析各聚合函数的表示能力。

Neighbor Aggregation

观察：邻居聚合可以抽象为一个多集（包含重复元素的集合）上的函数。

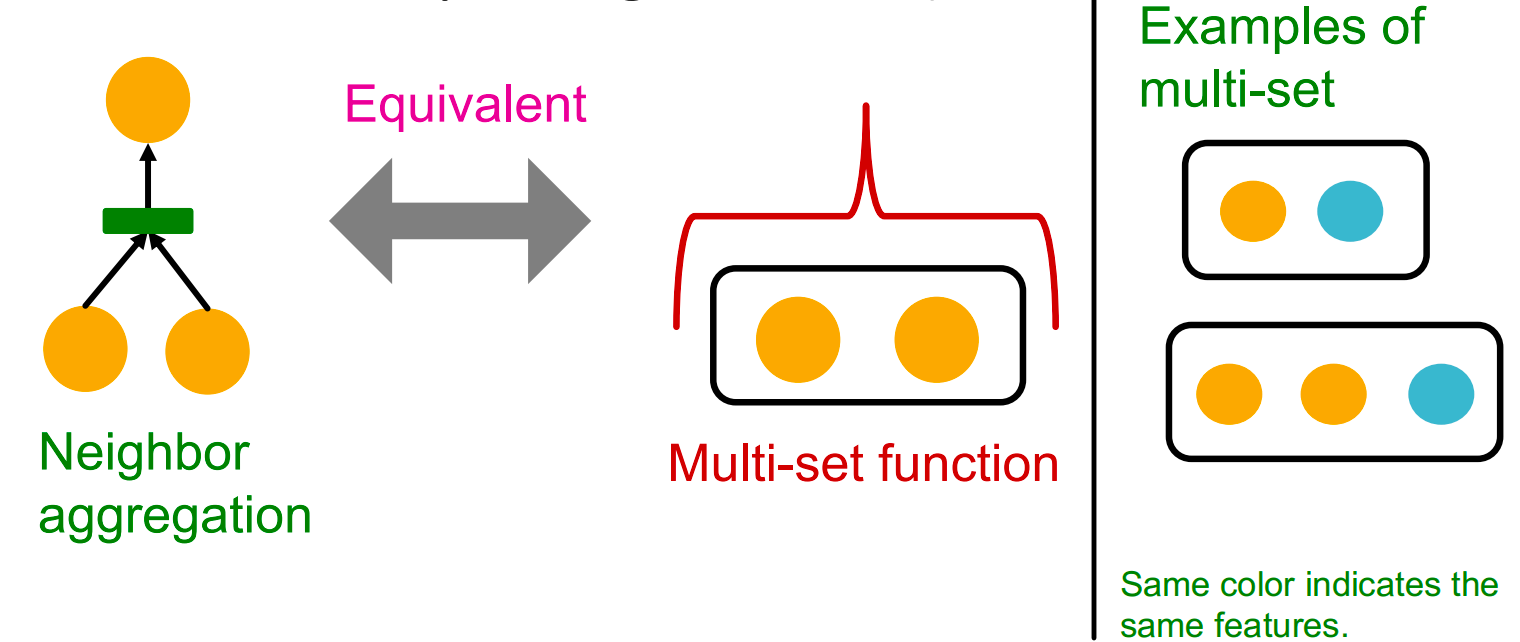
接下来分析两种流行GNN模型上的聚合函数

1. GCN：使用邻居节点特征的逐元素平均池化： Mean ( { x u } u ∈ N ( v ) ) \text{Mean}\left(\left\{x_u\right\}_{u \in N(v)}\right) Mean({xu​}u∈N(v)​)
2. GraphSAGE：使用邻居节点特征的逐元素最大池化 Max ⁡ ( { x u } u ∈ N ( v ) ) \operatorname{Max}\left(\left\{x_u\right\}_{u \in N(v)}\right) Max({xu​}u∈N(v)​)

GCN (mean-pool)：

• 线性函数、Relu激活、逐元素平均
• 根据Xu et al. ICLR 2019，得到定理：GCN的聚合函数无法区分颜色占比相同的multi-set。

GraphSAGE (max-pool)

• MLP、逐元素最大
• 根据Xu et al. ICLR 2019，GraphSAGE的聚合函数无法区分具有相同的不同颜色（即具有一样的多种颜色，或者不重复颜色组成的集合相同）。
• 

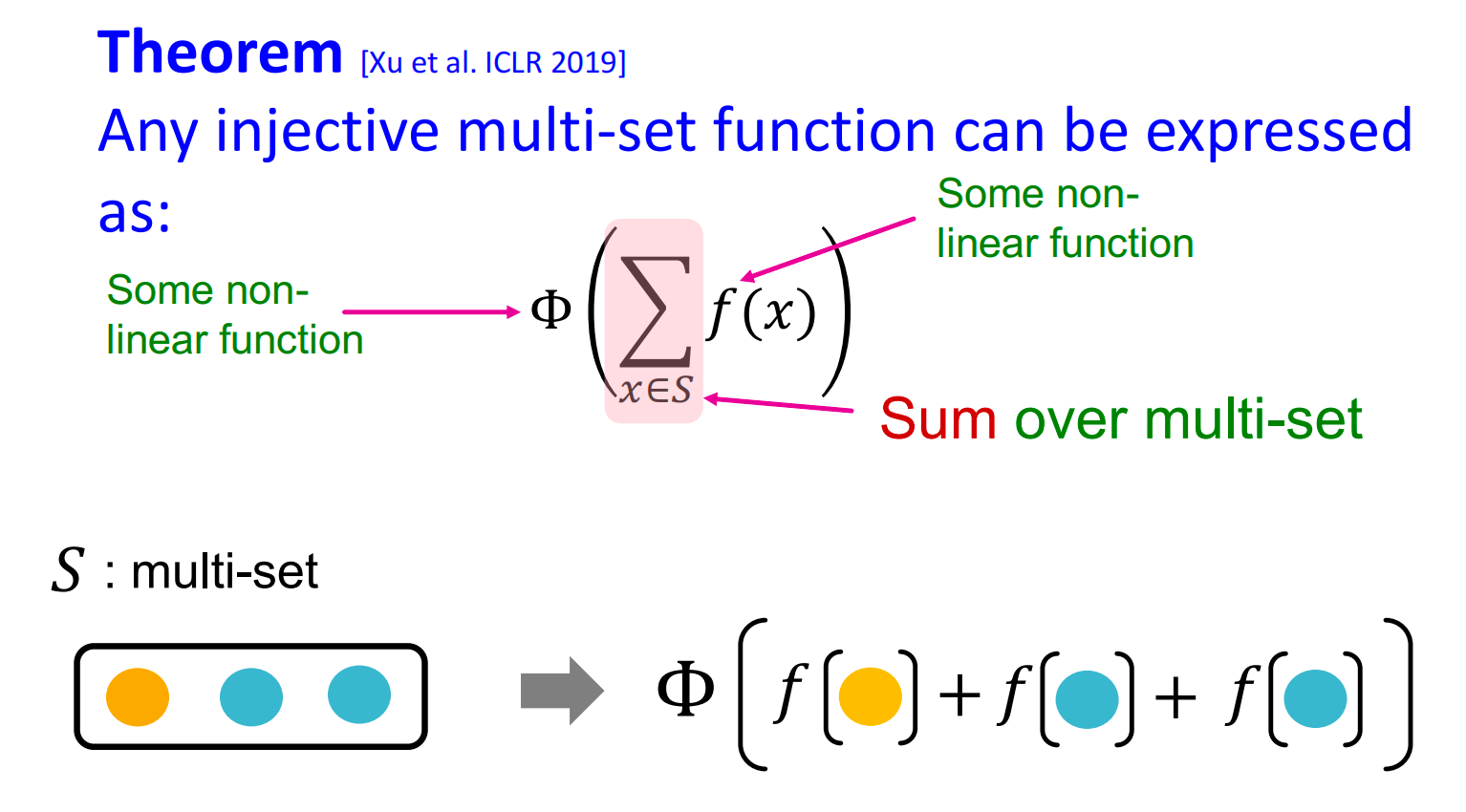
综合以上分析，GCN和GraphSAGE的表示能力并不是最强的。因此，我们需要设计一个可以建模单射多集合函数（injective multi-set function）的神经网络。

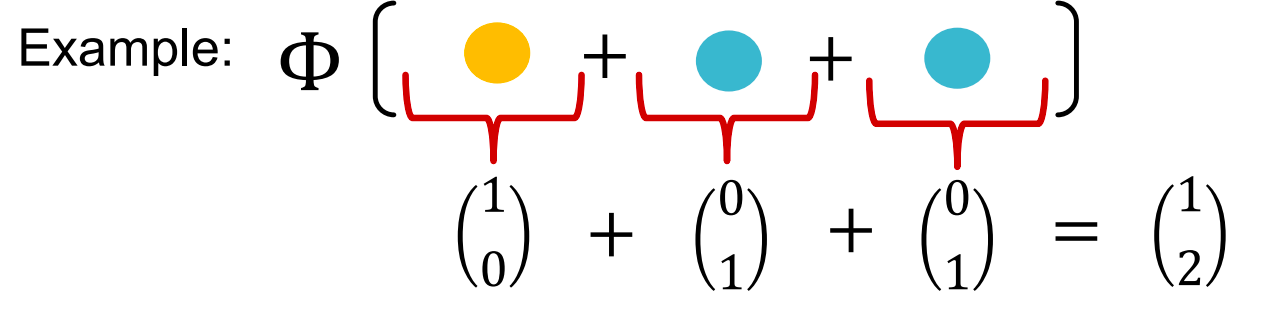
$f$ 产生颜色的一位有效编码。一位有效编码的总和保留了关于输入多集的所有信息。
$$\Phi \left(\sum _{x\in S}f(x)\right)$$

为了建模 $\Phi \left({\sum }_{x\in S}f(x)\right)$ 中的 $\Phi$ 和 $f$ ，我们使用MLP：

• 通用近似定理：只要一个隐藏层的MLP只要隐藏层维度够宽，并有合适的非线性函数 $\sigma (\cdot )$（包括ReLU和sigmoid），就可以任意精度逼近任何连续函数。
• ${\mathrm{MLP}}_{\Phi }\left({\sum }_{x\in S}{\mathrm{MLP}}_f(x)\right)$
• 在实践中，MLP的隐藏层维度在100-500就够了

Graph Isomorphism Network (GIN) 就使用了这种消息聚合方式，是单射的，也是我们目前学习到的最具有表示能力的消息传递类 GNN。

我们通过将GIN与WL graph kernel（获得图级别特征的传统方法）做关联，来全面了解GIN模型。
GIN可以说是WL graph kernel的神经网络版。

WL Graph Kernel

WL Graph Kernel 中的refinement 算法：

• 给定：一个图 $G$ 与一组节点 $V$。

• 为每个节点 $v$ 分配一个初始颜色 $c^{(0)}(v)$。

• 通过迭代细化节点颜色：

• c ( k + 1 ) ( v ) = HASH ⁡ ( c ( k ) ( v ) , { c ( k ) ( u ) } u ∈ N ( v ) ) , c^{(k+1)}(v) = \operatorname{HASH}\left(c^{(k)}(v), \{c^{(k)}(u)\}_{u \in N(v)}\right), c(k+1)(v)=HASH(c(k)(v),{c(k)(u)}u∈N(v)​),

• 其中 HASH 将不同的输入映射到不同的颜色。

• 在 $K$ 步颜色细化后，$c^{(K)}(v)$ 概括了 $K$ 跳邻域的结构。

示例如下：

如果两个图有相同的一组颜色，则他们是同构的。

GIN

GIN使用一个神经网络来建模单射HASH函数。具体来说，我们将在如下元组上建模单射函数：

可以建模如下：
$${\mathrm{MLP}}_{\Phi }\left((1+ϵ)\cdot {\mathrm{MLP}}_f(c^{(k)}(v)))+\sum _{u\in N(v)}{\mathrm{MLP}}_f(c^{(k)}(u))\right)$$
其中 $ϵ$ 是一个可学习的标量。

如果输入特征 $c^{(0)}(v)$ 表示为独热编码，直接相加即是单射的：

GIN的节点嵌入更新

• 给定：一个图 $G$ 与一组节点 $V$。

• 为每个节点 $v$ 分配一个初始向量 $c^{(0)}(v)$。

• 通过迭代更新节点向量：

• $$c^{(k+1)}(v)=\mathrm{GINConv}\left(\left\{c^{(k)}(v),{\left\{c^{(k)}(u)\right\}}_{u\in N(v)}\right\}\right),$$

• 其中 GINConv 将不同的输入映射到不同的嵌入。

• 在 $K$ 步 GIN 迭代后，$c^{(K)}(v)$ 概括了 $K$ 跳邻域的结构。

GIN可以被理解为WL Graph Kernel的可微分神经版本：

	更新目标	更新函数
WL图核	节点颜色（独热编码）	HASH
GIN	节点嵌入（低维向量）	GINConv

GIN相对于WL图核的优势包括：

• 节点嵌入是低维的；因此，它们能够捕捉不同节点的细粒度相似性。
• 更新函数的参数可以为下游任务学习。

由于GIN与WL graph kernel之间的关系，二者的表示能力是相同的，也就是对于一样的图，要么二者都能区分，要么都不能区分。在理论上和实践上，WL graph kernel都能区分现实世界的大部分图，因此GIN也能区分现实世界的大部分图。

参考资料

• https://web.stanford.edu/class/cs224w/
• http://t.csdnimg.cn/GfUFo