利用数据包络分析DEA模型利用DEAP工具对研发及各种工作工程进行评价

最新推荐文章于 2024-09-11 08:23:48 发布

林戈的IT生涯

最新推荐文章于 2024-09-11 08:23:48 发布

阅读量3.6k

点赞数 88

分类专栏：林戈个人专栏文章标签：数据包络分析 DEA模型 DEAP工具工程评价清华大学MEM

本文链接：https://blog.csdn.net/weixin_47792780/article/details/137868329

版权

林戈个人专栏专栏收录该内容

33 篇文章

订阅专栏

注：本文为清华大学一次课后作业所整理而成。publish:June 6, 2019 -Thursday

数据包络分析(data envelopment analysis)简称DEA,采用线性规划技术，是最常用的一种非参数前沿效率分析方法，以相对效率为基础对同一类型的部门的绩效进行评价。之前也没有接触过，上次上MEM课，清华大学刘大成教授布置了个作业，要利用数据包络分析方法和DEAP软件比较各自单位的绩效和改进方向，如果单位的DMU过少，也可以时间刻度进行纵向比较。也正因为这个作业，开始了解数据包络分析并查找相关的内容，使用之后感觉受益颇深，工作中涉及的很多评价我觉得都可以利用这个模型。

DEA将同一类型的部门或单位当作决策单元(DMU)，其评价依据的是所能观测到的决策单元的输入数据和输出数据。

输入数据：指决策单元在某种活动中所消耗的某些量，如投入资金量、原料量等，
输出数据：指决策单元消耗这些量所获得的成果和产出，如产品产量、收入金额等。

将各决策单元的输入输出数据组成生产可能集所形成的生产有效前沿面，通过衡量每个决策单元离此前沿面的远近，来判断该决策单元的投入产出的合理性，即技术效率。

有效前沿亦称“有效边界”。理性的投资者一般是厌恶风险而偏好收益的，对于相同的风险水平，会选择能提供最大收益率的组合；对于相同的预期收益率，会选择风险最小的组合。能同时满足这些条件的投资组合就是有效前沿。假设有多个业务部门进行绩效对比，就相当于根据投入产出将这些部门在坐标上安排好它们各自的位置，整个坐标点所覆盖的区域可以看成是可行区域，而有效生产前沿就是满足最优化条件的曲线，即是可行区域的边界。如下图：

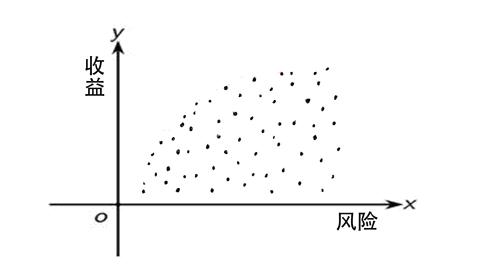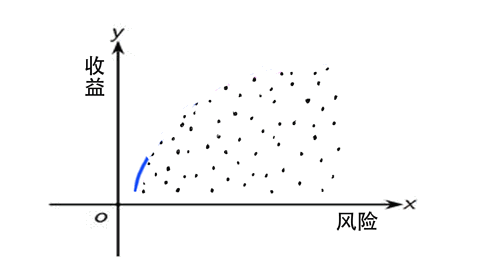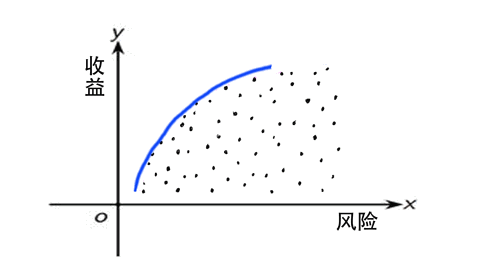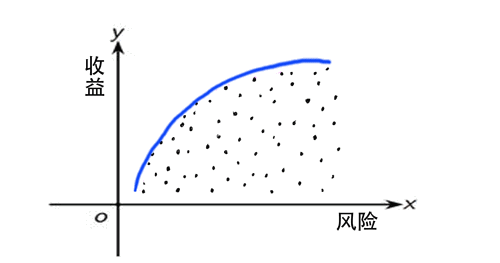
通常我们进行评价的方法比较同一类型的决策单元的效率时，需要先对决策单元的输入输出指标进行比较，并通过加权得到一个综合评分，然后通过各个决策单元的评分来反映其效益优劣。数据包络分析法则巧妙地构造了目标函数，并通过Charnes－Cooper变换（称为－变换）将分式规划问题转化为线性规划问题，无需统一指标的量纲，也无需给定或者计算投入产出的权值，而是通过最优化过程来确定权重，从而使对决策单元的评价更为客观。DEA是通过线性规划的方法来度量效率，它是一种非参数方法，即不需要已知生产前沿的具体形式，而只需已知投入产出的数据。DEA能方便容易处理决策单元是多产出情况。

Charnes，Cooper和Rhodes(1978)[6]提出了DEA中的第一个模型———CCR模型，该模型是其他DEA模型的基础。Banker，Charnes和Cooper(1984)提出了BCC模型，该模型将CCR模型中假定的规模报酬不变放宽为规模报酬可变。Andersen和Petersen(1993)提出了超效率模型。与上述模型相比，该模型重新计算了上述模型中效率为1的决策单元的效率，最终区分了原来都处于前沿面上决策单元的技术效率水平。在经济学中还有其他数十种DEA模型，但上述三种模型在我国应用最为普遍。

DEA方法也存在着一些缺点：首先，当决策单元总数与投入产出指标总数接近时，DEA方法所得的技术效率与实际情况偏差较大；其次，DEA方法对技术有效单元无法进行比较；此外，由于未考虑到系统中随机因素的影响，当样本中存在着特殊点时，DEA方法的技术效率结果将受到很大影响。彭晓英等用因子分析法对指标进行筛选和综合，再采用DEA方法进行评价，解决了DEA方法对指标数量限制的问题，并对煤炭资源型城市的生态经济发展进行了评价。

SFA与DEA方法都是前沿效率评价方法，它们都是通过构造生产前沿面来计算技术效率的。与DEA方法相比，SFA方法利用生产函数来构造生产前沿面，并采用技术无效率项的条件期望来作为技术效率，其结果受特殊点的影响较小且不会出现效率值相同且为1的情况，可靠性、可比性更好。SFA方法也有一些缺点，如处理多产出的情况时不如DEA方法方便，需要将多产出合并成一个综合产出；而投入指标过多时，由于指标间的相关关系，也会对结果的可靠性产生影响。周春应等、侯强等分别采用了SFA方法对我国区域经济技术效率和辽宁省城市技术效率进行了评价。

分析示例：如公司最近有开发任务，一个小组完成一个小型业务开发任务。因为研发业务很难进行产出量化，我这里选了一个向代码库svn提交的代码行数这个可量化并且有一定意义的数据来作为研发小组产出的量化指标。投入则是每个小组的人数，薪资成本以及开发的时间成本。以下是5个研发小组各自小组人数、研发时间、薪资成本以及提交到SVN的代码行数数据：

[指令设置]编辑指令文件：Bf1-ins.txt ：

BF1-dta.txt            DATA FILE NAME
BF1-out.txt            OUTPUT FILE NAME
5                NUMBER OF FIRMS
1		NUMBER OF TIME PERIODS 
1                NUMBER OF OUTPUTS
3                NUMBER OF INPUTS
0                0=INPUT AND 1=OUTPUT ORIENTATED
0		0=CRS AND 1=VRS
0		0=DEA(MULTI-STAGE), 1=COST-DEA, 2=MALMQUIST-DEA, 3=DEA(1-STAGE), 4=DEA(2-STAGE)

上面的各项解释如下：

[编辑数据文件]将上面的数据部分复制到待分析的数据文件：BF1-dta.txt。如下：

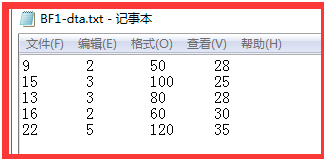
[DEAP计算]：运行DEAP.EXE输入文件名：Bf1-ins.txt，生成结果如下：

Results from DEAP Version 2.1
Instruction file = Bf1-ins.txt 
Data file          = BF1-dta.txt 
 Input orientated DEA
 Scale assumption: CRS
 Slacks calculated using multi-stage method
 
 #此项可以看到小于1的小组即为不达标的小组
 EFFICIENCY SUMMARY:
  firm     te
    1  0.675
    2  1.000
    3  0.795
    4  1.000
    5  1.000
 mean  0.894
 
 SUMMARY OF OUTPUT SLACKS:
 firm  output:           1
    1                0.000
    2                0.000
    3                0.000
    4                0.000
    5                0.000
 mean                0.000
 
 #此项能看到投入冗余，及哪些投入过多
 SUMMARY OF INPUT SLACKS:
 firm  input:            1           2           3
    1                0.225       0.000       2.025
    2                0.000      25.000       0.000
    3                0.000       2.187       0.000
    4                0.000       0.000       0.000
    5                0.000       0.000       0.000

 mean                0.045       5.437       0.405
 
 SUMMARY OF PEERS:
  firm  peers:
    1      4
    2      5    4
    3      5    4
    4      4
    5      5
 
 SUMMARY OF PEER WEIGHTS:
   (in same order as above)
  firm  peer weights:
    1   0.563
    2   0.500 0.250
    3   0.338 0.348
    4   1.000
    5   1.000
 
 PEER COUNT SUMMARY:
   (i.e., no. times each firm is a peer for another)
  firm  peer count:
    1       0
    2       0
    3       0
    4       3
    5       2
 
 SUMMARY OF OUTPUT TARGETS:
 firm  output:           1
    1                9.000
    2               15.000
    3               13.000
    4               16.000
    5               22.000
 
 
 SUMMARY OF INPUT TARGETS:
 firm  input:            1           2           3
    1                1.125      33.750      16.875
    2                3.000      75.000      25.000
    3                2.385      61.422      22.263
    4                2.000      60.000      30.000
    5                5.000     120.000      35.000
 
 
 #每个小组的详细分析数据。
 FIRM BY FIRM RESULTS:

Results for firm:     1
Technical efficiency = 0.675
 PROJECTION SUMMARY:
  variable           original        radial         slack     projected
                        value      movement      movement         value
 output     1           9.000         0.000         0.000         9.000
 input      1           2.000        -0.650        -0.225         1.125
 input      2          50.000       -16.250         0.000        33.750
 input      3          28.000        -9.100        -2.025        16.875
 LISTING OF PEERS:
  peer   lambda weight
    4      0.563
 
Results for firm:     2
Technical efficiency = 1.000
 PROJECTION SUMMARY:
  variable           original        radial         slack     projected
                        value      movement      movement         value
 output     1          15.000         0.000         0.000        15.000
 input      1           3.000         0.000         0.000         3.000
 input      2         100.000         0.000       -25.000        75.000
 input      3          25.000         0.000         0.000        25.000
 LISTING OF PEERS:
  peer   lambda weight
    5      0.500
    4      0.250
 
Results for firm:     3
Technical efficiency = 0.795
 PROJECTION SUMMARY:
  variable           original        radial         slack     projected
                        value      movement      movement         value
 output     1          13.000         0.000         0.000        13.000
 input      1           3.000        -0.615         0.000         2.385
 input      2          80.000       -16.391        -2.187        61.422
 input      3          28.000        -5.737         0.000        22.263
 LISTING OF PEERS:
  peer   lambda weight
    5      0.338
    4      0.348
 
Results for firm:     4
Technical efficiency = 1.000
 PROJECTION SUMMARY:
  variable           original        radial         slack     projected
                        value      movement      movement         value
 output     1          16.000         0.000         0.000        16.000
 input      1           2.000         0.000         0.000         2.000
 input      2          60.000         0.000         0.000        60.000
 input      3          30.000         0.000         0.000        30.000
 LISTING OF PEERS:
  peer   lambda weight
    4      1.000
 
Results for firm:     5
Technical efficiency = 1.000
 PROJECTION SUMMARY:
  variable           original        radial         slack     projected
                        value      movement      movement         value
 output     1          22.000         0.000         0.000        22.000
 input      1           5.000         0.000         0.000         5.000
 input      2         120.000         0.000         0.000       120.000
 input      3          35.000         0.000         0.000        35.000
 LISTING OF PEERS:
  peer   lambda weight
    5      1.000