组合数学&容斥&概率与期望

于 2022-08-12 10:59:32 发布
阅读量941 收藏 5
点赞数
分类专栏： Acm算法仓库，自用 文章标签： 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_48024524/article/details/126299928
版权

一、排列

1、不可重复排列

A n r   =   n ( n − 1 ) ( n − 2 ) . . . ( n − r + 1 ) {A}^{r}_{n}\, =\, n(n-1)(n-2)...(n-r+1) Anr​=n(n−1)(n−2)...(n−r+1)

A n r   =   n ! ( n   −   r ) ! {A}^{r}_{n}\, =\, \frac {n!} {(n\, -\, r)!} Anr​=(n−r)!n!​

2、可重复排列

n r {n}^{r} nr

3、圆排列

**定义：**有一组元素，将其排成一个圆，这种排列叫做圆排列或项链排列。

  • ​ n个数的圆排列为（n-1）！
  • ​ n个不同数中取r个的圆排列：

P n r r   =   A n r r   =   n ! ( n − r ) !   × r \frac {{P}^{r}_{n}} {r}\, =\, \frac {{A}^{r}_{n}} {r}\, =\, \frac {n!} {(n-r)!\, \times r} rPnr​​=rAnr​​=(n−r)!×rn!​

4、不尽相异元素全排列

定义：如果n个元素里，有p个元素相同，又有q个元素相同，…，又有r个元素相同（p+q+…+r≤n），则它们的所有排列种数为：
n ! p ! q ! . . . r ! \frac {n!} {p!q!...r!} p!q!...r!n!​

二、组合

1、不可重组合数

C n r   =   n ! r ! ( n − r ) ! {C}^{r}_{n}\, =\, \frac {n!} {r!(n-r)!} Cnr​=r!(n−r)!n!​

2、可重组合数（隔板法）

转换思路，既然要抽r次，就要放回r-1次，最后一次的放回对抽样结果无影响。

那么就变成我把r-1个物品放入n里，然后一次抽取k个。
H n r   =   C n + r − 1 r   =   ( n + r − 1 ) ! r ! ( n − 1 ) ! {H}^{r}_{n}{\, =\, C}^{r}_{n+r-1}\, =\, \frac {(n+r-1)!} {r!(n-1)!} Hnr​=Cn+r−1r​=r!(n−1)!(n+r−1)!​

3、不相邻组合数

3.1从n个球中选出r个球，要求r个球互不相邻

分析：

  • 当n<2r-1时，取法为0种
  • 当n≥2r-1时，取法为

   C n − r + 1 r   {\, \, C}^{r}_{n-r+1}\, Cn−r+1r​

理解思路：先从n中拿取r-1个球，然后我们在剩下的n-r+1个球中任取r个球，一开始的r-1个球填入r个球的空位中，这样就可以使r个球互不相邻。

3.2从n个围成一圈的球中选出r个球

分析：

当n<2r时，取法为0种

当n≥2r时，取法为
n C n − r r n − r \frac {{nC}^{r}_{n-r}} {n-r} n−rnCn−rr​​
理解思路： 无论怎么取，都是两种情况， 一种包括一号，另一种不包括一号。

包括一号：
C n − r − 1 r − 1 {C}^{r-1}_{n-r-1} Cn−r−1r−1​
不包括一号：
C n − r r {C}^{r}_{n-r} Cn−rr​

4、常用组合函数公式

C n r   =   C n − 1 r   +   C n − 1 r − 1 {C}^{r}_{n}\, =\, {C}^{r}_{n-1}\, +\, {C}^{r-1}_{n-1} Cnr​=Cn−1r​+Cn−1r−1​

C n r   =   C n n − r   {C}^{r}_{n}\ =\ {C}^{n-r}_{n}\ Cnr​ = Cnn−r​ 

C n r + 1   =   n − r r + 1 C n r   {C}^{r+1}_{n}\ =\ \frac {n-r} {r+1}{C}^{r}_{n}\ Cnr+1​ = r+1n−r​Cnr​ 

5、Lucas定理

适合用于n跟r都比较大，mod比较小（1e5 - 1e9）的情况。
C n r    %   m o d   =   C n / m o d r / m o d   ∗   C n % m o d r % m o d   %   m o d {C}^{r}_{n}\, \, \% \, mod\, =\, {C}^{r/mod}_{n/mod}\, *\, {C}^{r\% mod}_{n\% mod}\, \% \, mod Cnr​%mod=Cn/modr/mod​∗Cn%modr%mod​%mod

6、 错排问题

排列中n个元素都不在原来的位置上。

​ Dn=(n−1)(Dn−1+Dn−2) n>3,D1=0, D2=1

7、多重集公式

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jkZULopd-1660273010486)(D:\md\pic\image-20220727094729927.png)]

（3）跟（2）一样，但是取的r大于各k。
C k + r − 1 k − 1 −   ∑ i   =   1 k C k + r − n i − 2 k − 1 + ∑ 1 ≤ i < j ≤ k C k   + r   −   n i − n j − 3   k − 1 − . . . + ( − 1 ) k C k + r − ∑ i   = 1 k n i − ( k + 1 ) k − 1 {C}^{k-1}_{k+r-1}-\, \sum ^{k}_{i\, =\, 1} {{C}^{k-1}_{k+r-{n}_{i}-2}}+\sum _{1\leq i<j\leq k} {{C}^{k-1}_{k\, +r\, -\, {n}_{i}-{n}_{j}-3\, }}-...+{(-1)}^{k}{C}^{k-1}_{k+r-\sum ^{k}_{i\, =1} {{n}_{i}}-(k+1)} Ck+r−1k−1​−i=1∑k​Ck+r−ni​−2k−1​+1≤i<j≤k∑​Ck+r−ni​−nj​−3k−1​−...+(−1)kCk+r−∑i=1k​ni​−(k+1)k−1​
​

三、容斥定理

容斥原理是一种重要的组合数学方法，可以让你求解任意大小的集合，或者计算复合事件的概率。

1、描述

要计算几个集合并集的大小，我们要先将所有单个集合的大小计算出来，然后减去所有两个集合相交的部分，再加回所有三个集合相交的部分，再减去所有四个集合相交的部分，依此类推，一直计算到所有集合相交的部分。

2、用维恩图来表示

在这里插入图片描述

那么img的面积就是集合A、B、C各自面积之和减去img , img, img 的面积，再加上img的面积。

img

由此，我们也可以解决n个集合求并的问题。

3、用简单的例子来理解

3.1一个简单的排列问题

由0到9的数字组成排列，要求第一个数大于1，最后一个数小于8，一共有多少种排列？

​ 我们可以来计算它的逆问题，即第一个元素<=1或者最后一个元素>=8的情况。

​ 我们设第一个元素<=1时有X组排列，最后一个元素>=8时有Y组排列。那么通过容斥原理来解决就可以写成：

​ img

​ 经过简单的组合运算，我们得到了结果：

​ img

​ 然后被总的排列数10!减，就是最终的答案了。

3.2（0,1,2）序列问题

长度为n的由数字0，1，2组成的序列，要求每个数字至少出现1次，这样的序列有多少种？

​ 同样的，我们转向它的逆问题。也就是不出现这些数字的序列 不出现其中某些数字的序列。

​ 我们定义Ai(i=0…2)表示不出现数字i的序列数，那么由容斥原理，我们得到该逆问题的结果为：

img

​ 可以发现每个Ai的值都为2^n（因为这些序列中只能包含两种数字）。而所有的两两组合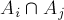img都为1（它们只包含1种数字）。最后，三个集合的交集为0。（因为它不包含数字，所以不存在）

​ 要记得我们解决的是它的逆问题，所以要用总数减掉，得到最终结果：

​ img

3.3 HDU 4153求指定区间内于n互素的数的个数

题目大意：

给出整数n和r。求区间[1;r]中与n互素的数的个数。

思路：

题目数据量很大，不能暴力枚举。
解决他的逆问题，求不与n互素的个数。
考虑n的所有素因子pi（i=1...k)
在[1;r]中有多少数能被pi整除呢？它就是：r/pi。
但是我们不能单纯的让所有结果相加，因为有很多数可以被统计很多次，所以这时候用到容斥定理来处理。

int solve (int n, int r)
{
    vector<int> p;
    for (int i=2; i*i<=n; ++i)
        if (n % i == 0)
        {
            p.push_back (i);
            while (n % i == 0)
                n /= i;
        }
    if (n > 1)
        p.push_back (n);

    int sum = 0;
    for (int msk=1; msk<(1<<p.size()); ++msk)//二进制枚举
    {
        int mult = 1,
            bits = 0;
        for (int i=0; i<(int)p.size(); ++i)
            if (msk & (1<<i))
            {
                ++bits;
                mult *= p[i];
            }

        int cur = r / mult;
        if (bits % 2 == 1)
            sum += cur;
        else
            sum -= cur;
    }

    return r - sum;
}

四、概率dp， 期望dp

4.1概率

概率加法

  1. 互不相交的事件，P(A或B发生)=P(A)+P(B)
  2. 如果A和B所涵盖的结果有交集，那么P(A或B发生)=P(A)+P(B)-P(A与B同时发生)

概率乘法

  1. 在两个 互不干扰的事中，事件A在其中一件事中，事件B在另外一件事中

    那么P(A与B同时发生)=P(A)P(B)

  2. 掷两个骰子，P(第一个点数小于3且第二个点数为偶数)=(2/6)(3/6)=1/6

4.2期望

  1. 事件A有多种结果，记其结果的大小为x，那么x的期望值表示 事件A 的结果的平均大小，记作E(x)。

  2. E(x)=每种结果的大小与其概率的乘积的和。

    例如，记掷一枚骰子的点数为x

    E(x)=1*(1/6)+2*(1/6)+3*(1/6)+4*(1/6)+5*(1/6)+6*(1/6)=7/2

  3. 若c为常数，那么：
    E(x+c)=E(x)+c，E(c*x)=c * E(x)

  4. 期望加法-----期望线性 性
    记两个事件的结果分别为x,y
    E(x+y)=E(x)+E(y)
    例如：E(语文成绩+数学成绩)=E(语文成绩)+E(数学成绩)

4.3概率与期望dp

概述

由于概率和期望具有线性性质，使得可以在概率和期望之间建立一定的递推关系，这样就可以通过动态规划来解决一些概率问题，例如概率和期望的最值问题就常常使用概率 DP、期望 DP 来解决。

概率dp

概率 DP 通常已知初始的状态，然后求解最终达到目标的概率，因此概率 DP 需要顺序求解。

其相较于期望 DP较为简单，当前状态只需加上所有上一状态乘上转移概率即可，即：f[i]=f[i-1]*p[i]

期望 dp

期望 DP 与概率 DP 不同，其需要倒序求解。

当求解达到某一目标的期望花费时，由于最终的花费无从知晓（无法从无穷推起），因此期望 DP 需要倒序求解。

设 f[i] 为 i 状态下实现目标的期望值，即到了 f[i] 这个状态的差距是多少。

初始时，令 f[n]=0，即在目标状态期望值为 0，然后进行状态转移，新的状态为上一状态与转移概率的乘积再加上转移的花费

即：*f[i-1]=f[i]p[i]+w

最后初始位置 f[0] 即为所求的期望值。

例题

题意：给定一个n面的骰子，问投出n个不同的面的期望投掷次数。 （1<=n<=1000）

分析：先考虑逆向转移,dp[n]=0 表示投出n个不同面之后，要达到投出n个不同面的状态还需要投掷0次。

即：dp[i]表示已经投出了i个面，要投出剩余n-i面的期望次数。

对于当前状态为i，投一次骰子，有i/n的可能投中已经出现的i个面之一，此情况下还需要投dp[i]次
					   有(n-i)/n的可能投出其余n-i面。此情况下还要投dp[i+1]次
即：由于投出的面可能出现过，也可能没出现过，所以dp[i]由dp[i] 与 dp[i+1] 转移而来
dp[i]=dp[i]*(i/n) + dp[i+1]*((n-i)/n) +1   （+1是因为要投一次骰子才能转移）
移项变成：dp[i]=dp[i+1] + n/(n-i)

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pii pair<int,int>
const int maxn = 2e3+5;
const int mx = 40;
const int mod = 1e9+5;
const ll inf = 34359738370;
const int INF = 1e9+7;
//给定n面的骰子 求投的期望次数 满足每面都至少出现一次
double dp[maxn];//dp[i] 表示已经出现i个面时  投出剩余n-i面的期望次数 dp[n]=0
//再投一次 i/n的几率投中已经有的面，此情况下还需要投dp[i]次骰子，(n-i)/n几率投中新的面  此情况下还要投dp[i+1]次
//dp[i]=(i/n)dp[i] + (n-i)/n *dp[i+1] +1
//(n-i)/n * dp[i]= (n-i)/n *dp[i+1] +1
//dp[i]=dp[i+1] + n/(n-i)
int main()
{
    int t;scanf("%d",&t);
    while(t--)
    {
        int n;
        scanf("%d",&n);
        dp[n]=0.0;
        for(int i=n-1;i>=0;--i)
        {
            dp[i]=dp[i+1] + 1.0*n/(n-i) ;
        }
        printf("%.2f\n",dp[0]);
    }
    return 0;
}

板子

一、排列组合数

1、费马小定理（要求模数为质数）

复杂度O(nlogn)，当n到1e7时就炸，这时候要用线性递推。

typedef long long ll;
const ll maxn = 1e6+10, mod = 1e9+7;
ll Jc[maxn];
void calJc()    //求maxn以内的数的阶乘
{
    Jc[0] = Jc[1] = 1;
    for(ll i = 2; i < maxn; i++)
        Jc[i] = Jc[i - 1] * i % mod;
}
ll pow(ll a, ll n, ll mod)    //快速幂 a^n % p
{
    ll ans = 1;
    while(n)
    {
        if(n & 1) ans = ans * a % mod;
        a = a * a % mod;
        n >>= 1;
    }
    return ans;
}
ll niYuan(ll a)   //费马小定理求逆元
{
    return pow(a, mod - 2, mod);
}
ll C(ll n, ll r)    //计算C(n, r)
{
    if(r>n)return 0;
    return Jc[n] * niYuan(Jc[r]) % mod
        * niYuan(Jc[n - r]) % mod;
}
ll A(ll n, ll r)
{
    return Jc[n] * niYuan(Jc[n-r])%mod;
}

2、拓展欧几里得（不要求模数为质数）

复杂度同上，关键点在他的模数不需要是质数。

typedef long long ll;
const ll maxn = 1e6+10, mod = 1e9+7;
ll Jc[maxn];
void calJc()    //求maxn以内的数的阶乘
{
    Jc[0] = Jc[1] = 1;
    for(ll i = 2; i < maxn; i++)
        Jc[i] = Jc[i - 1] * i % mod;
}
void exgcd(ll a, ll b, ll &x, ll &y)    //拓展欧几里得算法
{
    if(!b) x = 1, y = 0;
    else
    {
        exgcd(b, a % b, y, x);
        y -= x * (a / b);
    }
}
ll niYuan(ll a)   //求a对b取模的逆元
{
    ll x, y;
    exgcd(a, mod, x, y);
    return (x + mod) % mod;
}
ll C(ll n, ll r)    //计算C(n, r)
{
    if(r>n)return 0;
    return Jc[n] * niYuan(Jc[r]) % mod
        * niYuan(Jc[n - r]) % mod;
}
ll A(ll n, ll r)
{
    return Jc[n] * niYuan(Jc[n-r])%mod;
}

3、逆元-线性递推(p是质数)

typedef long long ll;
const ll maxn = 1e7+10, mod = 1e9+7;
ll Jc[maxn];
ll inv[maxn+5];
void getInv(ll mod)
{
    inv[1]=1;
    for(int i=2;i<maxn;i++)
        inv[i]=(mod-mod/i)*inv[mod%i]%mod;
}
void calJc()    //求maxn以内的数的阶乘
{
    Jc[0] = Jc[1] = 1;
    for(ll i = 2; i < maxn; i++)
        Jc[i] = Jc[i - 1] * i % mod;
}


ll C(ll n, ll r)    //计算C(n, r)
{
    if(r>n)return 0;
    return Jc[n] * inv[Jc[r]] % mod
        * inv[Jc[n - r]] % mod;
}
ll A(ll n, ll r)
{
    return Jc[n] * inv[Jc[n-r]]%mod;
}

4、Lucas定理

typedef long long ll;
const ll maxn = 1e6+10, mod = 1e9+7;
ll Jc[maxn];
void calJc()    //求maxn以内的数的阶乘
{
    Jc[0] = Jc[1] = 1;
    for(ll i = 2; i < maxn; i++)
        Jc[i] = Jc[i - 1] * i % mod;
}
void exgcd(ll a, ll b, ll &x, ll &y)    //拓展欧几里得算法
{
    if(!b) x = 1, y = 0;
    else
    {
        exgcd(b, a % b, y, x);
        y -= x * (a / b);
    }
}
ll niYuan(ll a)   //求a对b取模的逆元
{
    ll x, y;
    exgcd(a, mod, x, y);
    return (x + mod) % mod;
}
ll C(ll n, ll r)    //计算C(n, r)
{
    if(r>n)return 0;
    return Jc[n] * niYuan(Jc[r]) % mod
        * niYuan(Jc[n - r]) % mod;
}
ll A(ll n, ll r)
{
    return Jc[n] * niYuan(Jc[n-r])%mod;
}
ll Lucas(ll n,ll r)
{
    if(n<mod && r<mod)return C(n,r);
    else return C(n%mod, r%mod)*Lucas(n/mod, r/mod)%mod;
}

题单

大部分题解都在网址：(13条消息) CSWish的博客_CSDN博客-计算几何,组合数学,概率与期望领域博主

题目难度思路
HDU-1796 How many integers can you find⭐⭐基础容斥
HDU 4135 Co-prime⭐⭐基础容斥
HDU 3944 DP？⭐⭐Lucas求组合排列
UVA 11806 Cheerleaders⭐⭐基础容斥
Topcoder 10875⭐⭐错排，这道题主要是感受一下错排的用法，topcoder的做法跟常规不太一样，不需要细扣
HDU 2204 Eddy’s爱好⭐⭐⭐容斥原理
HDU 4407 Sum⭐⭐⭐容斥原理
HDU 2841 Visible Trees⭐⭐容斥原理
POJ 2773 Happy 2006⭐⭐⭐二分+容斥
AcWing 213古代猪文⭐⭐Lucas定理+中国剩余定理
AcWing 214 Devu and Flowers⭐⭐⭐多重集合的组合数
AcWing 216 Rainbow 的信号⭐⭐⭐位运算，概率与期望
HDU 5159⭐⭐简单求期望
Uva 11021⭐⭐概率dp入门
AcWing 233换教室⭐⭐⭐⭐不能实时决策，要考虑的状态比较多
AcWing 232 守卫者挑战⭐⭐⭐概率dp
AcWing 218 扑克牌⭐⭐⭐期望dp
AcWing 217 绿豆蛙的归宿⭐⭐期望dp
AcWing 216 rainbow的信号⭐⭐⭐位运算，期望dp
P 1297 单选错位(期望)⭐期望入门
p 1654⭐⭐⭐期望推导
poj 3071⭐⭐概率dp
codefroces 148d⭐⭐概率dp
poj 2151⭐⭐⭐概率dp
zoj 3380⭐⭐⭐概率dp
poj 2096⭐⭐逆推期望
hdu 4405⭐⭐结论题
zoj 3329⭐⭐⭐⭐期望

资料参考：

(24条消息) ACM-组合数学完全总结（知识点+模板）_Ogmx的博客-CSDN博客_组合数学

容斥原理（翻译） - vici - C++博客 (cppblog.com)

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值