【更新中】人教版高一数学知识点汇总（必修1）

必修一

一、集合

1.集合的概念

集合={元素1，元素2，…}

2.集合的性质

确定性（集合的元素是确定的）

{身高170的人} √
{身高较高的人} ×

互异性（一个集合中的元素是不重复出现的）

{0，1，2，3，4，4，5} ×

无序性（只要构成两个集合的元素相同，两个集合就是相等的）

{0，1，2，3，4，5}与{1，2，3，4，0，5}是相等的

3.数学中常用数集

（1）全体非负整数组成的集合称为非负整数集（或自然数集）：N
（2）所有正整数组成的集合称为正整数集 ：N*或N+
（3）全体整数组成的集合称为整数集： Z
（4）全体有理数组成的集合称为有理数集： Q
（5）全体实数组成的集合称为实数集： R

4.描述集合的方法

列举法

{0，1，2，3，4}
{西瓜，香蕉，苹果，菠萝}

描述法

D = { x ∈ R ∣ x < 10 } \mathbf{D}=\{x∈R|x<10\} D={ x∈R∣x<10}

图像法

韦恩图（Venn图）：

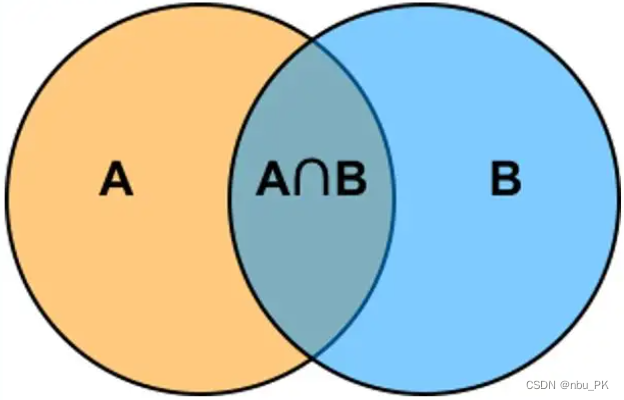
区间法

$$x\in [1,5]$$

5.集合间的基本关系

子集

对于两个集合A，B，如果集合A中任意一个元素都是集合B中的元素，则这两个集合有包含关系，称集合A为集合B的子集，记作：
$$A\subseteq B（或A\supseteq B）$$
读作“A含于B”（或“B包含A”）
如果$$\begin{gathered} A\subseteq B \\ B\subseteq A \end{gathered}$$那么集合A与集合B相等，记作：$$A=B$$
子集个数：2ⁿ（n为元素个数）

真子集

如果$$A\subseteq B$$但存在$$A\in B，且a\notin A$$我们称集合A是集合B的真子集，记作：
$$A⊊B（或B⊋A）$$
真子集个数：2ⁿ-1（n为元素个数）

空集

我们把不含任何元素的集合称为空集，记作：$$\varnothing$$空集是任何集合的子集。

6.集合的基本运算

并集

A ∪ B = { x ∣ x ∈ A , 或 x ∈ B } \mathbf{A∪B}=\{x|x∈A,或x∈B\} A∪B={ x∣x