从认识AI开始-----卷积神经网络（CNN）-CSDN博客

本文链接：https://blog.csdn.net/weixin_48222697/article/details/148264990

前言

在上一篇文章里，我们手写了多层感知机，细心地小伙伴们可能会发现一个问题，对于MLP，有两个突出的问题，尤其是处理图像任务时：

参数太多：例如一个28*28的图像扁平化为784维后，连接一个256个神经元的隐藏层就需要784*256=200704个权重参数。
空间结构丢失：MLP无法感知像素之间的空间布局，图像各像素之间的绝对位置信息与相对位置信息完全被打乱。

此时，急切需要一种更聪明的模型出现，那就是今天我要讲的卷积神经网络（CNN）。它通过局部连接和参数共享来有效减少参数的数量，同时，也保留了图像的空间结构信息，相比MLP而言，实现了更强大的学习能力。

一、卷积神经网络的两个动机：局部性与平移不变性

1. 局部性

我们知道，在图像中，一个像素点的类别往往由其附近的像素共同决定，比如一张小狗图像，其中眼睛部分是有多个像素点共同决定的。因此，我们无需全连接每一个像素与神经元，而是让神经元只感知图像中的一个局部区域，例如4*4 区域，这就是我们常说的“感受野”的概念。

感受野的存在让网络能够首先捕捉局部特征，然后再逐层组合形成全局特征。

2. 平移不变性（参数共享）

所谓的平移不变性其实很好理解，就是我们在图像中使用相同的卷积核在图像上滑动，相当于使用同一组权重探测图像的所有位置，这同时也是“卷积”的概念：

$input(image_{x,y})=\sum _{i,j}W_{i,j}*image_{x+i,y+j} + b_{i,j}$

通过上面的公式我们可以看出，相比于全连接，卷积操作大大降低了参数数量，一个卷积核可能只有3*3=9个参数，同时，卷积操作在移动的过程中是用的同一个卷积核，也带来了平移不变性：即使不同图片里的相同特征出现在不同的位置，特征仍可被捕捉，例如一只鸟出现在图像的左上角，那么使用同一个卷积核，即使该鸟出现在图片的右下角，该鸟所具有的特征仍能被捕捉到。

二、卷积神经网络的基本结构：

对于一个典型的CNN来说，需要包括以下几个结构：

1. 卷积层：

所谓的卷积层，就是：用一个卷积核（小窗口）在图像上进行滑动，与区域内像素做加权和。具体的公式可以写成这样：

设输入图像为 $X\in\mathbb{R}^{H*W}$ ，卷积核 $K\in\mathbb{R}^{k*k}$ ，输出 $y\in\mathbb{R}^{(H-k+1)*(W-k+1)}$ :

$y(i,j)=\sum_{u=0}^{k-1}\sum_{v=0}^{k-1}X(i+u,j+v)*K(u,v)$

其计算过程如下图所示：

接下来，我将手写一下具体的卷积操作的代码流程，对具体操作感兴趣的小伙伴们可以看一下：

import torch
import numpy as np

class conv2d(nn.Module):
    def __init__(self, kernel_size):
        super(conv2d, self).__init__()
        self.kernel_size = kernel_size
        self.w = nn.Parameter(torch.rand(kernel_size))
        self.b = nn.Parameter(torch.zeros(1))
    def conv(self, X, K):
        H, W = K.shape
        y = torch.zeros(X.shape[0]-H+1, X.shape[1]-W+1)
        for i in range(y.shape[0]):
            for j in range(y.shape[1]):
                y[i,j] = (X[i:i+H, j:j+W] * K).sum()
        return y
    def forward(self, x):
        return self.conv(x, self.w) + self.b

# 示例
mycnn = conv2d(kernel_size=(3,3))
x = torch.arange(25, dtype=torch.float32).reshape(5,5)

output = mycnn(x)
print(output, output.shape)

2. 填充（Padding）

无填充时，图像边缘信息会被逐层压缩掉，Padding的目的是保留边缘特征，同时，经过padding后，能控制输出的尺寸。填充减小的输出大小与层数具有线性相关性。

常见填充有两种：

padding = 0：无填充时，尺寸缩小
padding= 1：即上下左右同时填充行和一列，能够使输入输出尺寸一致
padding通常取核大小减1

让我们通过下面的图片来看具体的padding过程：

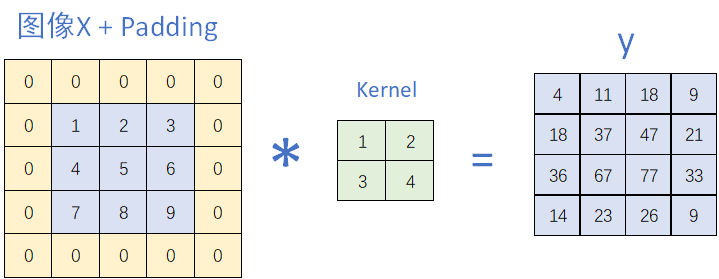
接下来，我将手写一下具体的pddding操作的代码流程，在conv中添加padding：

import torch
import torch.nn as nn
import torch.nn.functional as F

class conv2d(nn.Module):
    def __init__(self, kernel_size, padding=0):
        super(conv2d, self).__init__()
        self.kernel_size = kernel_size
        self.padding = padding
        self.w = nn.Parameter(torch.rand(kernel_size))
        self.b = nn.Parameter(torch.zeros(1))
    def conv(self, X, K):
        H, W = K.shape
        if self.padding > 0:
            X = F.pad(X, (self.padding, self.padding, self.padding, self.padding), mode='constant', value=0)
        y = torch.zeros(X.shape[0]-H+1, X.shape[1]-W+1)
        for i in range(y.shape[0]):
            for j in range(y.shape[1]):
                y[i,j] = (X[i:i+H, j:j+W] * K).sum()
        return y
    def forward(self, x):
        return self.conv(x, self.w) + self.b

3. 步幅（stride）

步幅的作用也很重要，具体来说：控制卷积核的滑动速度，从而影响下采样。

步幅越大，输出的尺寸越小，计算越快，但信息更稀疏。步幅减小的输出大小与层数的指数相关：

stride = 1：默认滑动一步，最大限度的保留特征
stride = 2：相当于下采样

接下来，我将手写一下具体的Stride操作的代码流程，在conv中添加Stride：

import torch
import torch.nn as nn
import torch.nn.functional as F

class conv2d(nn.Module):
    def __init__(self, kernel_size, padding=0, stride=1):
        super(conv2d, self).__init__()
        self.kernel_size = kernel_size
        self.padding = padding
        self.stride = stride
        self.w = nn.Parameter(torch.rand(kernel_size))
        self.b = nn.Parameter(torch.zeros(1))
    def conv(self, X, K):
        H, W = K.shape
        if self.padding > 0:
            X = F.pad(X, (self.padding, self.padding, self.padding, self.padding), mode='constant', value=0)
        y = torch.zeros((X.shape[0]-H)//self.stride + 1, (X.shape[1]-W)//self.stride + 1)
        for i in range(y.shape[0]):
            for j in range(y.shape[1]):
                xi = i * self.stride
                xj = j * self.stride
                y[i,j] = (X[i:xi+H, j:xj+W] * K).sum()
        return y
    def forward(self, x):
        return self.conv(x, self.w) + self.b

4. 池化层（Pooling）

之所以会设计池化层，主要是因为卷积层对于图像的位置信息很敏感：

降低维度
保留关键信息（如边缘、纹理）
增加一定程度的平移不变性，从而降低对位置的敏感性

接下来，我将手写一下具体的Pooling操作的代码流程，以最大池化为例：

import torch
import torch.nn as nn

class maxpool2d(nn.Module):
    def __init__(self, kernel_size, stride=None):
        super(maxpool2d, self,).__init__()
        self.kernel_size = kernel_size
        self.stride = stride or kernel_size
    def forward(self, x):
        H, W = x.shape
        KH, KW = self.kernel_size, self.kernel_size
        SH, SW = self.stride, self.stride
        y = torch.zeros((H-KW)//SH + 1,(W-KW)//SW + 1)
        for i in range(y.shape[0]):
            for j in range(y.shape[1]):
                xi = i * SH
                xj = j * SW
                y[i,j] = x[xi:xi+KH, xj:xj+KW].max()
        return y

5. 输出尺寸与输入尺寸、卷积核、填充、步幅的关系

输出尺寸与输入大小、卷积核大小、填充、步幅具有下述关系：

$O=\frac {N+2P-K}{S}+1$

其中， $N$ 为输入尺寸， $P$ 为padding， $K$ 为卷积核尺寸， $S$ 为步幅大小

三、多通道输入

在现实世界中，大多数图片都是RGB三通道，比如，对于大小为32*32的RGB图像，其形状就是[3， 32， 32]，有三个输入通道，这三个通道分别包含不同的颜色信息，缺少任何一个通道都会导致图像特征信息丢失。具体做法如下：

通常，在卷积层中，我们需要为每个输入通道分配一个卷积核，每个卷积核会在输入通道上滑动，从不同视角捕捉局部结构信息（比如边缘、纹理等），多个输入通道意味着模型可以并行提取多种不同类型的特征，提升表达能力。

具体表达形式如下：

$y^{out}=\sum_{c=1}^{C_{in}}X_c^{in} * W_c + b$

其中， $X_c^{in}$ 为第c个输入通道， $W_c$ 对应第 c 哥输入通道的卷积核， b 为偏置

接下来，我将手写具体的多通道输入代码，各位感兴趣的小伙伴们可以了解一下：

import torch
import torch.nn as nn
import torch.nn.functional as F

class Conv2D(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size, padding=0, stride=1):
        super(Conv2D, self).__init__()
        if isinstance(kernel_size, int):
            kernel_size = (kernel_size, kernel_size)
        self.kernel_size = kernel_size
        self.padding = padding
        self.stride = stride
        self.in_channels = in_channels
        self.out_channels = out_channels

        # 权重形状: [out_channels, in_channels, kH, kW]
        self.w = nn.Parameter(torch.rand(out_channels, in_channels, *kernel_size))
        self.b = nn.Parameter(torch.zeros(out_channels))

    def conv(self, X, K):
        # X: [in_channels, H, W]
        in_channels, H, W = X.shape
        kH, kW = K.shape[-2], K.shape[-1]

        # 进行 padding
        if self.padding > 0:
            X = F.pad(X, (self.padding, self.padding, self.padding, self.padding), mode='constant', value=0)

        H_out = (X.shape[1] - kH) // self.stride + 1
        W_out = (X.shape[2] - kW) // self.stride + 1

        Y = torch.zeros((self.out_channels, H_out, W_out))

        # 多输出通道
        for oc in range(self.out_channels):
            for i in range(H_out):
                for j in range(W_out):
                    region_sum = 0.0
                    for ic in range(self.in_channels):
                        h_start = i * self.stride
                        h_end = h_start + kH
                        w_start = j * self.stride
                        w_end = w_start + kW
                        region = X[ic, h_start:h_end, w_start:w_end]
                        region_sum += (region * K[oc, ic]).sum()
                    Y[oc, i, j] = region_sum + self.b[oc]
        return Y

    def forward(self, x):
        # x: [in_channels, H, W]
        return self.conv(x, self.w)
# 示例 3通道输入，32x32图像
x = torch.randn(3, 32, 32)  
conv = Conv2D(in_channels=3, out_channels=2, kernel_size=3, padding=1, stride=1)
y = conv(x)
# torch.Size([2, 32, 32])
print(y.shape)

四、使用Pytorch内置函数构建基础CNN模型

接下来，我将使用Pytorch内置的卷积层来构建一个基础的CNN网络，进行手写数字识别（MINST）：

import torch
import torch.nn as nn
import torch.nn.functional as F

class cnn(nn.Module):
    def __init__(self, ):
        super(cnn, self).__init__()
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=16, kernel_size=3, padding=1)
        self.pool = nn.MaxPool2d(kernel_size=3, stride=2)
        self.conv2 = nn.Conv2d(16,32,3,padding=1)
        self.fc1 = nn.Linear(32*7*7, 128)
        self.fc2 = nn.Linear(128, 10)
    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = self.pool(x)
        x = F.relu(self.conv2(x))
        x = self.pool(x)    
        x = x.view(x.size(0), -1)
        x = self.fc1(x)
        x = F.relu(x)
        x = self.fc2(x)
        return x
# 示例
model = cnn()
# [batch, channel, H, W]
x = torch.randn(4,1,28,28)
output = model(x)
print(output.shape)

总结

以上就是本文的全部内容，相信小伙伴们在看完本篇之后会对卷积神经网络有更深刻的理解：CNN作为深度学习中处理图像、语音、视频等具有空间数据的模型，其设计核心在于：局部连接模拟生物视觉感知，关注局部区域特征；参数共享能显著减少模型参数；平移不变性与池化操作能降低CNN对位置的敏感性。相较于传统的MLP，CNN的具有低参数，并且保留了数据的空间信息。

如果小伙伴们觉得本文对各位有帮助，欢迎：👍点赞 | ⭐ 收藏 | 🔔 关注。我将持续在专栏《人工智能》中更新人工智能知识，帮助各位小伙伴们打好扎实的理论与操作基础，欢迎🔔订阅本专栏，向AI工程师进阶！