从头认识AI-----循环神经网络（RNN）

逻辑0

于 2025-05-29 15:47:07 发布

阅读量948

点赞数 23

分类专栏：人工智能文章标签：人工智能 rnn 深度学习

本文链接：https://blog.csdn.net/weixin_48222697/article/details/148308403

版权

人工智能专栏收录该内容

15 篇文章

订阅专栏

前言

前面我们讲了传统的神经网络，如MLP、CNN，这些网络中的输入都被单独处理，没有上下文之间的信息传递机制，这在处理序列数据（如语音、文本、时间序列）时很鸡肋：

如何理解一句话中“前后文”的含义？
如何预测下一个时刻的股价？
如何让模型记住历史信息？

为了解决现实世界中的序列建模问题，循环神经网络应运而生。

一、什么是RNN?

其实RNN就是一种带有“记忆功能”的神经网络架构，它能够处理长输入序列，在每个时刻都利用前一时刻的隐藏转态作为“上下文信息”。也可以说，RNN就是一个隐变量模型，隐变量转态是一个向量，RNN做的就是如何更新这个向量。

假设现在有一条文本：“你好，明天！”，使用RNN预测下一个词，则RNN中隐变量的更新如下如所示：

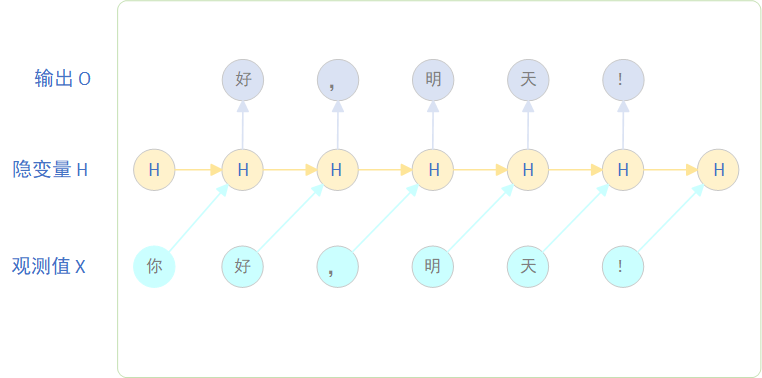
其中，前一个隐藏转态： $h_{t-1}$ ，需要当前输入： $x_t$ ，当前隐藏转态为： $h_t$

二、RNN的数学原理

其实RNN的核心公式很简单，前面我已经说过，RNN其实就是一个隐变量模型，隐变量转态是一个向量，RNN就是如何更新这个隐变量向量。

具体隐状态更新公式如下：

$H_t=tanh(W_{xh}@X_t+W_{hh}@H_{t-1}+b_h)$

$O_{t}=W_{ho}@H_t+b_o$

其中：

$W_{xh}$ ：输入到隐藏的权重
$W_{hh}$ ：隐藏到隐藏的权重
$W_{ho}$ ：隐藏到输出的权重

三、手写一个简单的RNN

我们已经知道了RNN隐转态具体的更新流程，接下来，我来手写一个最简单的RNN：

1. 初始化参数

我先初始化所需要更新的参数：

import torch

def params(input_size, output_size, hidden_size):
    W_xh = torch.randn((input_size, hidden_size)) * 0.1
    W_hh = torch.randn((hidden_size, hidden_size)) * 0.1
    b_h = torch.zeros(hidden_size)
    W_ho = torch.randn((hidden_size, output_size)) * 0.1
    b_o = torch.zeros(output_size)
    
    params = [W_xh, W_hh, b_h, W_ho, b_o]
    for param in params:
        param.requires_grad=True
    return params

2. 初始化隐藏转态

因为在0时刻时，没有隐藏转态，因此我们需要初始化一个隐藏状态：

def init_state(batch_size, hidden_size):
    return (torch.zeros((batch_size, hidden_size))

3. 隐状态更新

import torch

def rnn(X, state, params):
    W_xh, W_hh, b_h, W_ho, b_o = params
    H = state
    outputs = []
    for x in X:
        H = torch.tanh(torch.mm(x, W_xh) + torch.mm(H, W_hh) + b_h)
        O = torch.mm(H, W_ho) + b_o
        outputs.append(O)
    return torch.cat(outputs, dim=1), (H, )

4. 总的架构

接下来，将所有的模块整合在一起：

import torch
import torch.nn as nn
import torch.nn.functional as F

def params(input_size, output_size, hidden_size):
    W_xh = torch.randn((input_size, hidden_size)) * 0.1
    W_hh = torch.randn((hidden_size, hidden_size)) * 0.1
    b_h = torch.zeros(hidden_size)
    W_ho = torch.randn((hidden_size, output_size)) * 0.1
    b_o = torch.zeros(output_size)
    
    params = [W_xh, W_hh, b_h, W_ho, b_o]
    for param in params:
        param.requires_grad(True)
    return params

def init_state(batch_size, hidden_size):
    return (torch.zeros((batch_size, hidden_size))

def rnn(X, state, params):
    W_xh, W_hh, b_h, W_ho, b_o = params
    H = state
    outputs = []
    for x in X:
        H = torch.tanh(torch.mm(x, W_xh) + torch.mm(H, W_hh) + b_h)
        O = torch.mm(H, W_ho) + b_o
        outputs.append(O)
    return torch.cat(outputs, dim=1), (H, )

class myrnn(nn.Module):
    def __init__(self, input_size=None, output_size=None, hidden_size=None, params=None, init_state=None, fn=None):
        self.input_size = input_size
        self.output_size = output_size
        self.hidden_size = hidden_size
        self.params = params(self.input_size, self.output_size, self.hidden_size)
        self.init_state = init_state
        self.fn = fn
    def __call__(self, X, state):
        X = F.one_hot(X.T, self.input_size).type(torch.float32)
        return self.fn(X, state, self.params)
    def state(self, batch_size):
        return self.init_state(batch_size, self.hidden_size)

# 示例
hidden_size = 256
input_size = output_size = 10
X = torch.arange(10).reshape(2,5)
model = myrnn(input_size=input_size, output_size=output_size, hidden_size=hidden_size, params=params, init_state=init_state, fn=rnn)
state = model.state(X.shape[0])
output, new_state = model(X, state)
print(output.shape)

四、使用Pytorch实现

Pytroch中已经内置了RNN模块，在实际应用中，我们只需要调用相应的RNN即可，接下来我简单演示一下：

import torch
import torch.nn as nn

class Rnn(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Rnn, self).__init__()
        self.rnn = nn.RNN(input_size, hidden_size, batch_first=True)
        self.fc = nn.Linear(hidden_size, output_size)
    def forward(self, x, h0):
        out, hn = self.rnn(x, h0)
        out = self.fc(out)
        return out, hn
   
# 示例
model = Rnn(input_size=10, hidden_size=256, output_size=10)
x = torch.randn(1,5,10)
h0 = torch.zeros(1,1,256)
output, hn = model(x, h0)
print(output.shape, hn.shape)