基本定义
信道码可以分为两大类:分组码和卷积码。
在块码中,M = 个消息中的一个,每个消息表示一个长度为k的二进制序列,称为信息序列,映射到一个长度为n的二进制序列,称为码字,其中n > k。码字通常通过发送n个二进制符号的序列在通信信道上传输,例如,通过使用BPSK。QPSK和BFSK是经常用于码字传输的其他类型的信令方案。
分组码是无记忆性的。一个码字被编码传输后,系统接收到一组新的k个信息位,并使用编码方案定义的映射对其进行编码。产生的码字仅依赖于当前的k个信息位,与之前传输的所有码字无关。
卷积码是用有限状态机描述的。在这些码中,在每个时间实例i, k个信息位进入编码器,在编码器输出处产生n个二进制符号,使编码器的状态从变为
可能状态的集合是有限的,用表示。编码器输出产生的n个二进制符号和下一个状态
取决于输入j寄存器的kK位以及
。如图所示
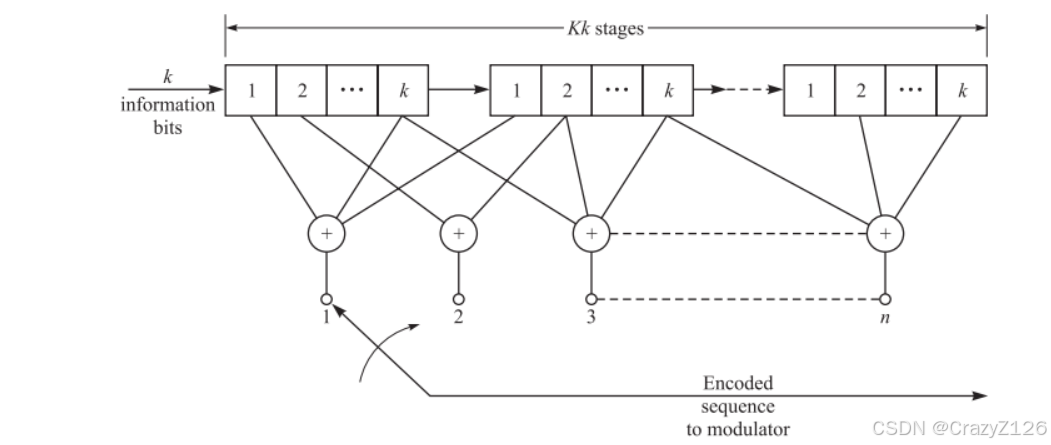
码率定义为

传输速率
长度为n的码字使用N维空间的M-ary调制,![]() 定义为每个码字传递的符号数,假设每个符号的传递时间为
定义为每个码字传递的符号数,假设每个符号的传递时间为![]() ,由此传递速率为
,由此传递速率为

假设采用最小的所需带宽进行采样(采样定理)带宽为

由此可以得到频谱效率为
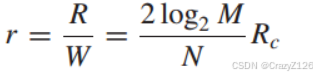
与使用相同调制方案的非编码系统相比,比特率变化了Rc倍,带宽变化了1/Rc倍,即速率降低了,带宽增加了。
从能量的角度来看
所有星座点的平均能量为![]() ,每个码字的能量为
,每个码字的能量为![]() ,由此
,由此

码字中每一个比特能量为

输入每比特的能量用Eb表示,可由

码字和输入的每比特能量关系

传输功率定义为

传输功率 = 传输每比特能量 × 每比特的速率
对于BPSK、BFSK和QPSK (N = 2,复数域?)有

有限域
对于四则运算封闭。
如果满足下列性质,则集合G和用+表示的二元运算构成Abelian组满足:
- 交换律
- 结合律
- 存在运算不变单位
- 存在运算的逆
表示为![]()
有限域或Galois field是一个有限集合F,它具有两个二元运算:加法和乘法,分别用+和·表示,满足下列性质:
- {F, +, 0}是一个Abelian组
- {F−{0},·,1}是一个Abelian 组;即,域的非零元素与单位元素“1”相乘构成一个阿贝尔群。a∈F的乘法逆记为

- 满足乘法分配率
实数集R是一个域(但不是有限域),具有普通的加法和乘法。具有模-2加法和乘法的集合F ={0,1}是GF域的一个例子。这个域称为二进制域。
有q个元素的GF域,用GF(q)表示,存在当且仅当,p是质数,m是正整数。
当q = p时,伽罗瓦场可表示为GF(p) ={0,1,2,…, p−1}与模p的加法和乘法。例如GF(5) ={0,1,2,3,4}是一个具有模5加法和乘法的有限域。
当时,得到的GF域称为GF(p)的扩展域。在这种情况下,GF(p)称为GF(
)的Groud field,p称为GF(pm)的特性
.
有限域的多项式
为了研究扩展域的结构,我们需要定义GF(p)上的多项式

多项式的加法和乘法遵循普通多项式的标准加法和乘法规则,只是系数的加法和乘法是模p的。
如果一个m次多项式在GF(p)上不能写成同一个GF域上两个较低次多项式的乘积,则该多项式称为不可约多项式。
![]() 在GF(2)上是一个不可约的多项式,
在GF(2)上是一个不可约的多项式,![]() 是可约的。
是可约的。
代数的一个基本结果表明,次数为m 的GF(p)的多项式有m个根(有些可以重复),但根不一定在GF(p)中。一般情况下,根在GF(p)的扩展域中。
扩展域的结构
从上述定义可以清楚地看出,存在个多项式次数小于m;特别地,这些多项式包括两个特殊的多项式g(X) = 0和g(X) = 1。现在让我们假设g(X)是一个m次的素数(一元不可约)多项式,并考虑所有次数小于m 在 GF(p)的多项式的集合,这些多项式具有原来的加法和多项式乘法模g(X)。可以证明,这些多项式的加法和乘法运算的集合是一个有
个元素的GF域。
例子
我们知道![]() 是素数多项式在GF(2)。因此,这个多项式可以用来构造GF(
是素数多项式在GF(2)。因此,这个多项式可以用来构造GF() = GF(4)。让我们考虑所有次数小于2 的。这些多项式是0、1、X和X + 1,其加法和乘法表所示。注意,乘法法则基本上需要将两个多项式相乘,将乘积除以g(X) =
![]() ,然后求余数。这就是模g(X)相乘的意思。有趣的是,GF(4)的所有非零元素都可以写成X的幂;即
,然后求余数。这就是模g(X)相乘的意思。有趣的是,GF(4)的所有非零元素都可以写成X的幂;即![]() (这是通过除以g(X)取余得到的 )
(这是通过除以g(X)取余得到的 )

乘法计算过程
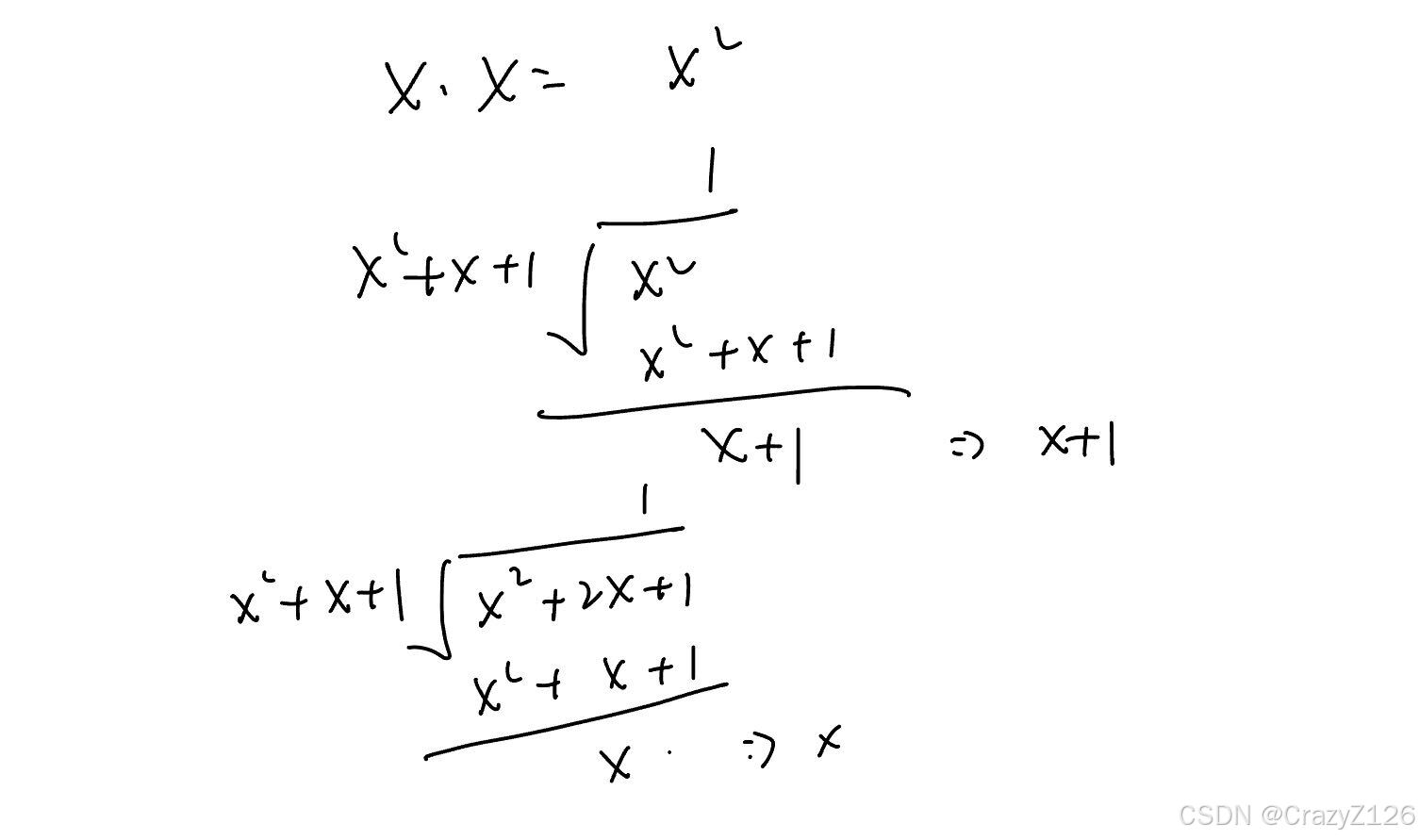
为了生成GF(),我们可以使用两个素数多项式g1(X) =
![]() 或g2(X) =
或g2(X) = ![]() 中的任何一个。若取g(X) =
中的任何一个。若取g(X) =![]() ,
,


初元素和初多项式
定义:对于任何一个在GF(q)域中的非零值β,都满足的i的值成为β的order(序数)。显然在GF(q)域中有
,因此β的序数最大不会有q-1.
初元素(primitive element)定义为他们的次数能构成GF域中所有的非零值,序数为q-1.。
对于最大次数为m的多项式中,有许多素数多项式。
对于一个GF(),如果是由g(x)生成的话,同时X是这个域的初元素,这这个生成多项式g(x)是初多项式。
例题:

因为,所以第二个多项式不是素数多项式。
初多项式的第二个判断准则:
对于一个在GF(p) 的自由度为m(最高次为)多项式,则一定可以被多项式
整除。但同时可能存在可以
被整除。如果不存在比
小的i使得上述式子成立,这个素数多项式是初多项式。
例题


上述例子给出由多项式g(x)域中的所有非零值中的所有初元素。
最小多项式和共轭元素
如果β是GF()中的非零元素,对于β的最小多项式
,定义为在GF(2)中满足
.
显然是一个素数多项式。
反证法
假设是最小多项式但是不是一个素数多项式,则
= a(X)b(X),若a(X) 和b(X)的根都为β,则
不是最小多项式,若只有一个根为β,同样不是最小多项式。证毕
所以对于GF(2)上的所有多项式f(x), 如果f(β) = 0, 则一定可以表示是f(X) = a(X) 。
寻找最小多项式
对于β是GF()中的非零元素,有
同时可能存在一些l <m 使得
成立.所以最小多项式可以表示如下的形式

l是成立的最小的整数,
其中![]() 是多项式的
是多项式的![]() 的根,同时成为β的共轭,这些元素有着相同的序数。这意味着初元素的共轭依旧是初元素。
的根,同时成为β的共轭,这些元素有着相同的序数。这意味着初元素的共轭依旧是初元素。
例子:



 最后两个都是初元素,但是他们属于不同的共轭类,所以他们有不同最小多项式。
最后两个都是初元素,但是他们属于不同的共轭类,所以他们有不同最小多项式。
矢量空间
性质

线性分组码的一般性质
线性分组码C是n维空间的一个k维子空间,通常称为(n,k)码对于二进制码,线性分组码是长度为n的2k个二进制序列的集合,使得对于任意两个码字 C1,C2,我们有C1+c2也属于这个线性分组码的集合。显然,0是任何线性分组码的码字。
生成矩阵和奇偶校验矩阵
G表示生成矩阵,u为输序列,c为输出码字。
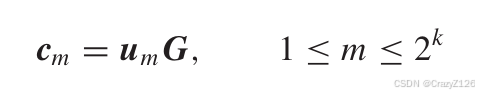
生成矩阵表示为向量

输出码字为

系统的生成矩阵

码字存在纯在互补空间满足:

等价于

所以

对于二进制码

所以

例题:
生成矩阵

校验矩阵


线性分组码的权重和距离
一个码子的权重表示一个码字的所有非零值个数。
码字的最小距离定义为
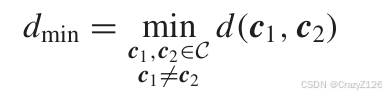
最小权重等于最小距离

最小权重和奇偶校验矩阵的列的关系
对于一个码字满足

对于另外一个码字也满足

因为两个码字的最小权重为d,所以H最少有d个线性相关的列向量。
欧式距离和最小汉明距离的关系:
BPSK
每个码字的输出符号表示为

因此两个不同的符号之间的欧氏距离为

于是

权重分布多项式
权重枚举函数

![]() 表示权重为i的码子的个数。
表示权重为i的码子的个数。
Z取1表示把所有的权重的码字全部计算上

Z取0表示只计算权重为0的码字。

权重枚举函数和对偶码的权重枚举函数之间的关系为

码的权值枚举函数与星座的距离枚举函数密切相关
BPSK
![]()
BPSK的距离枚举函数

输入-输出权重枚举函数

![]() 为权重为j的信息序列生成的权重为I的码字个数
为权重为j的信息序列生成的权重为I的码字个数
多项式Y的次数对应输入的权重,Z的次数对应输出的权重,前面的系数为权重变换对应的次数。
类似全概率公式

由于系数关系当Y=1 的时候有

条件权重函数conditional weight enumeration function (CWEF)

表示权重为j的信息序列所对应的所有码字的权重枚举函数。
条件枚举函数和输入输出的权重枚举函数关系(类似留数定理的推导)
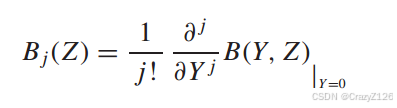
线性分组码的错误概率
块错误概率
线性码的线性保证了一个码字到所有其他码字的距离与码字的选择无关。因此,在不丧失一般性的情况下,我们可以假设传输的是全零码字。
易错成![]() 的概率为
的概率为![]()
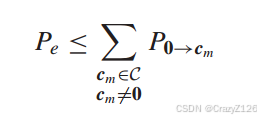
因为对于同等权重的码字,我们有相同的![]() 于是有
于是有

![]() 表示成对错误概率(pairwise error probability),假设码字PEP有
表示成对错误概率(pairwise error probability),假设码字PEP有

定义每一位的易错概率为
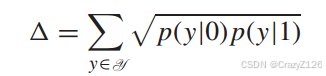
码字等效为权重有:

待会权重求和

利用权重枚举函数

放缩
由于不等式

得到


放缩次数得到

比特错误概率
我们再次假设传输的是全零序列;则权重为i的特定码字在检测器处被解码的概率等于![]() 。
。
![]() 表示权重为i的码字个数对应权重为j的信息序列的对应个数。
表示权重为i的码字个数对应权重为j的信息序列的对应个数。
因此,当传输全0时,期望接收到的错误信息位数

第二个求和表示译成权重为i并且此时对应的输入的码字权重为j的概率,前面求和表示这个时候的差错比特数。
放缩(增加了一些0项)

因此,当传输0时,误码接收信息的期望比特数为:线性分组码Pb的(平均)误码概率定义为误码接收信息的期望比特数与总传输比特数之比,

第二项为条件枚举函数(![]() ),所以有
),所以有

利用
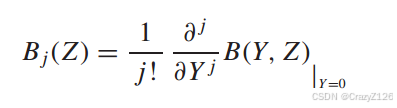
有
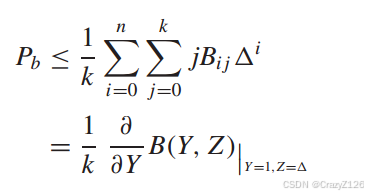
一些特殊的线性分组码
重复编码
二进制重复码是一个(n, 1)码,两个码字长度为n.
一个码字是全零码字,另一个是全一码字。
这个码的速率![]() ,最小距离
,最小距离![]()
重复码的对偶是一个(n, n−1)码,由所有长度为n且偶校验的二进制序列组成。双码的最小距离显然是![]() (对偶码的校验矩阵是重复码的全1生成矩阵)。
(对偶码的校验矩阵是重复码的全1生成矩阵)。
汉明码
汉明码是参数![]() ,
,![]() 的线性分组码(m≥3)m等于1的时候是重复编码。
的线性分组码(m≥3)m等于1的时候是重复编码。
汉明码最好用奇偶校验矩阵来描述H是一个![]() 矩阵。
矩阵。
H的![]() 列由所有可能的长度为m的二进制向量组成,不包括全零向量。(特点)
列由所有可能的长度为m的二进制向量组成,不包括全零向量。(特点)
汉明码的码率为

因为H的列包含了所有长度为m的非零序列,所以任意两列的和是另一列(一个线性码的求和还在这个空间)。所以
![]()
权重分布多项式

例子:
(7,4)汉明码生成矩阵

最大长度码
最大长度码是汉明码的对偶,这些是m≥3的![]() 码族。
码族。
最大长度码的生成矩阵是汉明码的奇偶校验矩阵。
所以生成矩阵的所有列都是长度为m的序列,除了全零序列。
最大长度码是等权码,这个权重等于![]() 所以对应的权重枚举函数为
所以对应的权重枚举函数为

由此可以得到汉明码的枚举函数
Reed-Muller码
一类具有灵活参数的线性分组码,由于存在简单的解码算法而特别有趣。
码长n,级数r,输入码长k,最小距离满足下列关系:

生成矩阵

第一个矩阵全1

第二个矩阵的每一列对应长度为m的所有二进制码

后面的比较复杂(略过)
例子
(8, 4)RM码

阿达马码(Hadamard)码
通过选择阿达玛矩阵的行作为码字来获得阿达玛码。
阿达玛矩阵Mn是一个由1和0组成的n × n矩阵(n是一个偶数),它的性质是任意一行与其他行相差正好n个位置。†矩阵的一行包含所有0。其他行各包含n个0和n个1。
例如n = 2,

对于高阶

![]() 表示补码(0被1替换,反之亦然)
表示补码(0被1替换,反之亦然)![]()
所以


性质:
![]()
线性分组码的最优软判决解码
我们知道,在最小化码字错误平均概率的意义上,AWGN信道的最佳接收器可以实现为与M个可能的发射波形相匹配的![]() 滤波器的并行组。
滤波器的并行组。
比较每个信令间隔结束时M个匹配滤波器的输出,其中包含码字中n个二进制符号的传输,并选择最大匹配滤波器输出对应的码字。
![]() 表示匹配滤波器对任何特定码字的n个采样输出,由于信号是二进制相干PSK,输出rj可以表示为:
表示匹配滤波器对任何特定码字的n个采样输出,由于信号是二进制相干PSK,输出rj可以表示为:
当码字的第j位是1时
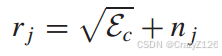
当码字的第j位是0时
![]()
最佳解码器形成M个相关度量

![]() 表示第m位码字的第j位。.
表示第m位码字的第j位。.
因此,若![]() ,则权重因子
,则权重因子![]() ;如果
;如果![]() ,则权重因子
,则权重因子![]() 。这样,加权
。这样,加权![]() 将{rj}中的信号分量对齐,使得与实际传输码字对应的相关度量将具有平均值
将{rj}中的信号分量对齐,使得与实际传输码字对应的相关度量将具有平均值![]() ,而其他M−1度量将具有较小的平均值。
,而其他M−1度量将具有较小的平均值。
对于码字数目较大,这可能不切实际例如![]()
块误码率和比特误码率
BPSK有
![]()
因此有
![]()
误码率有
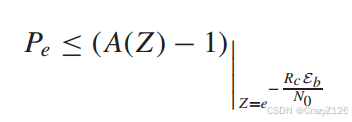
放缩

利用不等式有![]()

对于无编码BPSK有误码上界![]() ,
,
由此可以得到编码增益为![]() 。
。
对于比特误码率可以计算为

软译码非相关检测
FSK的非相关检测

相关矩阵为


两个相关度量的差为

误码上界




带宽关系
当使用二进制PSK传输每个比特时,传输编码波形所需的信道带宽由式给出

无编码BPSK方案的带宽要求为R。因此,带宽扩展系数

和正交信号对比
与BPSK信号相比,正交信号更节能,但使用正交信号需要更大的带宽。
我们还看到,使用编码BPSK信号导致带宽适度扩展,同时,通过提供编码增益,提高了系统的功率效率。
让我们考虑两个系统,一个采用正交信号,另一个采用编码BPSK信号来实现相同的性能。
对于正交误码性能

对于编码误码性能

两者一样性能下,输入的比特长度满足![]() ,每个比特正交下需要维度
,每个比特正交下需要维度![]() 。计算为
。计算为![]()
BPSK码波形的维数![]() (输出的波形的比特数)
(输出的波形的比特数)

假设我们使用最小距离为dmin = 13的(63,30)二进制码。相对于此代码,正交信令的带宽比大致为205。换句话说,执行类似于(63,30)码的正交信令方案需要编码系统带宽的205倍。这个例子清楚地显示了编码系统的带宽效率。
线性分组码的硬解码
软解码是采样点没有进行量化的结果。虽然这种处理产生了最好的性能,但基本的限制是形成M个相关指标并比较这些指标以获得最大的计算负担。
为了减少计算量,可以对模拟样本进行量化,然后对解码操作进行数字化处理。
在本节中,我们考虑一种极端情况,即对应于码字的单个比特的每个样本被量化为两个级别:0和1。
AWGN信道下,(调制器/解调器)构成一个交叉概率为p的BSC。对于PSK

最小距离译码(ML)
接收到的码字相对应的来自检测器的n位被传递到解码器,h将接收到的码字与M个可能传输的码字进行比较,选择汉明距离中最接近的码字。
这种最小距离解码规则是最优的,因为它导致二进制对称信道的码字错误概率最小。
所有M个可能传输的码字![]() ,以获得误差向量
,以获得误差向量![]() ,
,![]() 表示为了转换码字为特定接收码字上发生的错误。转换为接收到的码字时的错误数正好等于
表示为了转换码字为特定接收码字上发生的错误。转换为接收到的码字时的错误数正好等于![]() 中1的个数,简单地计算M个误差向量
中1的个数,简单地计算M个误差向量
{![]() }的权重,并决定选择产生最小权重误差向量的码字,就是最小距离译码规则的实现。
}的权重,并决定选择产生最小权重误差向量的码字,就是最小距离译码规则的实现。
标准差错阵列
一种更有效的硬判决解码方法是利用奇偶校验矩阵。
![]() 为发射码字,
为发射码字,![]() 为探测器输出端的接收序列,
为探测器输出端的接收序列,![]() 表示任意二进制误差向量。有
表示任意二进制误差向量。有
![]()
和

(n−k)维向量![]() 表示差错模式。向量s的分量对于所有满足的奇偶校验方程为零,对于所有不满足的奇偶校验方程为非零。
表示差错模式。向量s的分量对于所有满足的奇偶校验方程为零,对于所有不满足的奇偶校验方程为非零。
如果s等于零,在这种情况下,我们有一个未检测到的错误(y是原来的码字空间的码字)。
如果s不等于零,这种情况下,有一个错误模式(向量e)没有被检测到。
因此所有的![]() 接受差错模式(全零序列不算作错误),
接受差错模式(全零序列不算作错误),![]() 个是无法被检测(收到啥就是啥)。
个是无法被检测(收到啥就是啥)。![]() 可以检测到非零错误模式,但并非所有错误模式都可以纠正。
可以检测到非零错误模式,但并非所有错误模式都可以纠正。
因为接受向量维度为n-k,所以只有![]() 个可以纠错的错误模式。
个可以纠错的错误模式。
标准差错阵列

例子,如何使用差错模式和标准差错阵列
(5,2)线性码生成矩阵


最小距离![]() ,
,
尽管存在更多的双重错误模式,但只允许两种错误模式完成该表(后面的不要了,因为这个表放不下去列数受最小距离限制,两个模式的错误也有可能和一个错误的有一样的s)
当接受序列表示为

内积之后有

相同的e对应的s相同。
对接收到的序列y进行解码的过程基本上就是找到最小权值的错误序列![]() ,
,![]()
通过在y加上![]() (等效于减)就可以得到最有可能的传送码字。
(等效于减)就可以得到最有可能的传送码字。
例子:接上个例子有

假设出错为

计算得到
![]()
对应的译码差错序列
![]()
依旧有错。
换句话说,(5,2)代码纠正了所有单错误和两个双错误,即(1 1 0 0 0)和(1 0 0 1 0)。
差错检测能力和差错纠错能力
从上面的讨论可以清楚地看出,当s由全零组成时,所接收的码字是个可能的![]() 传输码字之一。因为码字之间的最小间隔是
传输码字之一。因为码字之间的最小间隔是![]() ,可能将代码中的这
,可能将代码中的这![]() 个码字中的一个转换为另一个码字(至少发生
个码字中的一个转换为另一个码字(至少发生![]() 位比特错误)。当发生这种情况时,我们有一个未检测到的错误。另一方面,如果实际误差数小于最小值
位比特错误)。当发生这种情况时,我们有一个未检测到的错误。另一方面,如果实际误差数小于最小值![]() (说明检测的一定不是输出的码字集合中的一个),s会有非零值。当出现这种情况时,我们已经检测到通道上存在一个或多个错误。
(说明检测的一定不是输出的码字集合中的一个),s会有非零值。当出现这种情况时,我们已经检测到通道上存在一个或多个错误。
(n, k)块码能够检测到![]() 的错误。
的错误。
码的纠错能力也取决于最小距离,可纠正错误模式的数量受限于标准数组中每一列的数量。
为了确定(n, k)码的纠错能力,可以方便地将![]() 个码字视为n维空间中的点。如果将每个码字视为半径为(汉明距离)t的球体的中心,没有交集的情况下t可能具有的最大值
个码字视为n维空间中的点。如果将每个码字视为半径为(汉明距离)t的球体的中心,没有交集的情况下t可能具有的最大值![]()
在每个球内存放距离有效码字小于等于t的所有可能接收码字。因此,任何落在球体内的接收代码向量都被解码为球体中心的有效码字。
距离最小的(n, k)码具有纠错能力![]()
显然,纠正t个错误意味着我们已经检测到t个错误。然而,如果我们牺牲了代码的纠错能力,也有可能检测到超过t个错误。
对于![]() 的(n,k)码能最多修正3个错误。 如果我们希望检测四个错误,我们可以通过将每个码字周围的球体半径从3减小到2来实现,因此,具有四个错误的模式是可检测的,但只有两个错误的模式是可纠正的。(当把半径减小到2时候,发送一个码字,当接受码字距离这个码字的
的(n,k)码能最多修正3个错误。 如果我们希望检测四个错误,我们可以通过将每个码字周围的球体半径从3减小到2来实现,因此,具有四个错误的模式是可检测的,但只有两个错误的模式是可纠正的。(当把半径减小到2时候,发送一个码字,当接受码字距离这个码字的的时候这个时候一定是知道有错的,如果发生
以上的错误的时候,由于进入了其他的码字的纠错区域,会被自动纠错成其他码字而不认为出错,所以就无法无法检测出出错)。
所以有检错能力![]() 和纠错能力
和纠错能力![]() 满足
满足
![]()
和


硬解码的块误码率和比特误码率
检错能力

由于二进制对称信道是无内存的,因此位错误是独立发生的。因此,在n位块中出现m个错误的概率为

因此块误码率为

高信噪比,p值很小,由p的最小次数决定块误码率

对于比特误码率,我们注意到,如果发送0,接收权值为t + 1的序列。解码器会将接受序列译成距离接收序列最多为t的码字,这意味着对于最优可能的块出错有2t + 1位错误。所以
 (高信噪比)
(高信噪比)
最优码
假设我们在每个可能传输的码字周围放置一个半径为t的球体,码字周围的每个球包含到码字汉明距离小于等于t的所有码字的集合。一个球体中码字的数目

![]() 可能传输的码字,
可能传输的码字,![]() 不重叠的球,每个球的半径为t。
不重叠的球,每个球的半径为t。![]() 个球中包含的码字总数不能超过
个球中包含的码字总数不能超过![]() 个可能接收到的码字。所以纠错能力为t的码必须满足不等式
个可能接收到的码字。所以纠错能力为t的码必须满足不等式
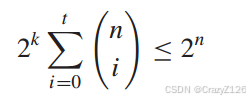
等效于

对于这样的码,权重小于或等于t的所有错误模式都由最佳(最小距离)解码器纠正。另一方面,任何权重为t + 1或更大的错误模式都不能被纠正。
准最优码
M个可能传输码字周围的汉明半径为t的所有球都是不相交的,并且每个接收码字与其中一个可能传输码字的距离最多为t +1。所有权值小于或等于t的误差模式和一些权值为t + 1的误差模式都是可修正的。有块误码率

球外的码字总数为

平均每一个球可以扩大的区域有

因此,在与每个码字的距离为t+1的![]() 错误模式中,我们可以纠正
错误模式中,我们可以纠正![]() 个错误模式。
个错误模式。
于是准最优码的块误码率

从最小距离的角度,块误码率大于将传输的码字错误地解码为其最近邻居的概率

上界译成其他所有的码字的概率

从权重枚举函数来看如果![]() 则有
则有

























 1152
1152

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








