P6510 奶牛排队(单调栈+二分)

最新推荐文章于 2024-10-28 14:12:21 发布

原创最新推荐文章于 2024-10-28 14:12:21 发布 · 891 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#c语言

单调队列/单调栈同时被 2 个专栏收录

7 篇文章

订阅专栏

数据结构与算法

7 篇文章

订阅专栏

本文解析了一道关于奶牛排队的问题，利用单调栈技巧解决A作为左矮点、B为右高点且中间无相同身高奶牛的条件，通过双栈维护找到符合条件的最大奶牛数量。关键在于借助单调性找到A点，以及使用数组模拟栈实现高效操作。

P6510 奶牛排队
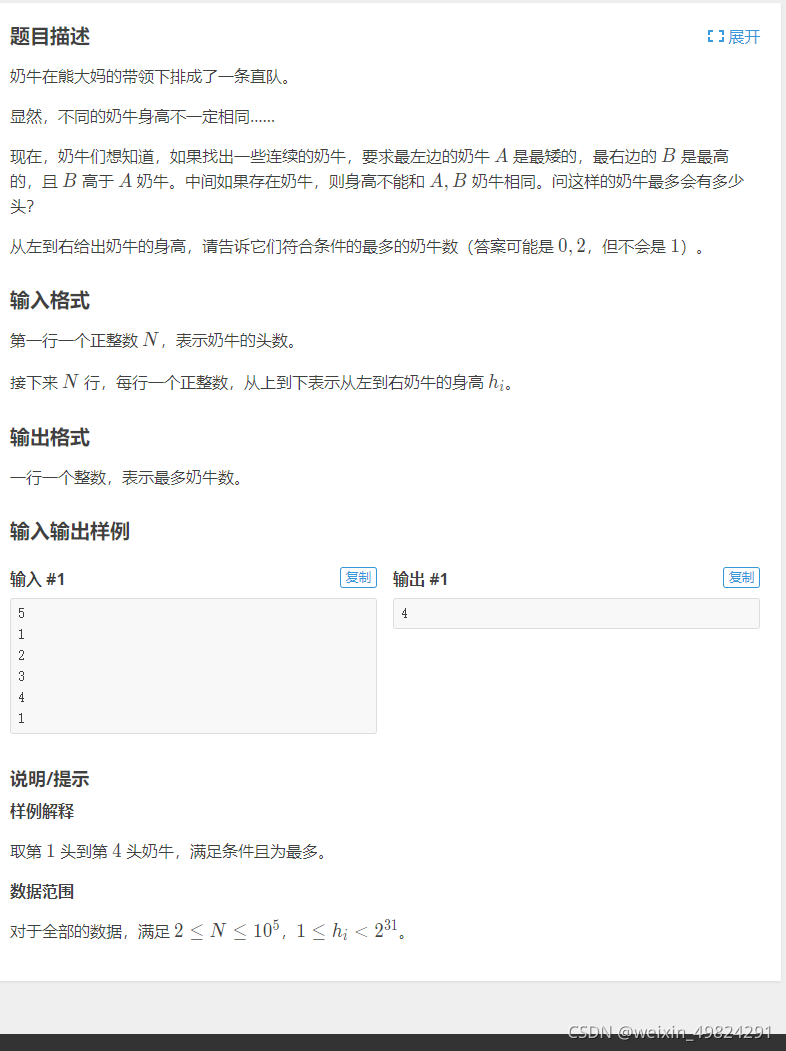
在这里插入图片描述
该题要求找出符合条件的最多奶牛数,条件是A作为左端点最矮,B作为右端点最高,中间不能有与A,B相同身高的奶牛,枚举每个端点作为预备B端点,则A端点一定在左边比B端点高的奶牛的后面,也就是找到左边第一个比该点大的数,这个可以用单调栈完成,这个点暂时称为X点,接下来,找A端点,A的条件是在A-B之间没有比它矮的,也就是X-B之间最小的点,该点到B的距离为最长,难点来了,如何维护呢,看完别人的题解才知道,可以用俩个单调栈来维护,通过单调递减栈找到左边第一个大于B的点x,而如何找到x点与B点中最小的点呢,用单调递增栈只能维护从1开始的最小值,妙处在于栈里存的是下标,对该栈二分搜索找到第一个大于x点下标的点,该点就是A点了.另外学到了可以用数组模拟栈.

#include<bits/stdc++.h>
using namespace std;

#define int long long
int sx[100005],sn[100005],a[100005];
signed main(){
	int n;
	scanf("%lld",&n);
	for(int i=1;i<=n;i++){
		scanf("%lld",&a[i]);
	}
	int tn=0,tx=0,ans=-1;
	for(int i=1;i<=n;i++){
		while(tx!=0&&a[sx[tx]]<a[i]){
			tx--;
		}
		while(tn!=0&&a[sn[tn]]>=a[i]){
			tn--;
		}
//		if(sx[tx]<i-1){
		int k;
		k=upper_bound(sn+1,sn+tn+1,sx[tx])-sn;
		if(k!=tn+1)ans=max(ans,i-sn[k]+1);
		
		sx[++tx]=i;
		sn[++tn]=i;
	}
	printf("%lld\n",ans);
	return 0;
}