棋盘覆盖问题[算法设计与分析]

实验问题：

用缺了一个格子的正方形去覆盖一个n*n的棋盘，问需要多少个才能覆盖全部棋盘

问题分析：

第一步：可以将棋盘平分为4个象限，然后判定残缺位置落在哪个象限内。

第二步：去填充中间的四个方块中的三个，残缺位置所处的象限的方块不填充。那么问题就转化为四个相同性质的子问题

第三步：顺序处理四个象限，递归实现

数学建模：

建立函数Triomino（r，c，i，j，n） 其中（r，c）是每个象限第一个点，（i，j）是残缺点的坐标，n是棋盘的规模。

第一步：找一个基准格子坐标（n/2,n/2）

判断残缺位置坐标：(i，j)与（r+n/2,c+n/2）关系确定残缺位置所处的象限。

第二步：覆盖中间四个格子中的三个。

第三步：递归顺序处理四个象限，递归出口时棋盘规模小于2

实验代码：

//棋盘覆盖问题
#define _CRT_SECURE_NO_WARNINGS

#include<stdio.h>
#include<iostream>

using namespace std;

int amo = 0;
int a[100][100] = {0};

using namespace std;

void Triomino(int r,int c,int i, int j, int n) {
	int set = 0;
	if (n < 2) {
		return;
	}
	amo += 1;
	set = amo;
	//划分
	//找到一个基准格子
	int p = n / 2;
	//填充数
	//判断缺省位置在划分区域哪个位置并覆盖中心
	//第一象限
	if (i < r + p && j < c + p) {
		//先覆盖给定的缺陷
		a[r + p - 1][c + p] = set;
		a[r + p][c + p - 1] = set;
		a[r + p][c + p] = set;
		Triomino(r, c, i, j, p);
		Triomino(r, c + p, r + p - 1, c + p, p);
		Triomino(r + p, c, r + p, c + p - 1, p);
		Triomino(r + p, c + p, r + p, c + p, p);
	}
	//第二象限
	else if (i < r + p && j >= c + p) {
		a[r + p - 1][c + p - 1] = set;
		a[r + p][c + p - 1] = set;
		a[r + p][c + p] = set;
		Triomino(r, c + p, i, j, p);
		Triomino(r, c, r + p - 1, c + p - 1, p);
		Triomino(r + p, c, r + p, c + p - 1, p);
		Triomino(r + p, c + p, r + p, c + p, p);
	}
	//第三象限
	else if (i >= r + p && j < c+p) {
		a[r + p - 1][c + p - 1] = set;
		a[r + p - 1][c + p] = set;
		a[r + p][c + p] = set;
		Triomino(r + p, c, i, j, p);
		Triomino(r, c, r + p - 1, c + p - 1, p);
		Triomino(r, c + p, r + p - 1, c + p, p);
		Triomino(r + p, c + p, r + p, c + p, p);
	}
	//第四象限
	else if(i>=r+p&&j>=c+p){
		a[r + p - 1][c + p - 1] = set;
		a[r + p][c + p - 1] = set;
		a[r + p - 1][c + p] = set;
		Triomino(r + p, c + p, i, j, p);
		Triomino(r, c, r + p - 1, c + p - 1,p);
		Triomino(r, c + p, r + p, c + p - 1,p);
		Triomino(r + p, c, r + p - 1, c + p,p);
	}
}

void print(int n) {
	int i = 0;
	int j = 0;
	for (i = 0;i < n;i++) {
		for (j = 0;j < n;j++) {
			cout << a[i][j] << "\t";
		}
		cout << '\n';
	}
}

int main() {
	int n = 0;
	int i = 0;
	int j = 0;
	cout << "请输入棋盘规模大小:";
	cin >> n;
	cout << "请输入初始棋盘残缺位置坐标:" ;
	cin >> i >> j;
	Triomino(0, 0, i, j, n);
	cout << "填充结果:" << endl;
	print(n);
	system("pause");
	return 0;
}

实验结果：

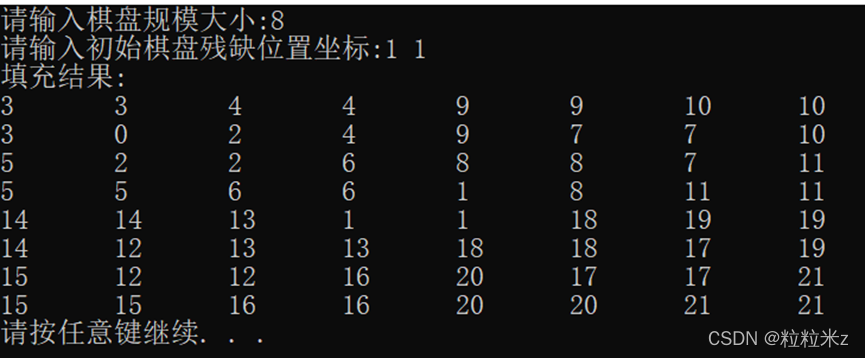
<数字代表覆盖的顺序>

时间复杂度分析： 

当k=0时T（k）=O（1）

当k>0时T（k）=4T（k-1）+O（1）即四个象限以及中间四个格子的覆盖

时间复杂度为O（）