PAT 1135 Is It A Red-Black Tree

1135 Is It A Red-Black Tree

There is a kind of balanced binary search tree named red-black tree in the data structure. It has the following 5 properties:

• (1) Every node is either red or black.
• (2) The root is black.
• (3) Every leaf (NULL) is black.
• (4) If a node is red, then both its children are black.
• (5) For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.

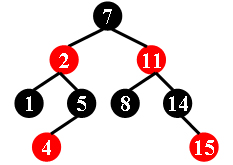
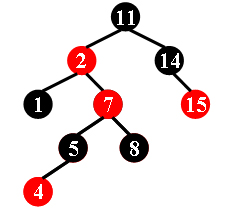
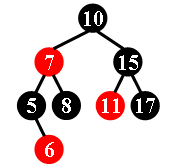
For example, the tree in Figure 1 is a red-black tree, while the ones in Figure 2 and 3 are not.

Figure 1	Figure 2	Figure 3

For each given binary search tree, you are supposed to tell if it is a legal red-black tree.

Input Specification:

Each input file contains several test cases. The first line gives a positive integer K (≤30) which is the total number of cases. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the preorder traversal sequence of the tree. While all the keys in a tree are positive integers, we use negative signs to represent red nodes. All the numbers in a line are separated by a space. The sample input cases correspond to the trees shown in Figure 1, 2 and 3.

Output Specification:

For each test case, print in a line "Yes" if the given tree is a red-black tree, or "No" if not.

Sample Input:

3
9
7 -2 1 5 -4 -11 8 14 -15
9
11 -2 1 -7 5 -4 8 14 -15
8
10 -7 5 -6 8 15 -11 17

Sample Output:

Yes
No
No

总结：这道题目是真的不会做，还是多写题目，多总结，多见识！

代码：

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
vector<int> arr;
struct node {
    int val;
    struct node *left, *right;
};
node* build(node *root, int v) {
    if(root == NULL) {
        root = new node();
        root->val = v;
        root->left = root->right = NULL;
    } else if(abs(v) <= abs(root->val))//小于等于当前节点的值，则在左边建树
        root->left = build(root->left, v);
    else
        root->right = build(root->right, v);
    return root;
}
bool judge1(node *root) {
    if (root == NULL) return true;
    if (root->val < 0) {//如果当前节点是红色，如果左右两个节点也是红色，则返回false
        if (root->left != NULL && root->left->val < 0) return false;
        if (root->right != NULL && root->right->val < 0) return false;
    }
    return judge1(root->left) && judge1(root->right);//两个子节点都要满足条件才算满足条件
}
int getNum(node *root) {
    if (root == NULL) return 0;
    int l = getNum(root->left);
    int r = getNum(root->right);
    return root->val > 0 ? max(l, r) + 1 : max(l, r);
}
bool judge2(node *root) {//从根节点开始判断，统计每个子树的到叶节点路径中黑色节点的个数是否相同
    if (root == NULL) return true;
    int l = getNum(root->left);
    int r = getNum(root->right);
    if(l != r) return false;
    return judge2(root->left) && judge2(root->right);
}
int main() {
    int k, n;
    scanf("%d", &k);
    for (int i = 0; i < k; i++) {
        scanf("%d", &n);
        arr.resize(n);
        node *root = NULL;
        for (int j = 0; j < n; j++) {//建树
            scanf("%d", &arr[j]);
            root = build(root, arr[j]);
        }
        //判断情况：①：根节点是否是黑色的 ②：红色节点后面是否跟着两个黑色节点 ③：任意一个节点到任意子代叶子节点路径中黑色节点的数量是否相同
        if (arr[0] < 0 || judge1(root) == false || judge2(root) == false)//判断该树是否是红黑树
            printf("No\n");
        else
            printf("Yes\n");
    }
    return 0;
}

 好好学习，天天向上！

我要考研！