文章目录
碎碎念
考完了,来补充一下,很多原题,不要担心。
【自我感觉这是我写的最好的一份复习笔记,希望各位学弟学妹不要浪费学姐的一份心意,好好利用,别挂科!】
y1s1,这课前面证明那块(设断言)真玄学。
【算了,是我笨蛋,学得那么费劲一定是我的问题】
【不保证没有问题,欢迎指正!】
(给后面届的学生:复习资料里有一些平时的作业题,写作业的时候别抄,认真写,认真理解)

【灵文灵文百事通!保佑我的形式化!】
考试大纲
大纲部分取自老师给的文档
(简答题我附上了答案,应用和分析证明详细看后面)
简答题
-
串行系统的程序正确性定义。
Q表示一段串行程序,X是Q的输入,Z是Q的输出,且Q合法的的输入由φ(X)来约束,合法的输出由ψ(X,Z)来约束,则称Q具有:

-
有限状态机的不足之处。(简化了一下ppt的内容)
- 本身状态图的状态数就很多,状态图复合后状态数成几何倍数增加,即使是简单的状态机多次复合后规模也很庞大。
- 有限状态机每一时刻只有一个状态可以激活,无法描述并发的情况。
- 不能描述无限状态的系统。
- 状态节点间不具备结构信息,不能清晰分辨各模块。

-
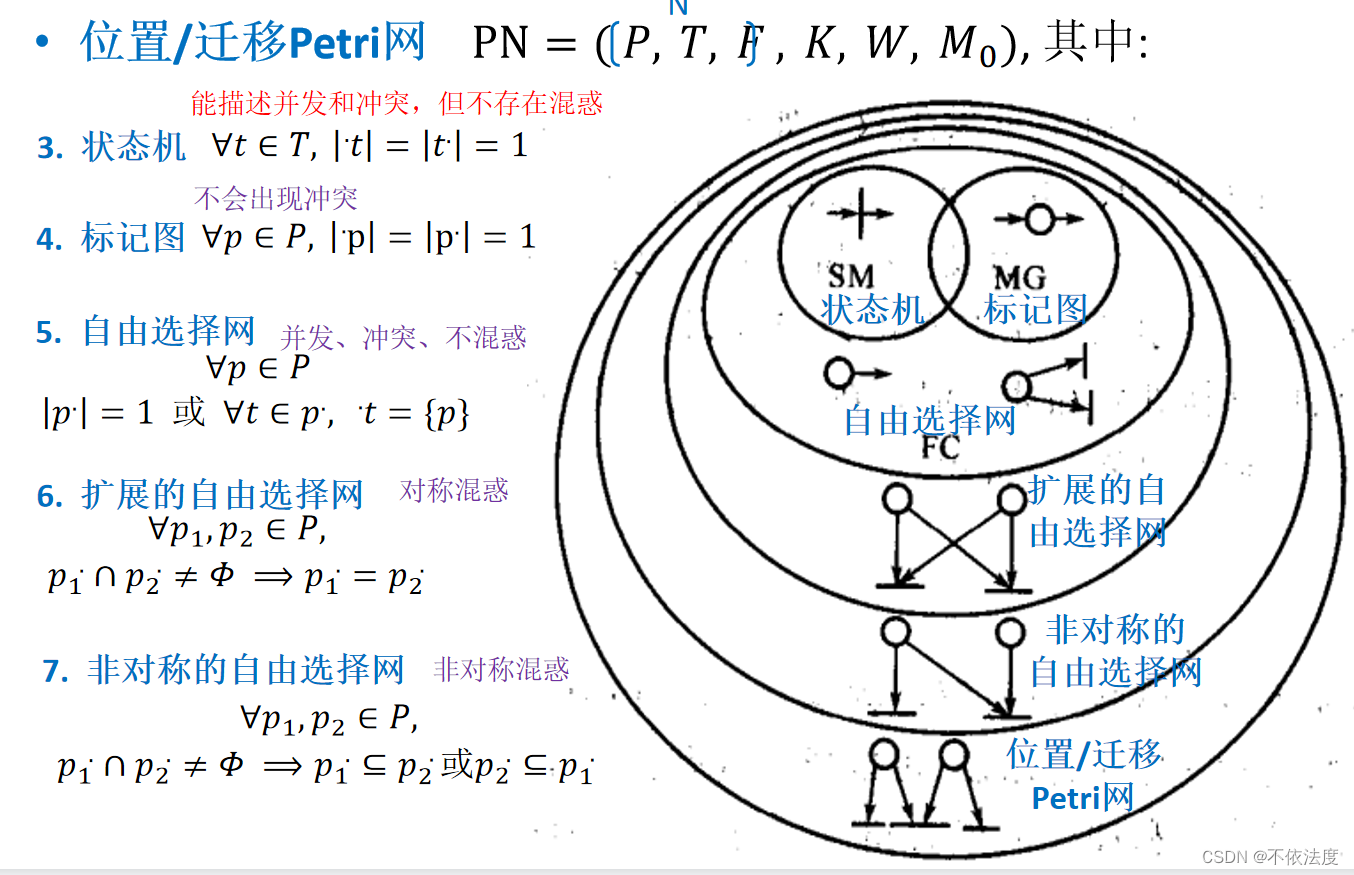
【考了】Petri 网模型上迁移间的关系(把对应的含义,例子也写出来)、几种特殊 Petri 网对各类关系的描述能力。
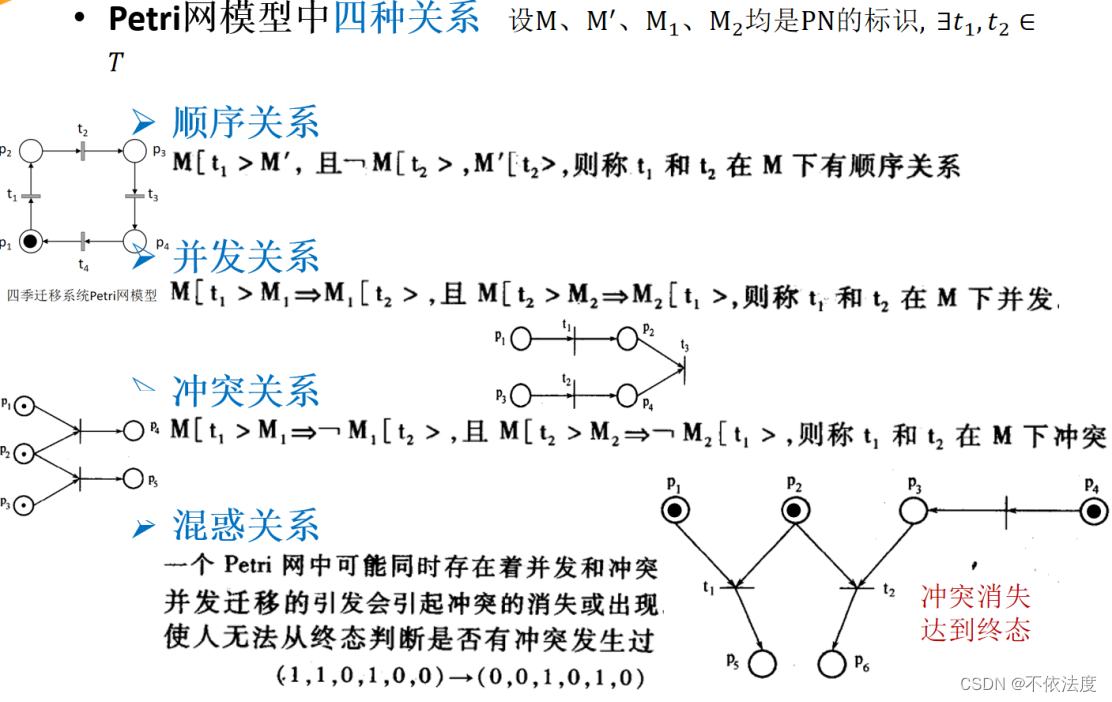

特殊petri网
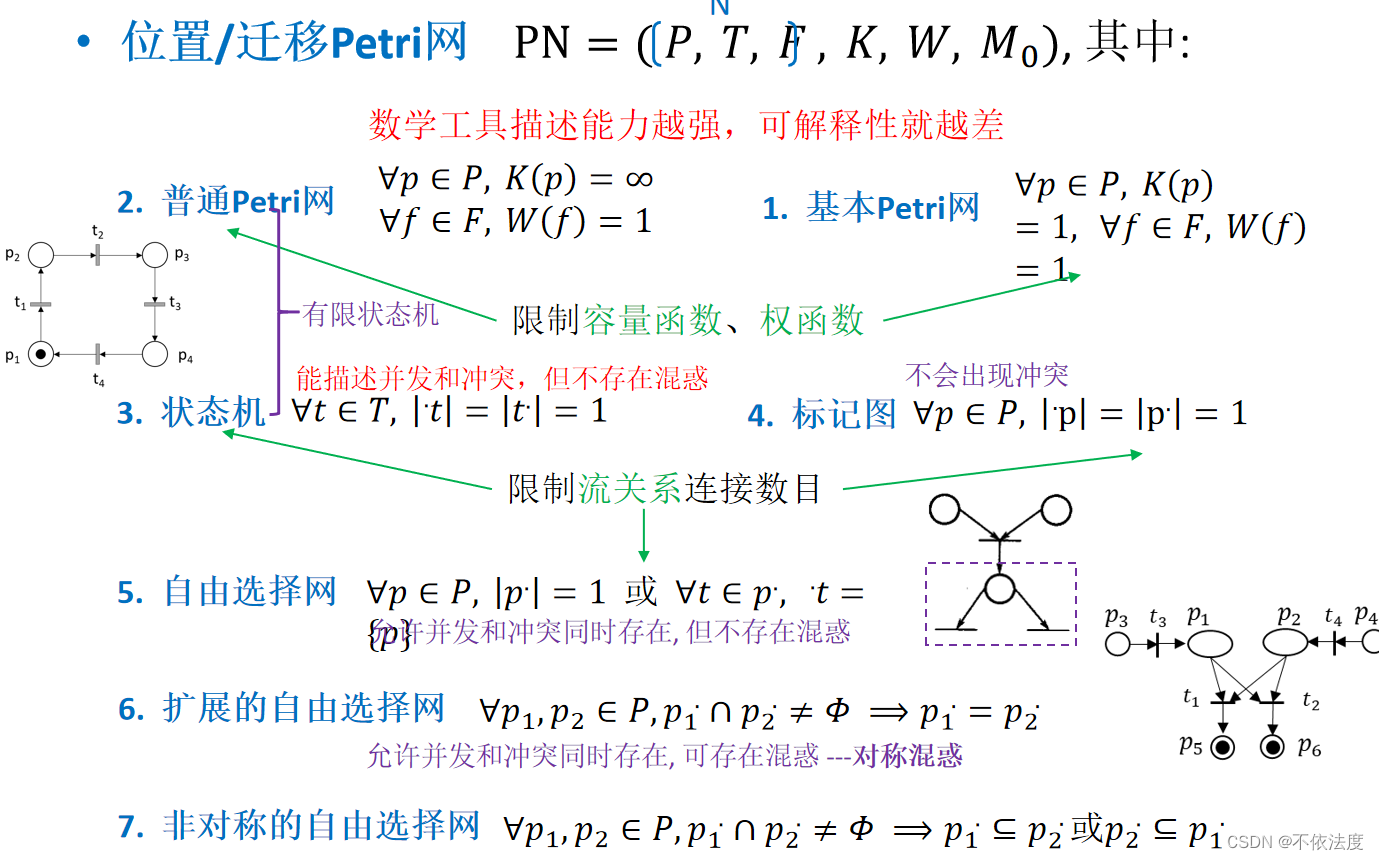
背不下来定义的话就记名字和举例的图还有性质就行。
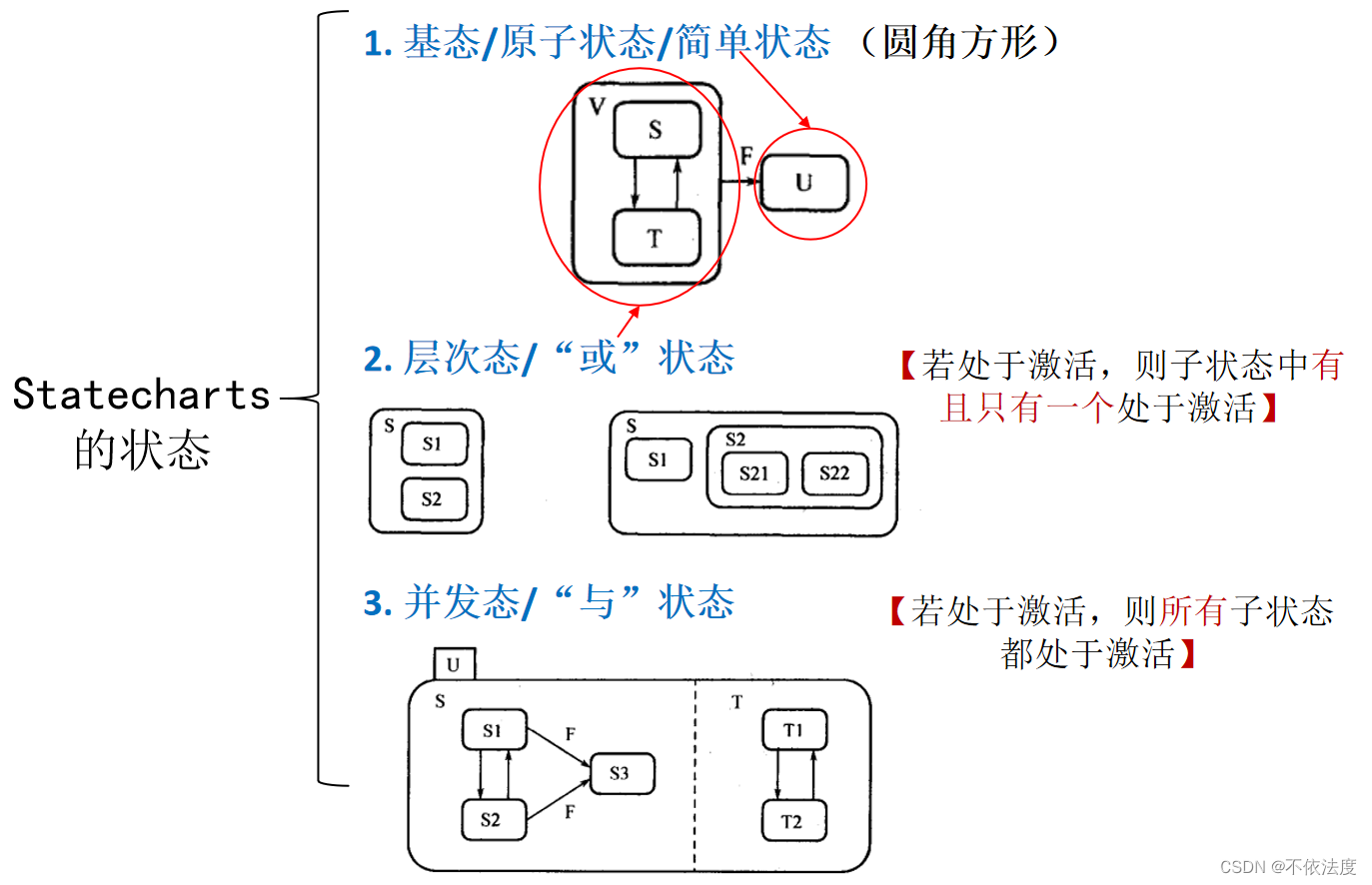
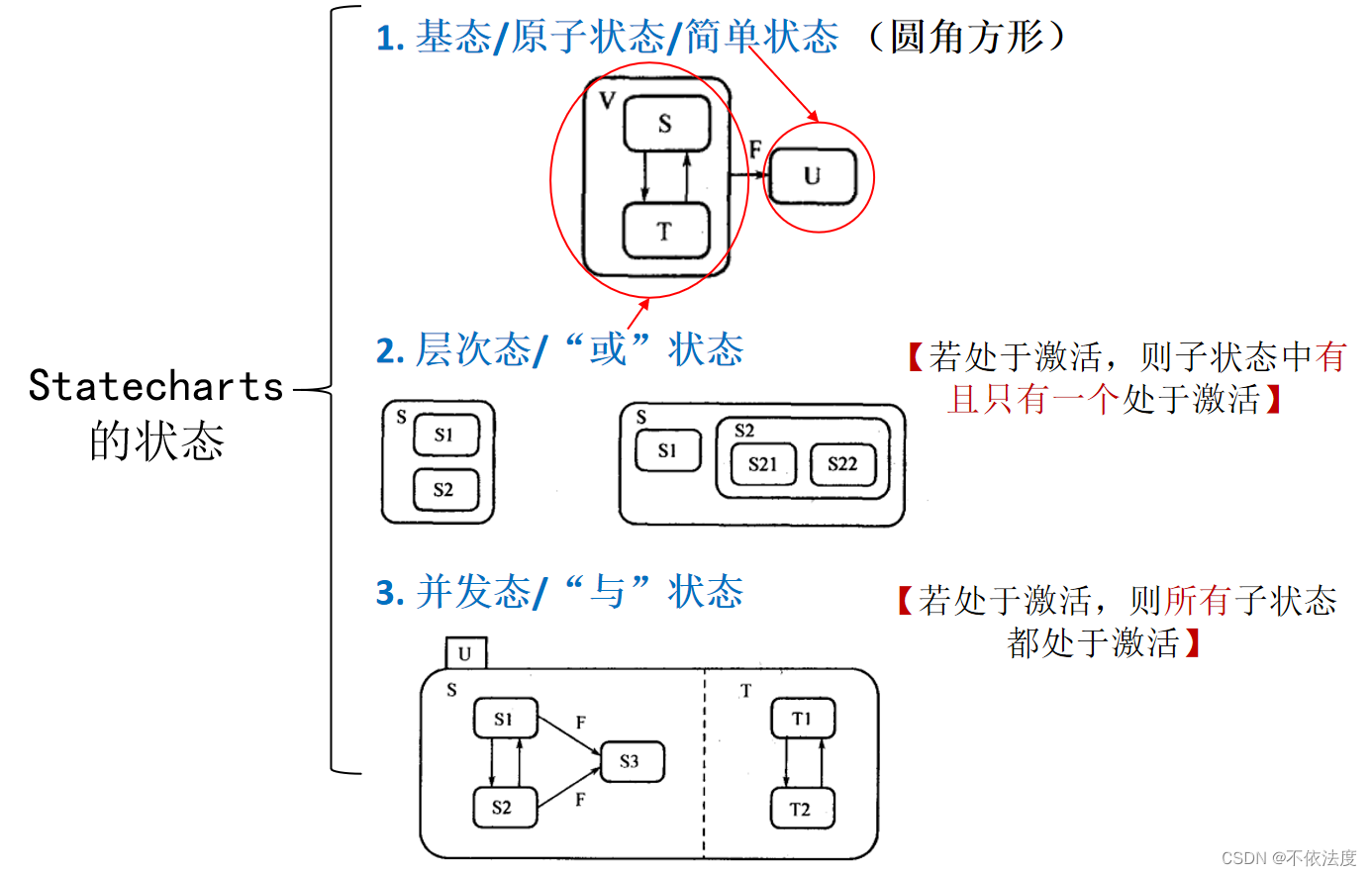
4.Statecharts 中状态节点的类型。
分析证明题
- 命题逻辑的演绎证明法:
(题目让用哪种方法就得用哪种方法,用其他方法会稍微扣点分)
a) 直接证明法
b) 间接证明法
c) 归结推理法(子句归结法) - 谓词逻辑:
a) 文字描述转谓词逻辑描述
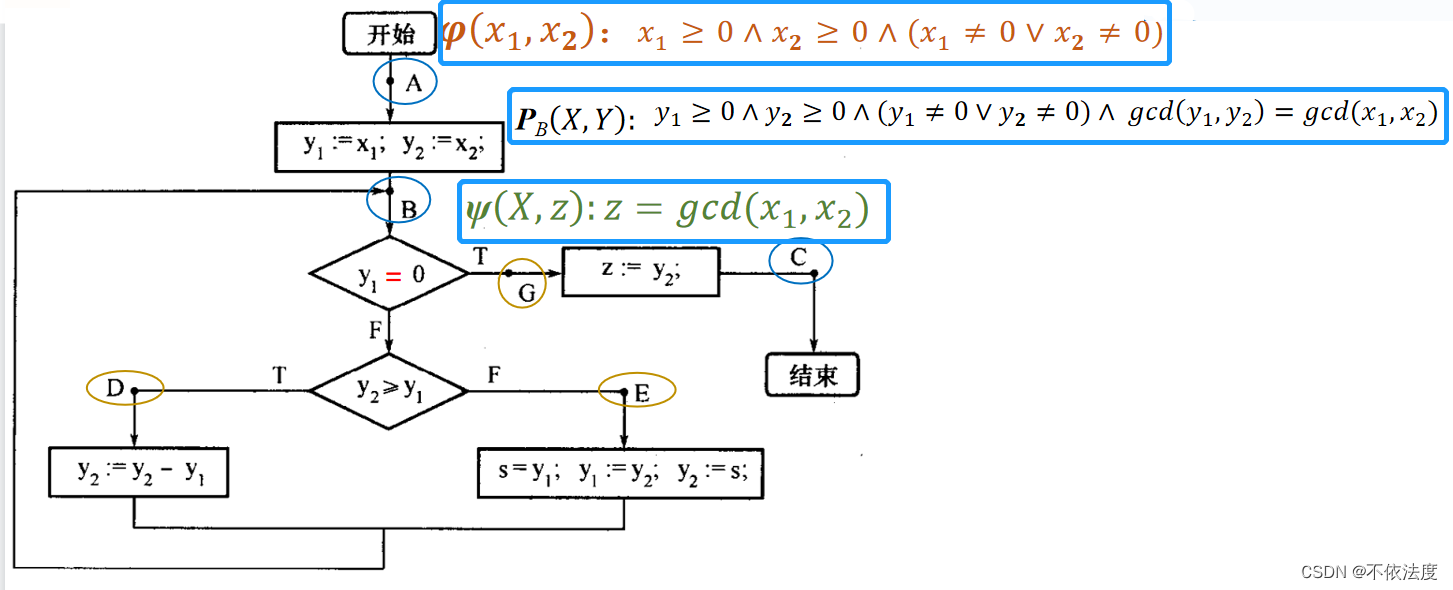
b) 谓词逻辑证明 - Floyd 前后断言法:例 5.3.1、例 5.3.2、课后 5.7
a) 归纳断言法 ---- 证明部分正确性
b) 良序集法 ---- 证明终止性 - Hoare 公理化方法,证明程序部分正确性 例 5.3.3、课后 5.8(1)
- Dijstra 最弱前置谓词法,证明程序完全正确性 P133 下数组求和题、课后 5.9
- 有限状态机:
a) 给出定义形式的一个有限状态机,画出其状态转移图、状态转移表、状 态转移矩阵;或给出状态转移图形式的有限状态机,写出其定义形式。
b) 写出有限状态机所接受的语言集合。 - Petri 网:
a) 化简。
b) 覆盖树生成。
c) 有界性、活性、可逆性分析。(可结合化简或覆盖树)
应用题
- 有限状态机 (课后 2.6、课后 2.8)、Moore 机 (图 2.4、课后 2.4(1))、Mealy 机 (图 2.5、课后 2.4(2)) 设计。
- Statecharts 设计电梯控制系统。
- Petri 网设计。 哲学家、例题生产线、课后生产线、生产者-消费者、消防
串行系统程序正确性证明
【关于离散数学的这两部分我写的有点多,其实会三种证明和文字转命题公式就行】
命题逻辑(关于离散数学的,很熟的可以略过)
记住一些定义
-
命题:陈述句 + 有确定的真值
-
真命题
-
假命题
-
命题常元:符号P表示一个确定命题时。
-
命题变元:符号P表示任意一个命题时。
-
原子命题:原子命题是不能再细分的命题。
-
复合命题:原子命题通过命题联结词构造的命题。
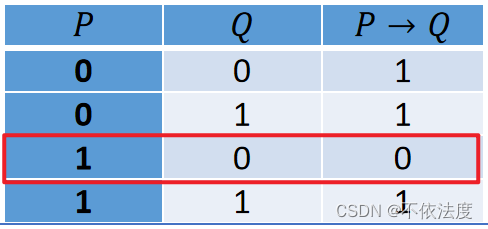
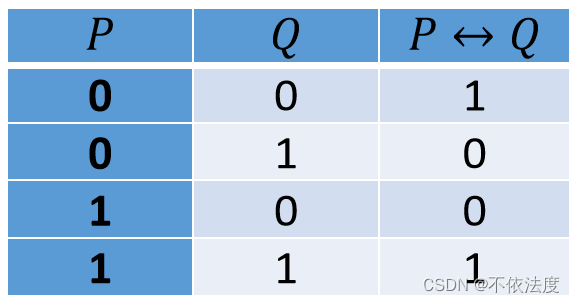
- 命题联结词:非¬ 合取∧ 析取∨ 蕴含→ 等价↔ ,计算就记个蕴含和等价就好。
记点命题文字转表达式的题目
- 他是这次离散数学考试的第一名或第二名。(P∧¬Q)∨(¬P∧Q)
- P:他步行上班,Q:天下雨。
2.1 除非天下雨,否则他步行上班。¬P→Q或¬Q→P
2.2 只要天不下雨,他就步行上班。¬Q→P
2.3 只有天不下雨,他才步行上班。P→¬Q
除非,否则这类连词,写的时候把除非后面的当条件,再加个非,否则后面的当结果就不容易写错:¬条件→结果
- 命题联结词:非¬ 合取∧ 析取∨ 蕴含→ 等价↔ ,计算就记个蕴含和等价就好。
-
-
命题计算的优先顺序:( )、¬、∧、∨、→、↔ 。
(∧与∨同一优先级从左向右顺序) -
命题公式:单个命题变元和命题常元是一个命题公式。有限次符合命题公式也是。
-
n元命题公式:含有n个命题变元P1、P2 ⋯、Pn,称G为n元命题公式,即G(P1、P2 ⋯、Pn)。
- 给P1、P2 ⋯、Pn分别指定相应的真值,称为对公式G的一种指派或解释。
- 使得G为1,则称这组值为G的成真指派。
- 使得G为0,则称这组值为G的成假指派。
-
真值表:列出所有0,1取值可能对应G的取值。
-
永真式:如果命题公式G在所有指派下真值为1,称公式G为永真式或重言式。
-
永假式:如果命题公式G在所有指派下真值为0,称公式G为永假式或矛盾式。
-
可满足式:如果命题公式G在有些指派下真值为1,有些指派下真值为0,称公式G为可满足式。
-
基本等价式,不考计算的话知道这个就行:蕴涵等值式:G→H =¬G∨H。
-
简单式
- 简单析取式:P∨¬Q
- 简单合取式:P∧¬Q
-
范式
- 析取范式:(析取式)∨(析取式)
- 合取范式:(合取式)∧(合取式)
-
【推导类题目用得到】记住这个符号 ‘ ⊢ ’ 的意思:设G1,G2,⋯,Gn是一组命题公式,H是命题公式,如果蕴涵式G1∧G2∧⋯∧Gn →H是重言式,称H是G1,G2,⋯,Gn的有效结论,G1,G2,⋯,Gn称为前提,可表示为 G1,G2,⋯,Gn ⊢ H。因为前提为假的时候整个蕴涵式恒为真,所以只需要判断前提为真时,结论是否恒为真。
-
推理常用的规则(写推导过程后面一列用到的)
- P规则(前提(题目给的)引用规则)
- T规则(推理引用规则)
-
推理方法【三个都要掌握,要会区分】
- 直接证明法
- 间接证明法:给定前提{G1,G2,⋯,Gn},则(G1,G2,⋯,Gn)→ S为重言式当且仅当 (G1,G2,⋯,Gn) ∧¬S)为矛盾式
- 【考了】归结推理法

谓词逻辑(关于离散数学的,很熟的可以略过)
还是一些定义
- 个体:
- 个体常元:表示特定的、具体的个体。通常用小写字母a、b、c等表示。也称为个体常项。
- 个体变元:表示泛指的、不确定的个体。通常用小写字母x、y、z等表示。也可称为个体变量、个体变项。
- 个体的取值范围称为个体域或论域。通常用D表示。
- 宇宙中所有对象的集合称为全总个体域,简称全域,它是默认的个体域。
- 性质
- 一元谓词P(x),表示个体的性质:x有性质P。
- n元谓词P(x1, x2, ⋯,xn),表示n个个体之间的关系,它是个体域为定义域,{0,1}为值域的n元函数或关系。
- 函数:描述个体域到个体域上的映射,通常以小写字母f, g, h…表示。f(x): x的父亲。
- 量词:表示个体常项、个体变元的数量关系的词称为量词,包括:全称量词∀和存在量词∃。
【考了,考的是给一段文字,转化成谓词逻辑公式然后证明】
看点例题还比较有用:
符号化下列命题。
- 凡人都呼吸。
令M(x)表示x是人;F(x)表示x呼吸;符号化为:∀x(M(x)→F(x))- 有的人用左手写字。
令M(x)表示x是人;G(x)表示x用左手写字;符号化为:∃x(M(x)∧G(x))- 不是所有的自然数都是偶数。
令N(x)表示x是自然数;E(x)表示x是偶数;符号化为:¬∀x(N(x)→E(x))或者∃x(N(x)∧¬E(x))
扩展一下
-
N:非负整数集合或自然数集合{0,1,2,3,…}
-
Z:整数集合{…,-1,0,1,…}
-
Q:有理数集合
-
R:实数集合(包括有理数和无理数)
-
公式G,如果在所有解释下,真值都为真,称G为有效公式或永真公式;如果在所有解释下,真值都为假,称G为矛盾公式或永假公式;如果至少存在一种解释使其为真,称G为可满足式。
-
前束范式:公式G中的一切量词都位于该公式的最前端(不含否定词),量词的辖域都延伸到公式的末端。如下:(Q1x1)(Q2x2)⋯(Qnxn)M(x1,x2,⋯,xn)
其中Qi为量词∀或∃(i=1,⋯,n),M中不再有量词。则称G为前束范式。例如:
∃y∀x∃z(A(x)→(B(x,y)∨C(x,y,z)))- 前束范式的求解步骤:
-
消去公式中的联结词“→”,“↔”(如果有的话)。有量词的德摩根定理中,‘非’要提到所属式子的量词前面。
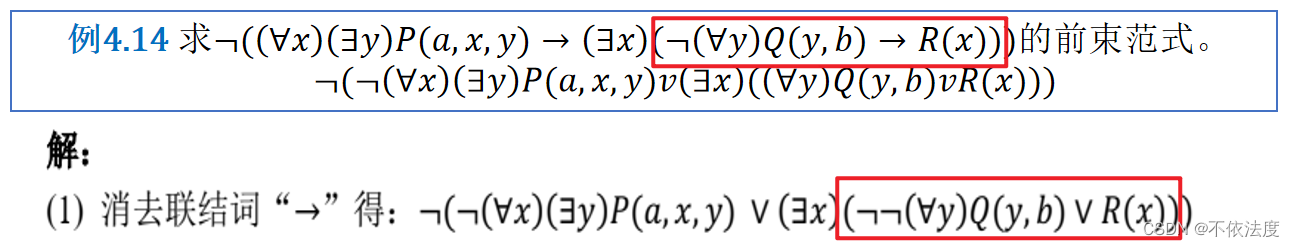
-
将所有的“¬”都内移到原子谓词公式的前端;(量词和谓词中间)
¬ ( ∃ x ) A ( x ) ⇔ ( ∀ x ) ¬ A ( x ) ; ¬ ( ∀ x ) A ( x ) ⇔ ( ∃ y ) ¬ A ( y ) ¬(∃x)A(x)⇔(∀x)¬A(x);¬(∀x)A(x)⇔(∃y)¬A(y) ¬(∃x)A(x)⇔(∀x)¬A(x);¬(∀x)A(x)⇔(∃y)¬A(y) (量词转换律)
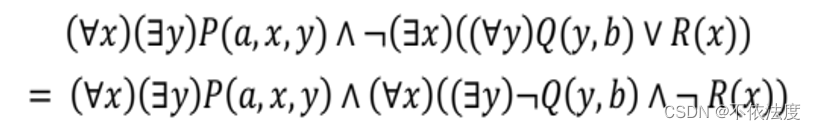
-
自由变元、约束变元在同一公式中仅以一种身份出现(管辖范围不一样的同名变元得换掉)
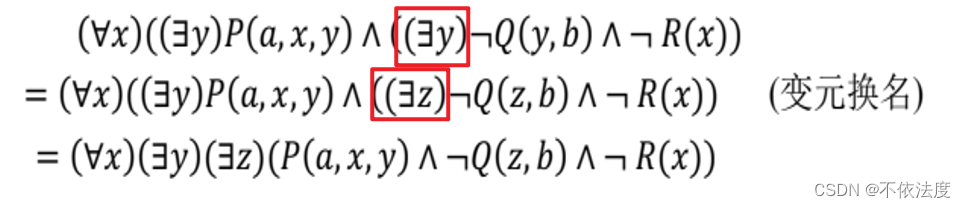
-
量词提到公式的最前端
-
辖域放到公式的末端。
-
- 量词分配律:(记不住,不记了,滚吧)
- (∀x)A(x)∧(∀x)B(x)= (∀x)(A(x)∧B(x))
- (∃x)A(x)∨(∃x)B(x)= (∃x)(A(x)∨B(x));
- (∀x)A(x)∨(∀x)B(x)= (∀x)(∀y)(A(x)∨B(y));
- (∃x)A(x)∧(∃x)B(x)= (∃x)(∃y)(A(x)∧B(y));
- 量词辖域的扩张律:
- (∀x)A(x)∨G= (∀x)(A(x)∨G);
- (∀x)A(x)∧G= (∀x)(A(x)∧G);
- (∃x)A(x)∨G= (∃x)(A(x)∨G);
- (∃x)A(x)∨G= (∃x)(A(x)∨G);
- 前束范式的求解步骤:
-
推理常用的规则(除了之前的P,T还有补充,写推导过程的时候要标注一下)
- P规则(前提引用规则)
- T规则(推理引用规则)
- 全称特指规则US: ∀xG(x) ⇒ G(c)
- 全称推广规则UG:G(c) ⇒ ∀x G(x)
- 存在特指规则ES:∃x G(x) ⇒ G(c)
- 存在推广规则EG:G(c)⇒∃xG(x)
证明程序正确性
(只整理了老师要求看的三题,太难的我就懒得去推了,考完发现足够了)

注意第三条就够了,φ(X)表示输入 , Q表示程序,ψ(X,Z)表示针对φ(X)输入产生的输出结果。
第三条的意思就是:对于每个使得φ(X)为真的X,既可使程序Q能终止执行,又可使得终止时ψ(X,Q(X))为真,则称程序Q关于φ是完全正确的。
将一个完整的程序Q拆成多个步骤Q1,Q2,…,Qn,证明每一个步骤的正确性,根据此出现以下几种证明方法。
Floyd前后断言法
- 建断言:设置断点,为每个断点处建立断言(断言可以理解为通路可走的约束)。
- 设通路检验条件:两个断点之间有一条通路,通路入口的断言看作该通路的输入断言(前断言),出口的断言为输出断言(后断言)。若通路部分正确,应有:
前断言⋀执行该通路的条件→后断言 - 所以需要证明每条通路的检验条件:前断言⋀执行该通路的条件→后断言
简短说就是在断点建立断言,并在断言的基础上证明每一条通路的正确性。
归纳断言法(证明部分正确性)
归纳断言法的解题思路
- 建断言:在程序开始处【φ(X)】、结束处【ψ(X,Z)】、及每个循环中【PB(X,Y),Y={y1, y2, …}是程序中引入的中间变量】各设置一个断点(一个循环多个分支每个分支都算一条通路,为了表示这些通路会添加一些辅助性的点),将断点以大写字母A、B、C…编号,并为每个断点处建立断言,且循环处断言应为循环不变式。【简单说,设断点 + 标号】
- 设通路检验条件:PI(X,Y) 表示通路的前断言,QIJ(X,Y) 是通路的执行条件,PJ(X,qIJ(X,Y))是通路的后断言,其中qIJ(X,Y)是执行通路后修改的变量(变量改变的操作)。
- 后续要证明检验的就是:PI(X,Y) ⋀ QIJ(X,Y) → PJ(X,qIJ(X,Y))
例题5.3.1
正整数应该改成非负整数
【例5.3.1考的是他的良序集法证明终止性,反正也不难,可以现推】
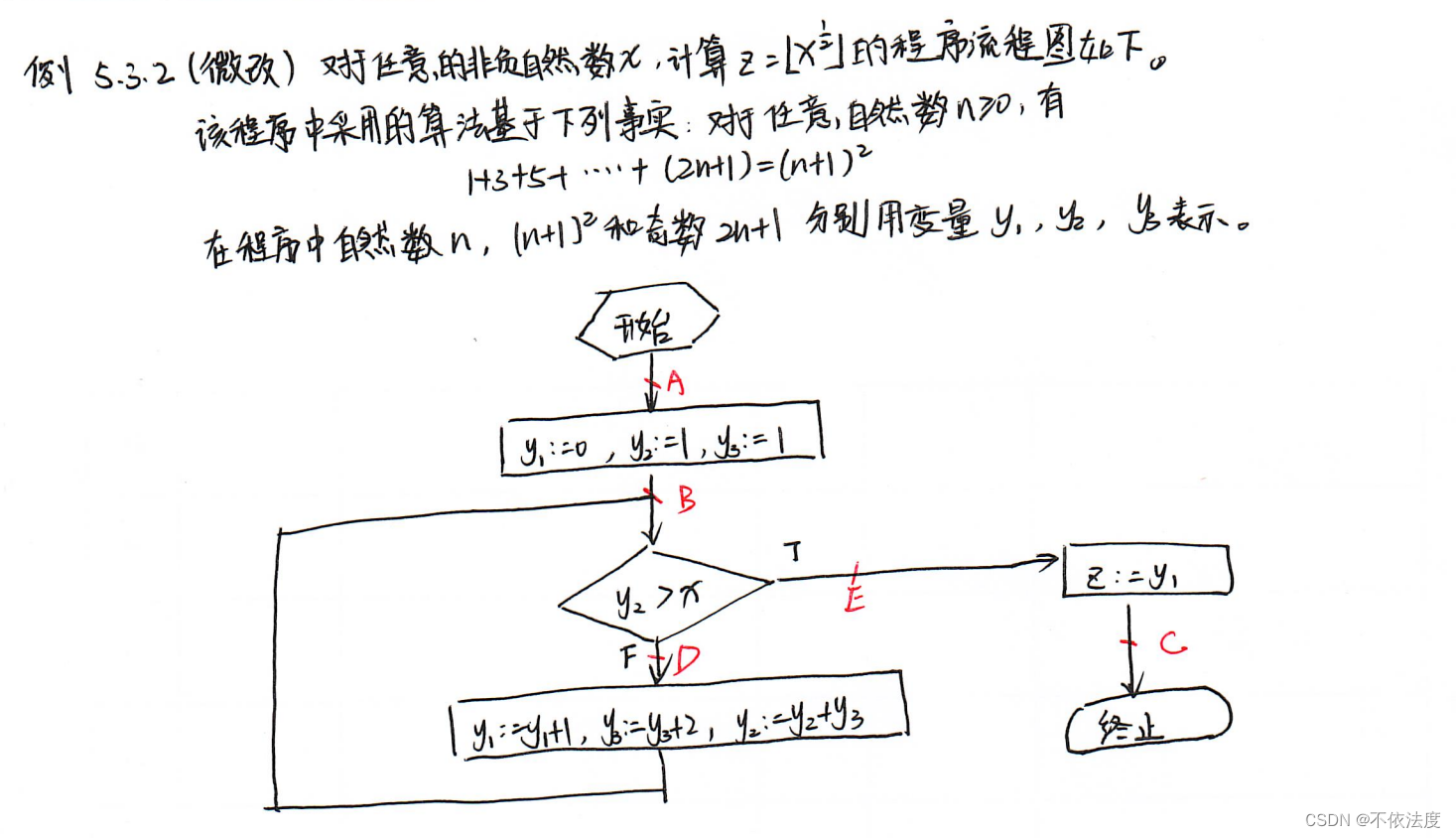
例题5.3.2
良序集法(证明终止性)
【考了,考的例5.3.1】
先了解一下偏序及偏序集
- 设≺为非空集合A上的关系,如果≺满足自反性、反对称性以及传递性,那么≺是集合A上的偏序关系,集合A与关系≺一起称为偏序集,记作<A, ≺>
- 自反性: ∀a∈A都有a≺a ,称≺满足自反性。比如≤关系:1 ≤ 1。
- 反对称性: ∀a, b∈A,如果a≺b且b≺a,则a=b。称≺满足反对称性。同样≤关系:如果a ≤ b且b ≤ a,则a = b。(反对称不是不满足对称的意思)
- 传递性: ∀a, b, c∈ A ,如果a≺b,b≺c,则a≺c,称≺ 满足传递性。同样≤。
关于良序集:
- 设<A, ≺>为偏序集【偏序集是前提】,若A中每个非空子集关于≺均存在最先元素,则称<A, ≺>为良序集。实数的≤关系就不是,但是自然数[0,1,2…]的≤关系是的。
Floyd良序集法的解题思路
- 建断言:为程序开始处【φ(X)】及每个循环【FI(X,Y) 】中设置断点 (结束处不需要设置了) ,并为每个断点处建立断言,且循环处断言应为循环不变式。
- 选取良序集:<W,≺>, 在每个循环断点处定义一个良函数fI(X,Y) 。 ( 最常用的良序集是<N, < >
【其实<是存在问题的,< 不满足自反,但是各教科书都是<,老师也不知道什么情况,所以不管了,先这么写吧】。 - 证断言是良断言:QIJ(X,Y)表示通路I - J的执行条件,FI(X,Y)是断言, qIJ(X,Y) 表示经通路修改的中间变量(变量变化)。则通路I-J可达条件如下:
F I ( X , Y ) ⋀ Q I J ( X , Y ) → F J ( X , q I J ( X , Y ) ) F_I(X,Y) ⋀ Q_{IJ}(X,Y) → F_J(X,q_{IJ}(X,Y)) FI(X,Y)⋀QIJ(X,Y)→FJ(X,qIJ(X,Y)) - 证所定义函数为良函数:即对于每个循环处断点都有 F I ( X , Y ) → f I ( X , Y ) ∈ W F_I(X,Y)→ f_I(X,Y)∈W FI(X,Y)→fI(X,Y)∈W。这个式子的意思是:如果循环处的断点可以执行F,变量代入f函数一定是属于良序集W的。这里的断言F和前面的断言P作用不一样的,断言F是为了让函数在良序集W内且有下界,断言P的为了证明正确性。
- 证每条通路上终止条件成立。
F I ( X , Y ) ⋀ Q I J ( X , Y ) → f I ( X , q I J ( X , Y ) ) ≺ f I ( X , Y ) F_I(X,Y) ⋀ Q_{IJ}(X,Y) → f_I(X,q_{IJ}(X,Y)) ≺f_I(X,Y) FI(X,Y)⋀QIJ(X,Y)→fI(X,qIJ(X,Y))≺fI(X,Y): fI(X,qIJ(X,Y)) 中的qIJ(X,Y)是执行完通路后改变的变量,fI(X,Y)中的Y是改变之前的变量。意思就是改变后的变量量在f关系上先于改变前的的变量。所以随着循环的执行,Y的变量取值逐渐逼近良序集的下界,就是可终止的。

例题5.3.2
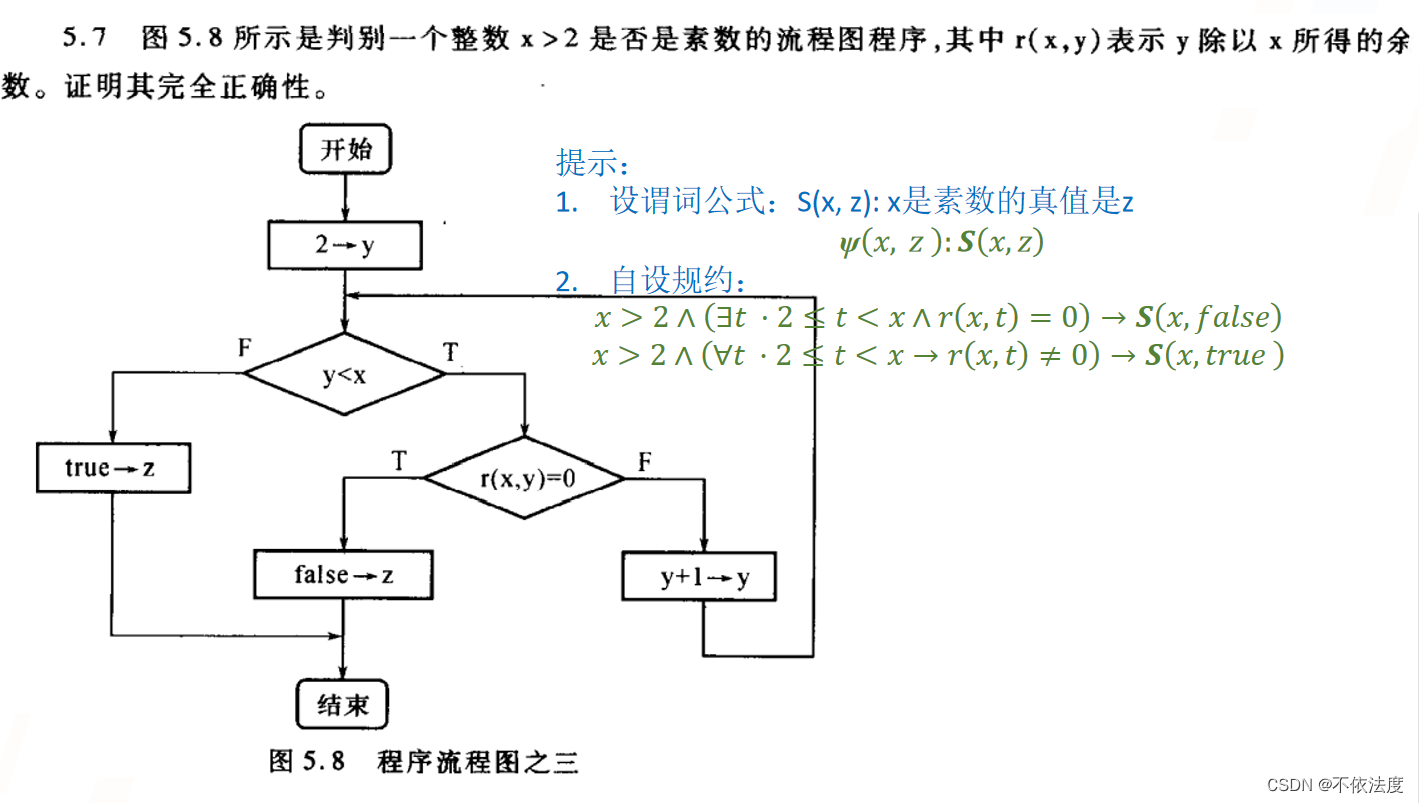
课后5.7
关于前后断言法的一些个人理解
- 归纳法中对于循环处设的断言的目的在于判断该断点延展的各条通路是否都能走通,所以这里的断言主要目的是满足所有通路的行走条件。
- 比如课后5.7的PB:y≥2 ∧ (∀t ⋅2≤t<y→r(x,t)≠0),能走到此刻的断点说明2 ~ y-1已经判断过不是x的质数,y≥2 ∧ (∀t ⋅2≤t<y→r(x,t)≠0)自然成立。
- 比如例5.3.2的PB:y12≤x ∧ y2=(y1+1)2 ∧ y3=2y1+1。因为z=y1= x 1 2 x^\frac{1}{2} x21,无论走哪一条通,y12≤x恒成立。
- 良序集法中对于循环处设的良断言的目的在于保证良函数的取值始终在良序集内。
- 比如课后5.7的良函数fB(X,Y)=x-y,为了保证x-y≥0(x,y皆为整数),所以FB(X,Y):y≥2 ∧ x≥y。
- 比如例5.3.2的良函数为fB=x-y2+y3,那么良断言就是x≥y2-y3 ∧ y3>0。这题其实良函数也可以设为x-y2,良断言用x≥y2 ∧ y3>0就行(当然我没试过后面这种写法是否能推断处终止,不过老师给了这种解法)。
上面几个例题是满足这个理解的,其他的就不知道了,没推理过。
- 关于良函数一般根据循环的判断条件就可以得出,你只要保证得出的良函数随着变良的改变逐渐逼近良序集的下界就行。
Hoare公理化方法(证明部分正确性)
{P}Q{R}:如果在程序Q执行之前有P成立,并且Q能终止执行,则在Q终止执行后必有R成立,通常将P,R成为前置断言,后置断言。
也是证明部分正确性,这里的断言喝归纳断言法的断言的作用是一样的。差别在于归纳断言是针对流程图,而Hoare公理化方法是针对程序。

公理化方法的做题思路
- 对初始处和结束处设断点。
- 将程序划分成更小的程序,对小程序的边界处设置断言。
- 简单写一下φ{Q}ψ分化成哪些Pi{Qk}Pj。
- 每一个Pi{Qk}Pj对应一个Goal,根据推理规则和公理将Coal转化成Log [ + Goal]。
- 比如一个关于循环的Goal(简单循环,循环内部没有什么条件顺序语句了), Pi{Q}Pj转换成Goal1:Pi ∧ B {Q2B} Pi 和 Log:Pi ∧ ¬B → Pj(这个是根据推断规则推理Goal1出来的,B是循环的判断条件,Q2B是循环体内部的语句)。要证明Goa1:Pi{Q}Pj就转换成证明Goal2:Pi ∧ B {Q2B} Pi 和 Log1:Pi ∧ ¬B → Pj了。证明Goal2:Pi ∧ B {Q2B} Pi 又要转化成Log2:Pi ∧ B → Pi,反正就是一直推理Goal,直到Goal全变成Log和可以用公理无需证明的Goal(这种Goal就可以省略了)
- 如果Goal1推理出的Goal2可以用赋值公理,那么这个Goal2就不需要再推理了,Goal2可以直接省略。比如Goal1:Pi{赋值语句}Pj,推理出Log1:Pi → Pj(X,g(X,Y))和Goal2:Pj(X,g(X,Y)){Y=g(X,Y)}Pj(X,Y)【注意看P的下标】(Goal2可以利用赋值公理,无需证明,这种就可以省略不写,变成要证明Goal1转换成证明Log1)。
- 证明每一个Log 。
例5.3.3
这题真的写死我了,好多。
课后作业5.8(第4步和第5步我这次合起来写了)
Dijkstra最弱前置法(证明完全正确性)
【考了,考的斐波那契数列,不过函数和断言老师都给设好了】
相当于是给了定理教你怎么设置断言。
最弱前置谓词 / 最弱前置条件wp
wp(Q, ψ): 使程序Q执行能够终止,且终止后ψ成立的最弱的那个谓词公式。
wp(Q, ψ): ∀P(X),满足P(X)→Q终止∧ψ(X),都有P(X)→wp(Q, ψ)
最弱前置法
- 基本思想:
找到wp(Q, ψ), 若φ(X)→ wp(Q, ψ), 则φ(X)→Q终止∧ψ(X, Z) 。 - 目的:
找到wp(Q, ψ)
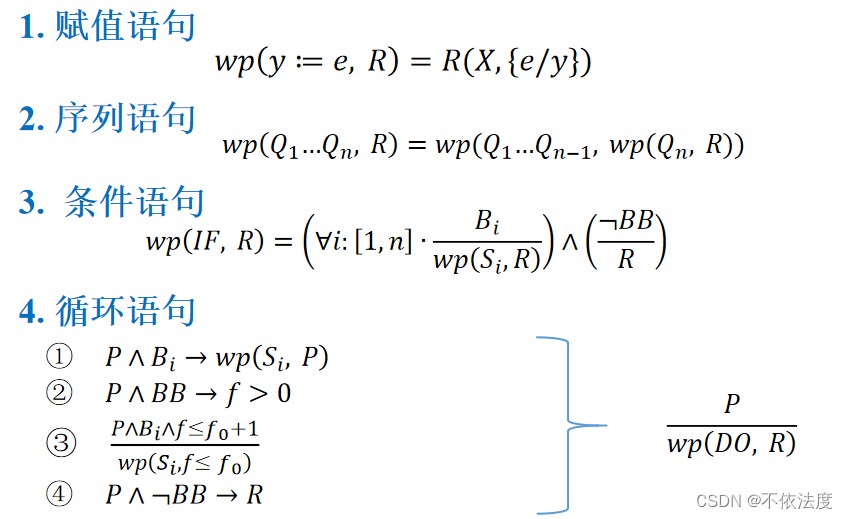
- 赋值语句:如果是赋值操作,把赋值结果带入赋值后的执行语句R就是wp。
- 条件语句:Bi是if语句的每一个条件,Si是Bi条件对应的执行语句。
- 循环语句:用了泛化的方式,不求最弱,只求是前置条件。BB是循环满足的条件,¬BB是循环语句不满足的条件。f 就类似良函数,这里叫作整型函数(求良函数一般就是看循环条件)。
(如果循环内部有if语句,if语句首先满足循环的判断条件BB,然后每一条if的判断条件Bi是对循环判断条件的拆分)循环语句的Bi是循环内部if语句对应的条件,Si是Bi条件对应的执行语句。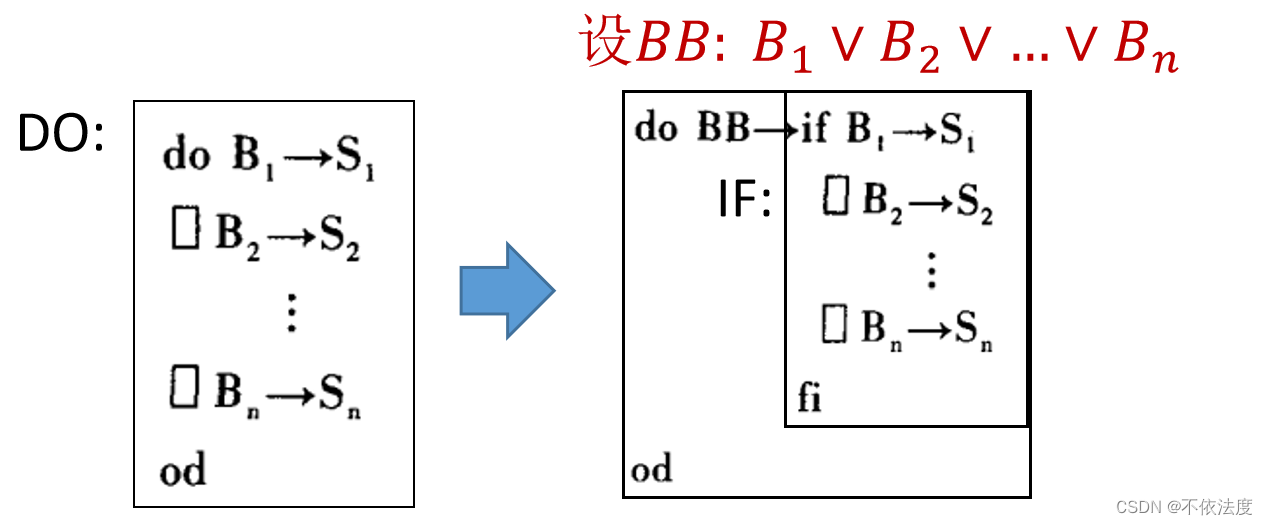
只要P满足四个条件,就能推出P→wp(DO, R),P是前置条件。
两个关于良函数的两个IF条件的,把(4)放到(1)后面比较好记。
最弱前置法的解题步骤
-
证明φ → ψ。
-
根据上面的语句分解φ → ψ,分步证明。
- 如果出现循环
- 根据上面的语句推导出谓词P(理解成断言就行)及整型函数f(理解成良函数)【这一步就是一个推导过程,卷面上可以不写】。
- 证明P是否满足对应的条件,比如如果P是循环的断言,那么就要满足循环的四个条件。
- 如果出现循环
-
综上,该程序具有完全正确性。
课本P133页数组求和
这题就是根据循环语句求出P(循环的前置条件),得到P→R(ψ),要证φ → ψ还需证明φ → P,两个都得证即退出φ → ψ。
课后5.9
恭喜我最讨厌的推理证明部分结束了!
并发系统建模模型
有限状态机
基本概念
状态转移函数,状态转移矩阵/关系矩阵,状态转移表,状态转移图
关系矩阵和状态转移矩阵写法一致,含义略有不同:
- 状态转移矩阵有动态的含义,比如Aij = x表示接收x后从i状态跳转到j状态。
- 关系矩阵类似词典,它的存在是便于查找两个元素之间的关系。

定义形式
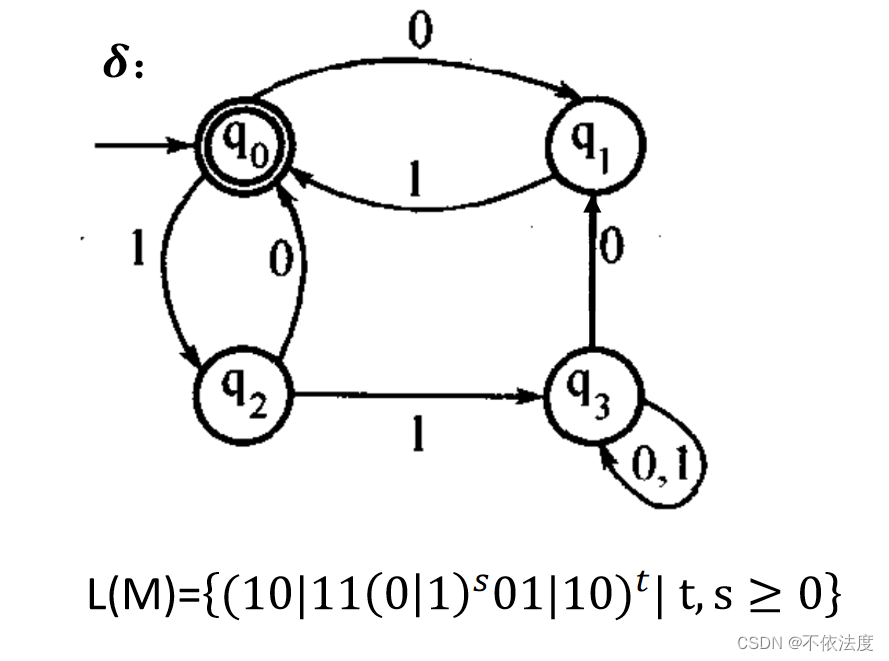
【考了,不是原题】
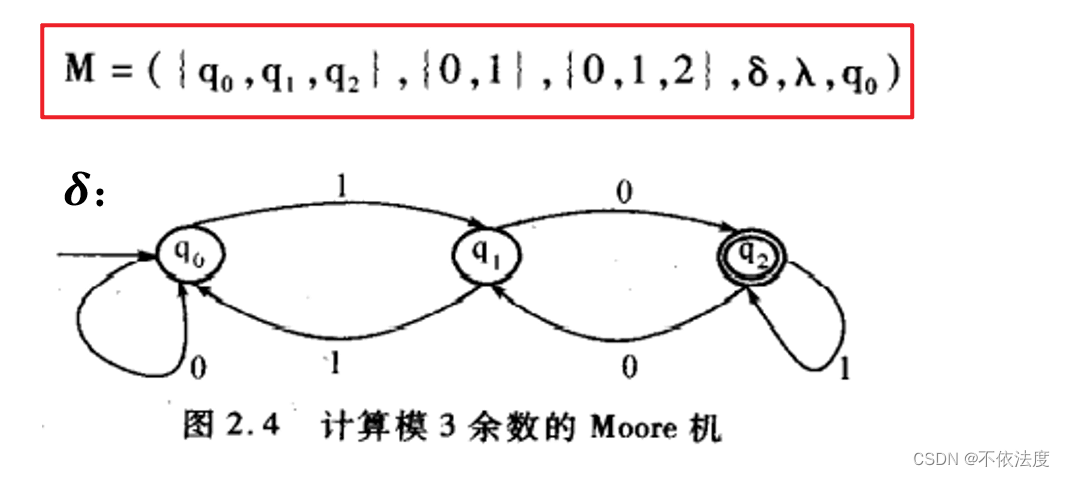
所接受的语言集合
【考了,不是原题】
最左边的箭头指向开始状态,双环表示结束状态。
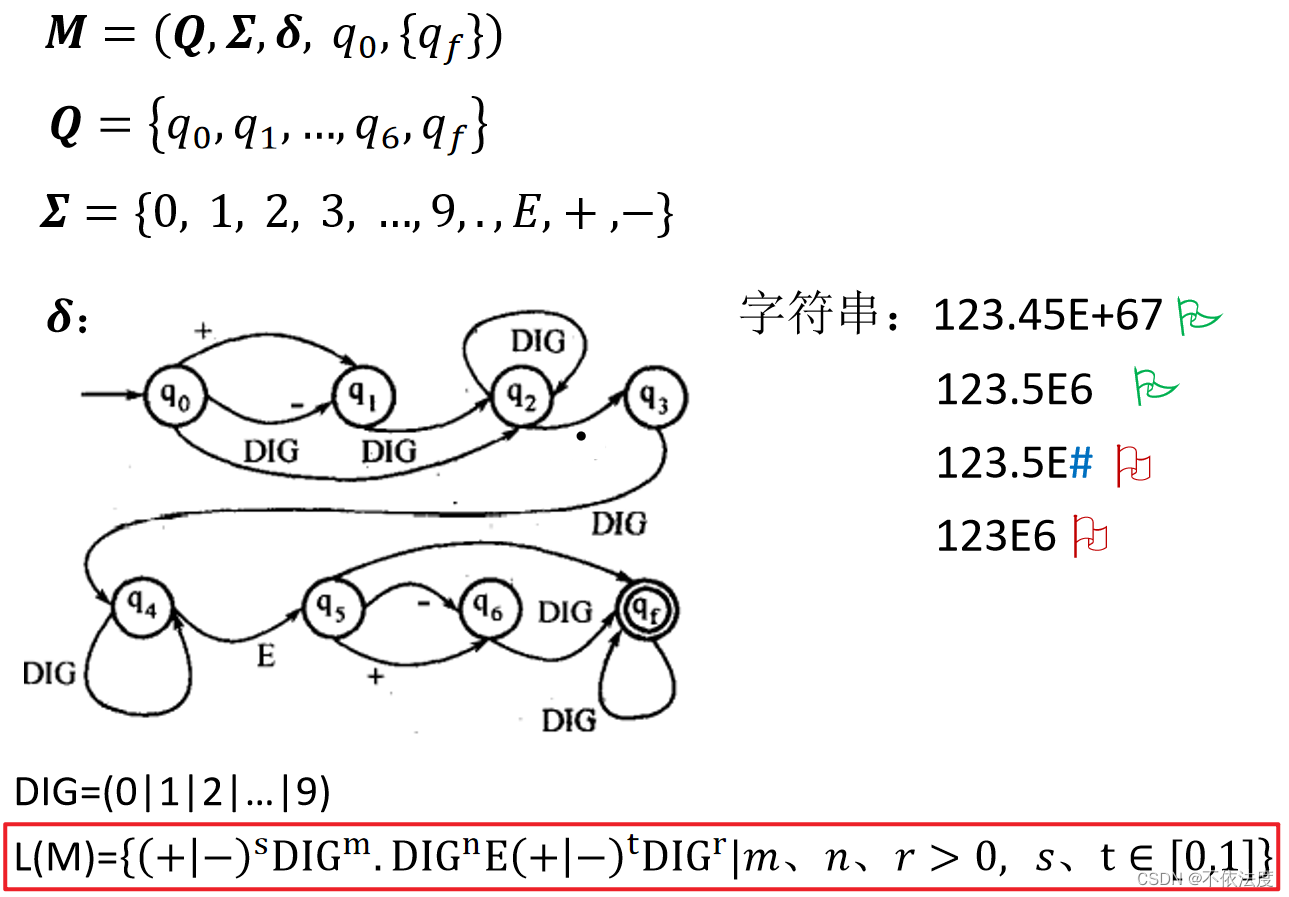
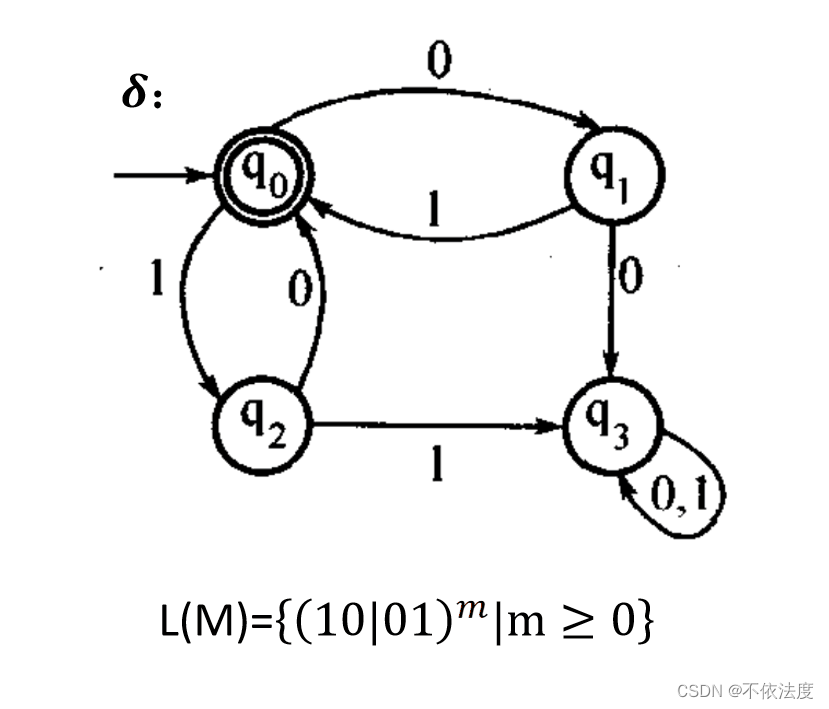
多弄了几道例题来看看。
例题1
例题2
例题3、4
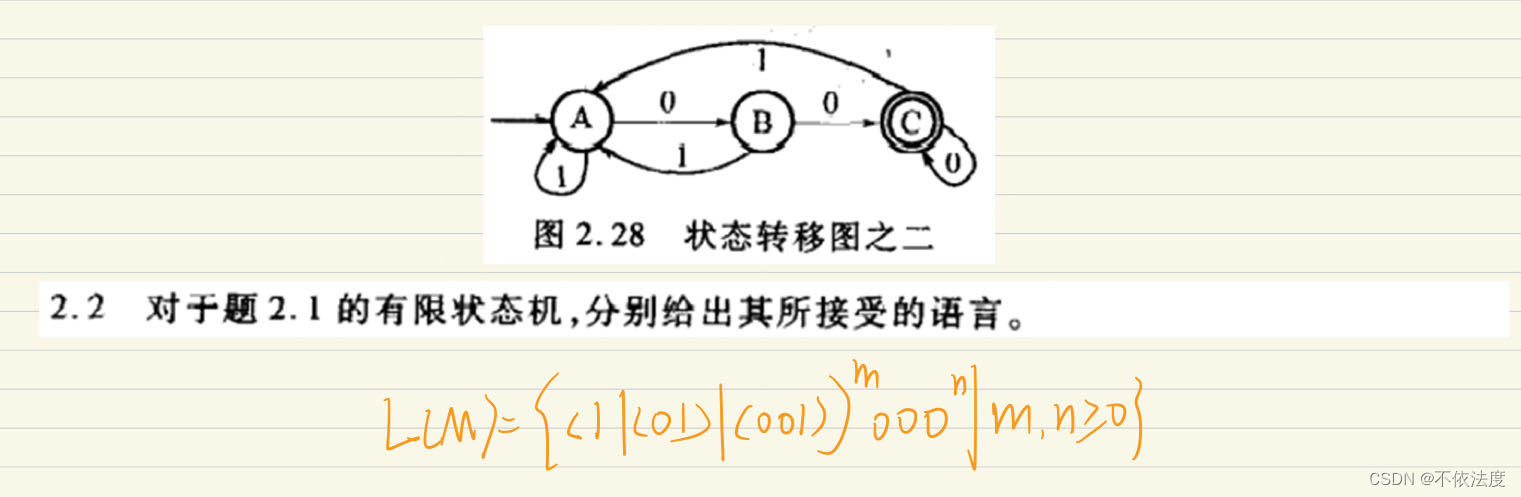
当m为0的时候空串{ε}也包含了(老师原始的ppt有点问题,和老师核实确认过改了一下)
这个和上面的不太一样(q1到q3的箭头变了)
有限状态机不能输出,只能通过能不能达到终态来判断字符串合不合法。
- 有限状态机的定义

- 确定状态机接收一个输入字符下一刻只有一个确定转移的状态,而非确定接收一个输入字符下一刻可能会有多个转移的状态。
- 语言:给定字母表Σ上的字符串的集合称为语言,以L表示。语言就是一串满足状态机从初始状态走向终态的字符串序列(感觉这样解释更好,还是不懂的得去翻编译原理的书)。
- 字符串:由字符组成的有限序列。
- 不包含任何字符串的语言称作空语言, 用ϕ表示, {ε}不同于ϕ。
- Σ∗:Σ上所有字符串连同空串ε一起构成的语言用Σ∗表示, 显然任意L⊆Σ∗。
- L(M):对于输入串x⊆Σ∗, 有δ(q0,x)=q′∈F, 则称字符串x被有限状态机M所接受, 或者称x为有限状态机M所接受的句子 (合法字符串)。被M接受的全部字符串构成的集合, 称为有限状态机M所接受的语言, 记作L(M)={x|δ(q0,x)∈F}
有限状态机的笛卡尔积复合
有限状态机的笛卡尔积复合定义了多个有限状态机的相互独立运行。
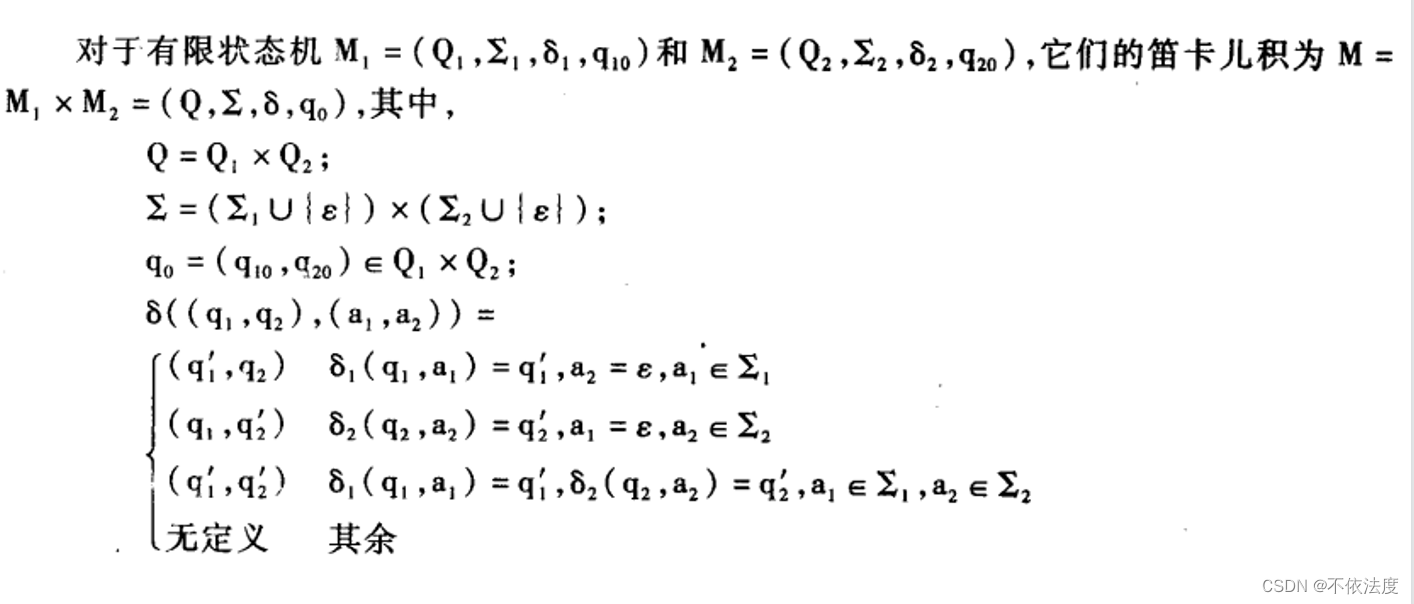
有限状态机的同步积复合

有限状态机的异步积复合

区分一下三种复合:
- 笛卡尔积 ×:各按各的输入字符走。
- 同步积复合 ⓧ:只有一种输入符,拥有该输入符的状态都可以走。(资源是无限的,只要有需要都可以拿资源)
- 异步积复合 ⊕:只有一种输入符,拥有该输入符的状态只有一个可以走。(资源是有限的,一次最多只有一个状态可以拿资源)
课后2.6
课后2.8
B1和S1应该是双环
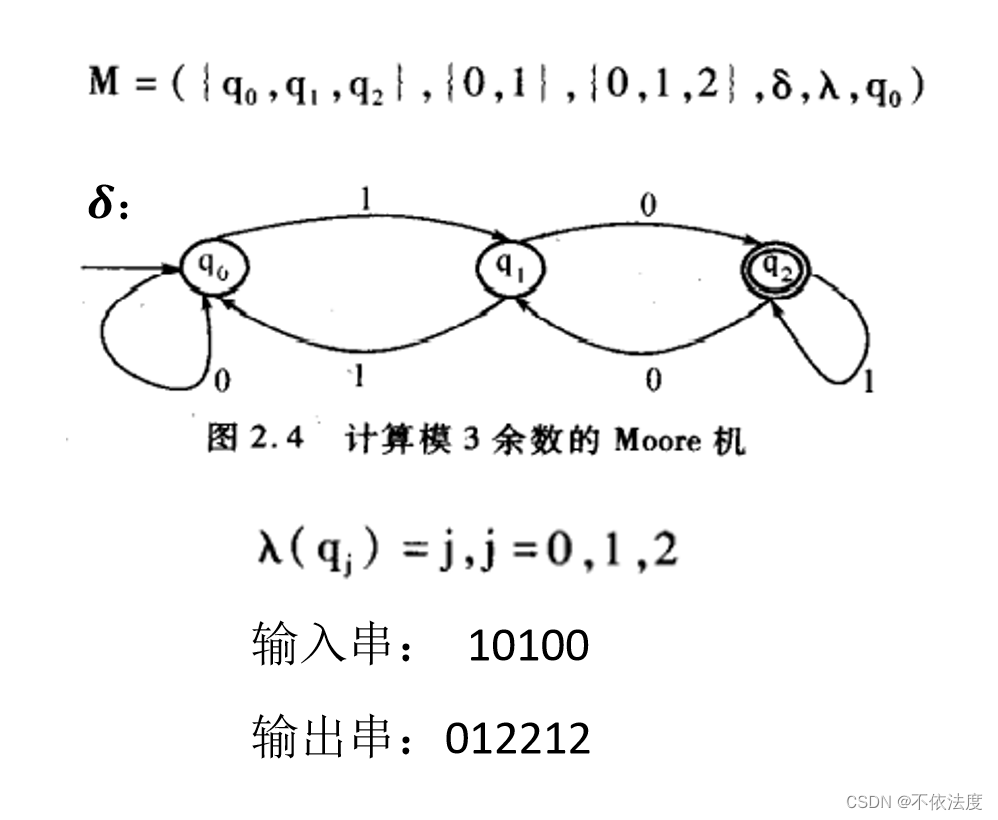
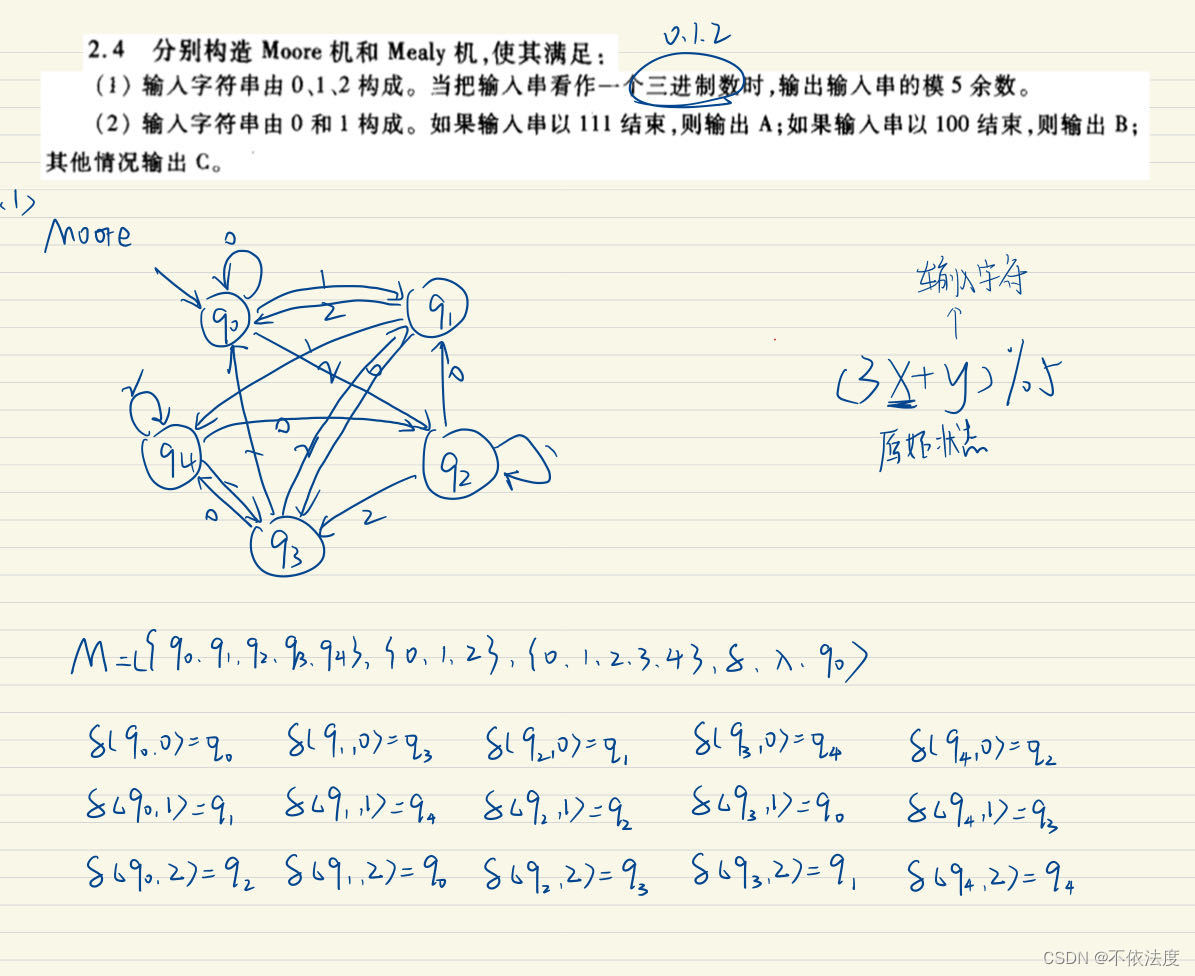
Moore机(输出与状态有关)
和有限状态机的区别:多了一个输出字符集合和输出函数,然后终止状态集合F去掉了。

图2.4
这题输出函数是和状态关联的,所有一到一个状态就有输出,所以初始未输入任何字符时处于q0输出0。
课后2.4(1)
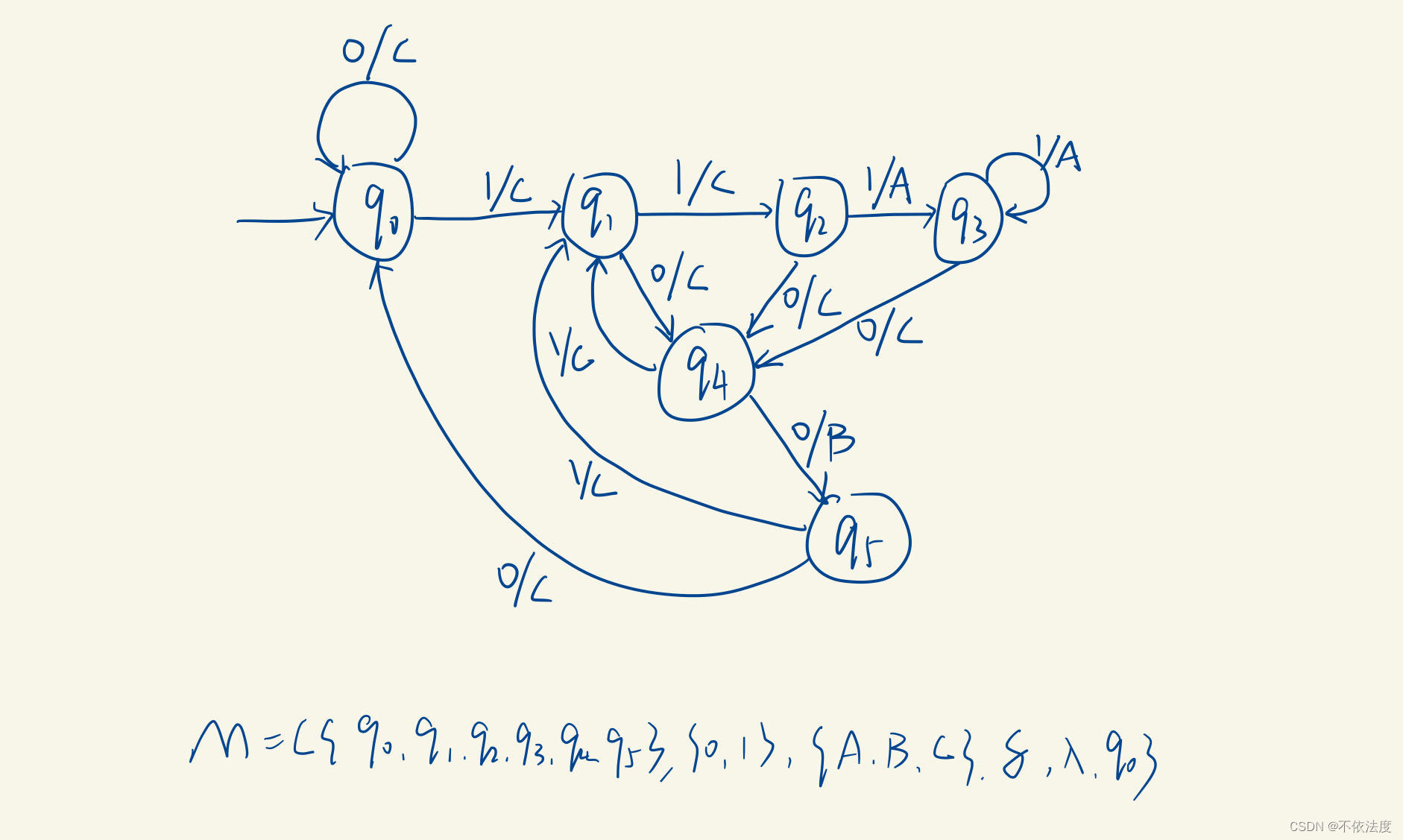
【考了,原题】
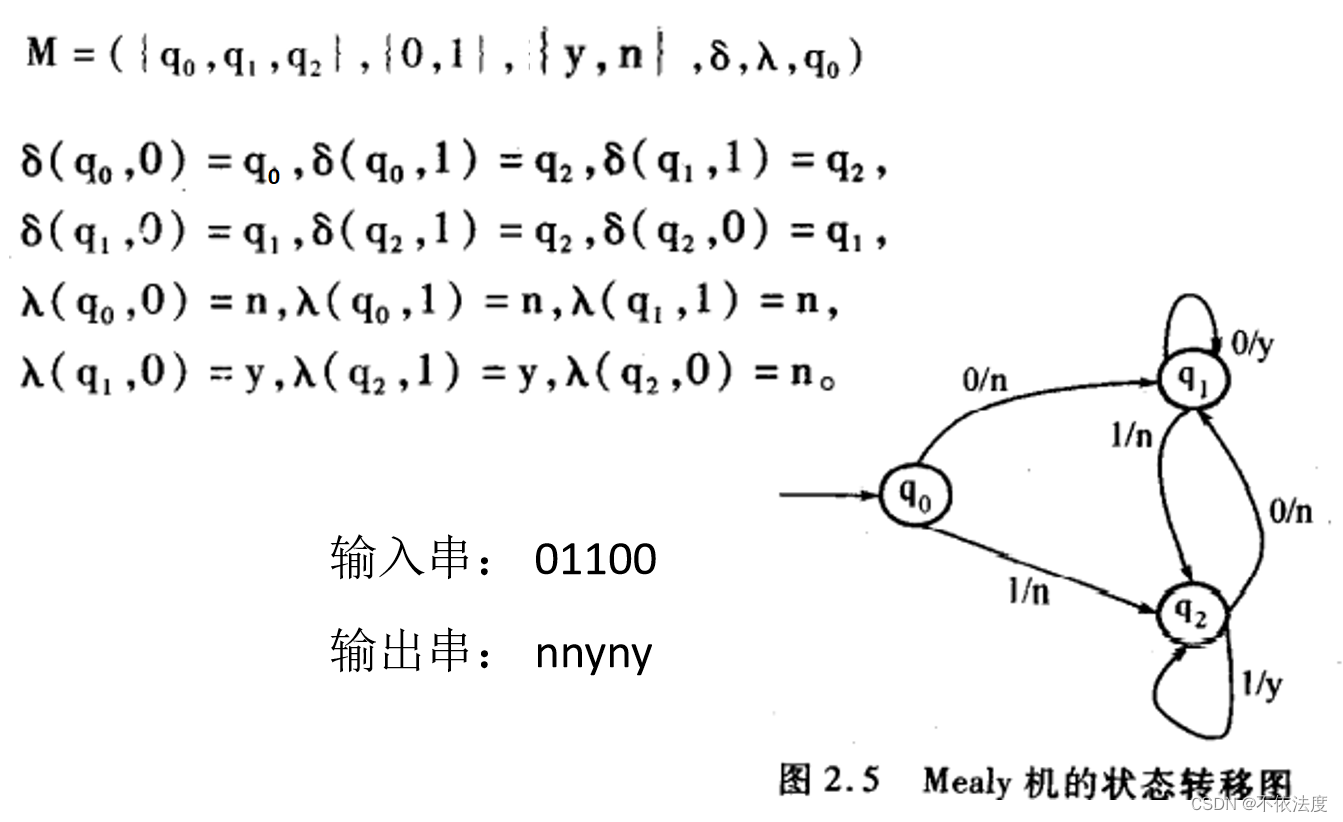
Mealy机(输出与输入有关)
和Moore机差不多,就是输出函数那边从Q → ▲变成Q × Σ → ▲。

图2.5
状态转移线段上标的是【输入/输出】
课后2.4(2)
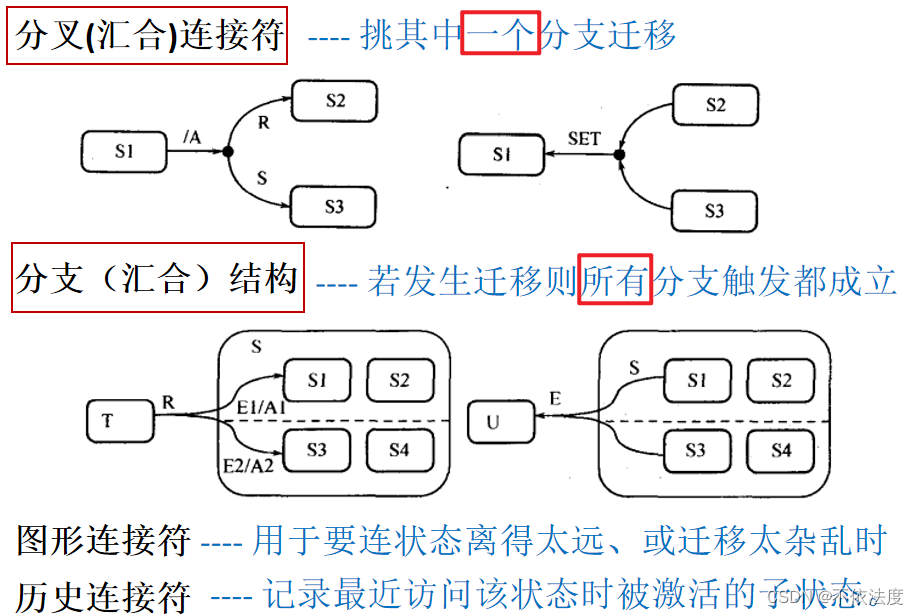
Statecharts
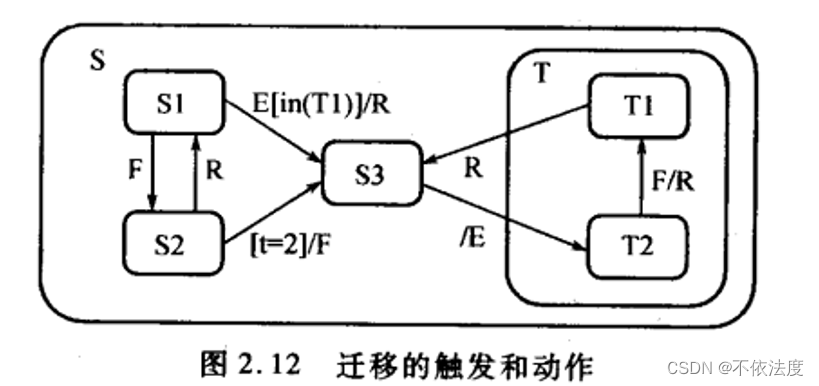
迁移的表示:触发/动作
- 触发:事件[条件]/事件、读写数据、
- 动作:修改条件活动状态
迁移:触发/动作
- E:动作可以缺省,如果只有触发,‘/’可以省略。
- E[…]/R:触发/动作。
- /R:只有动作,‘/’不可以省略。
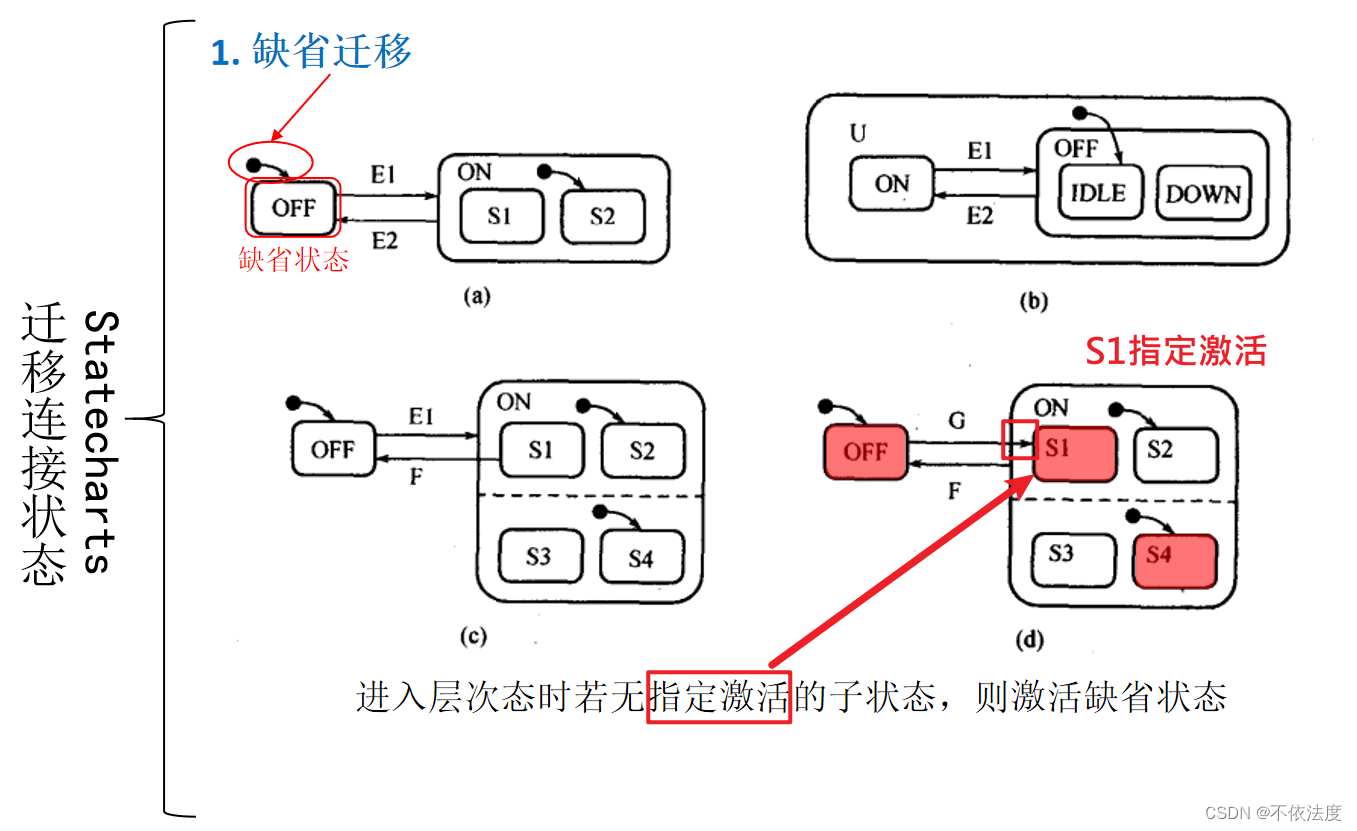
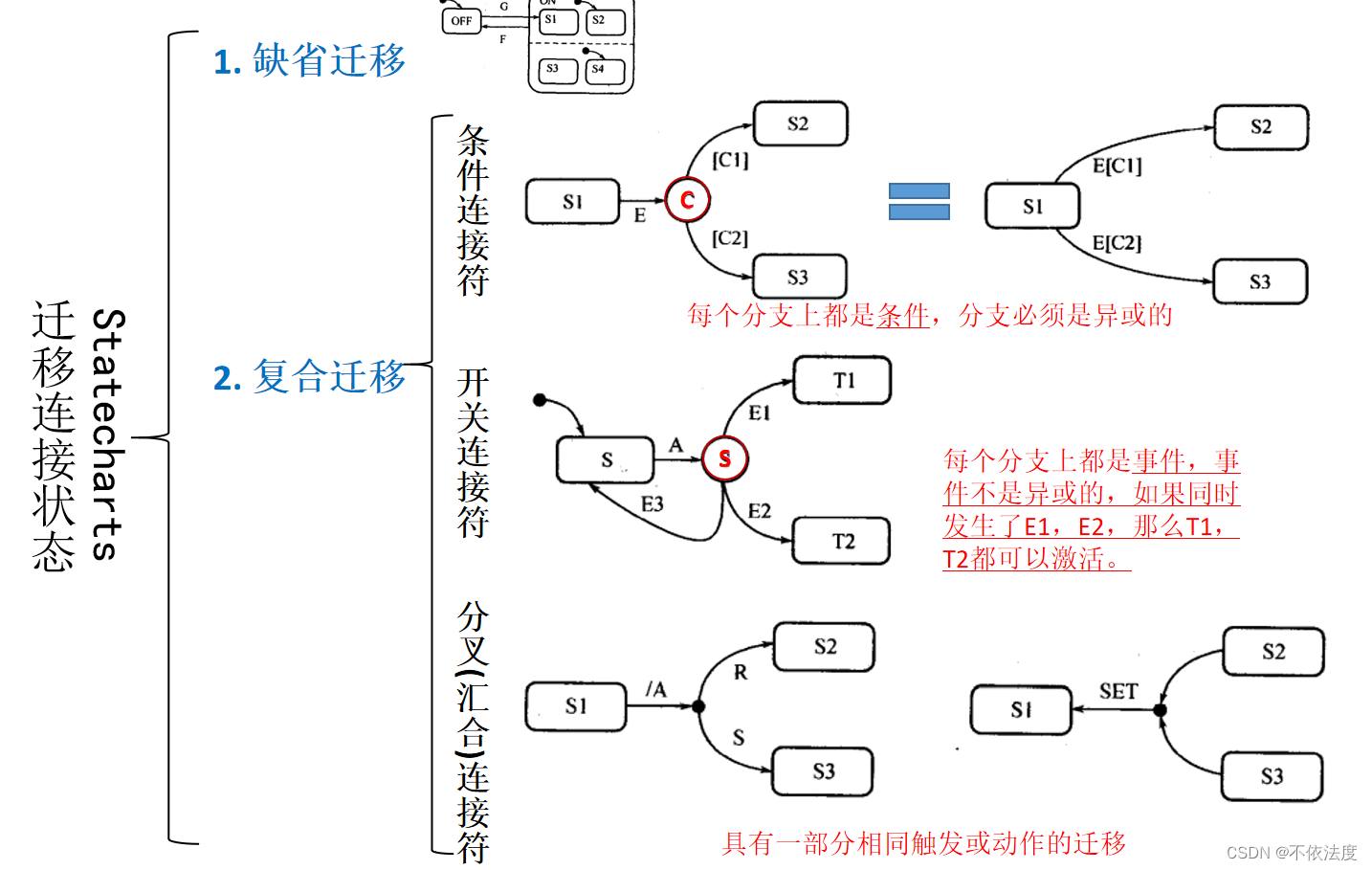
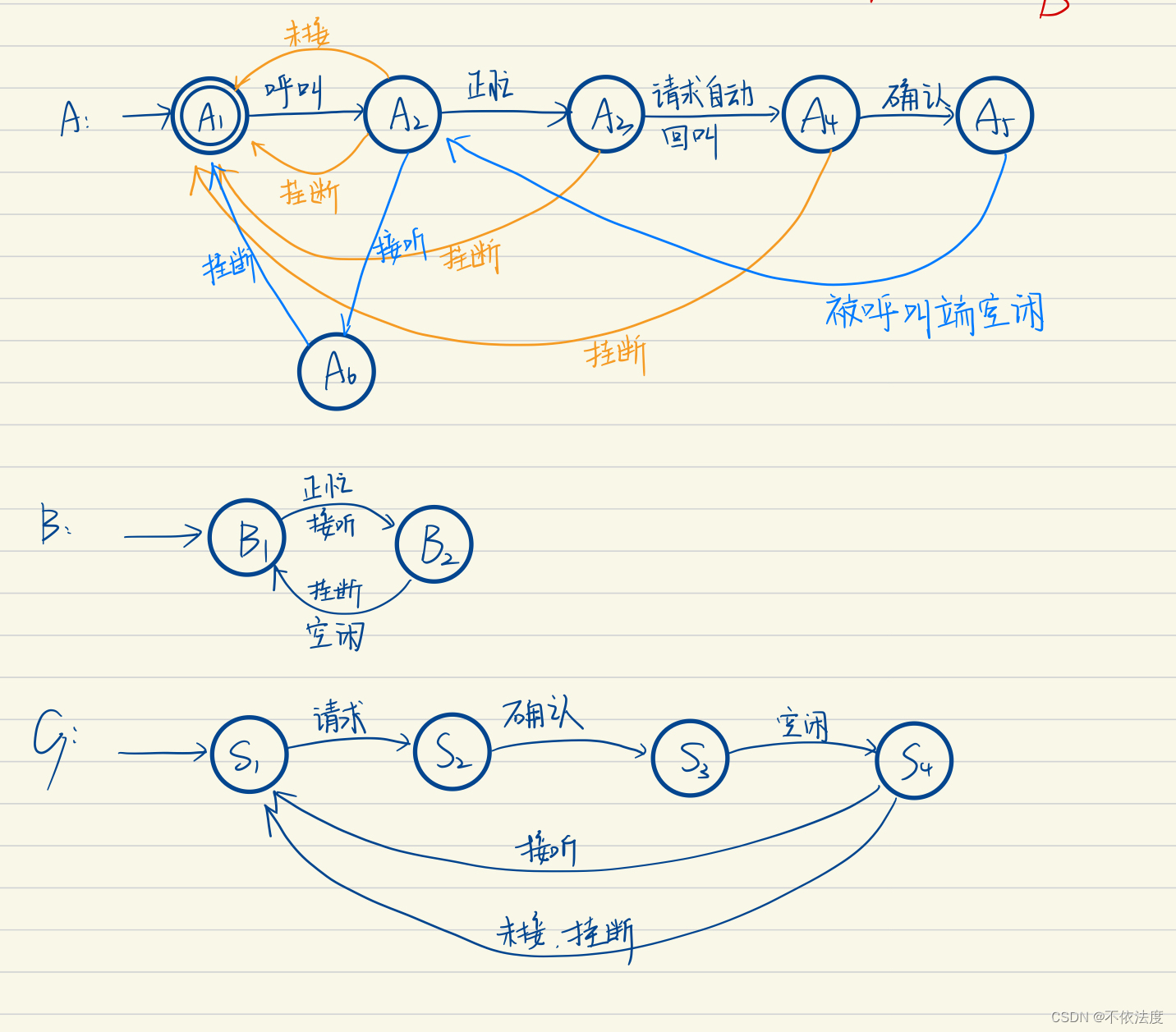
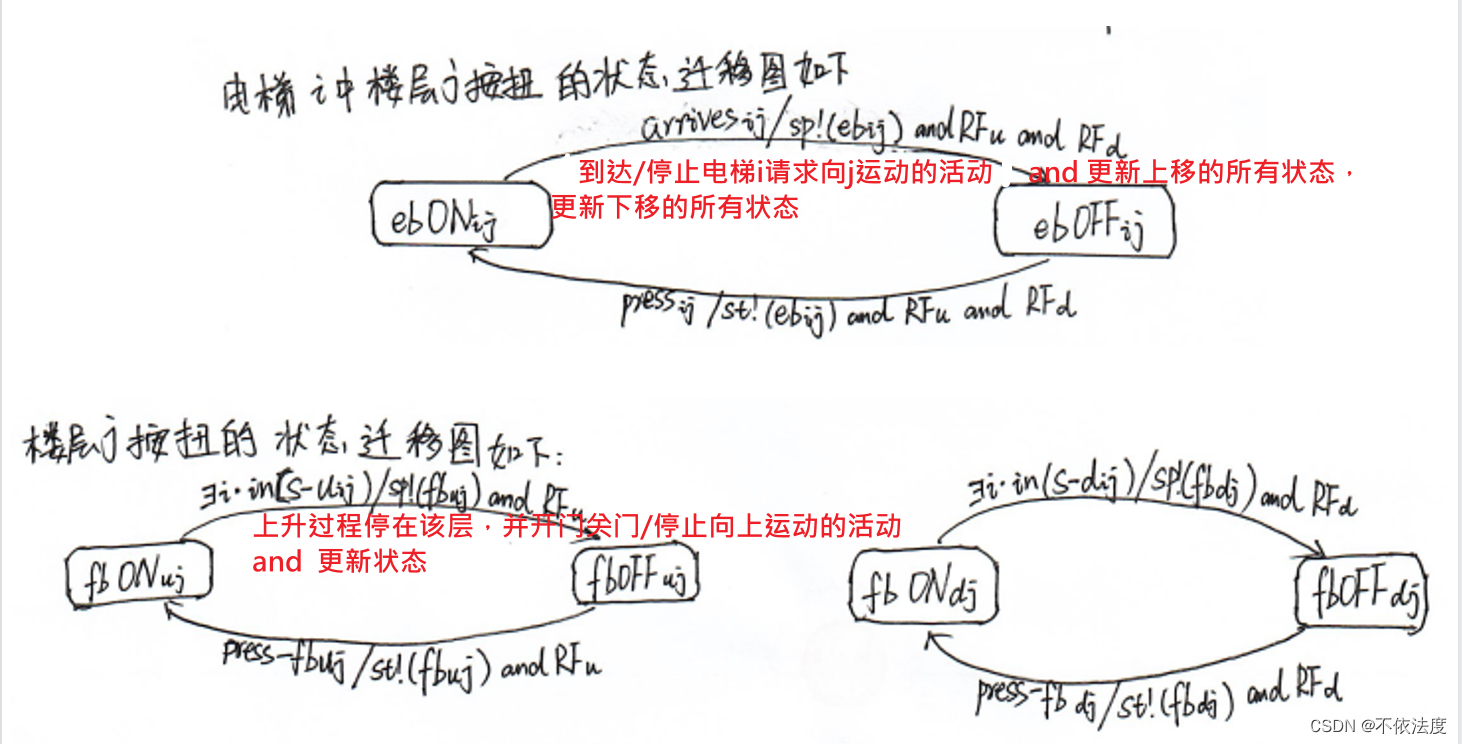
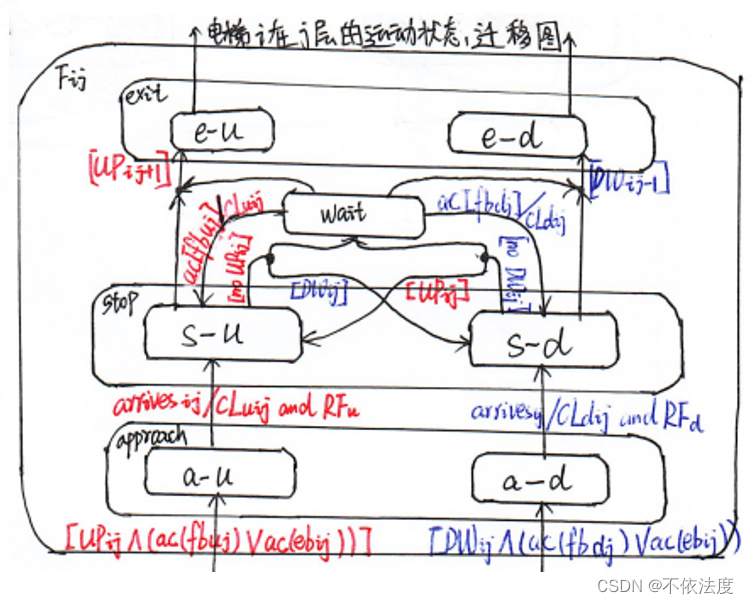
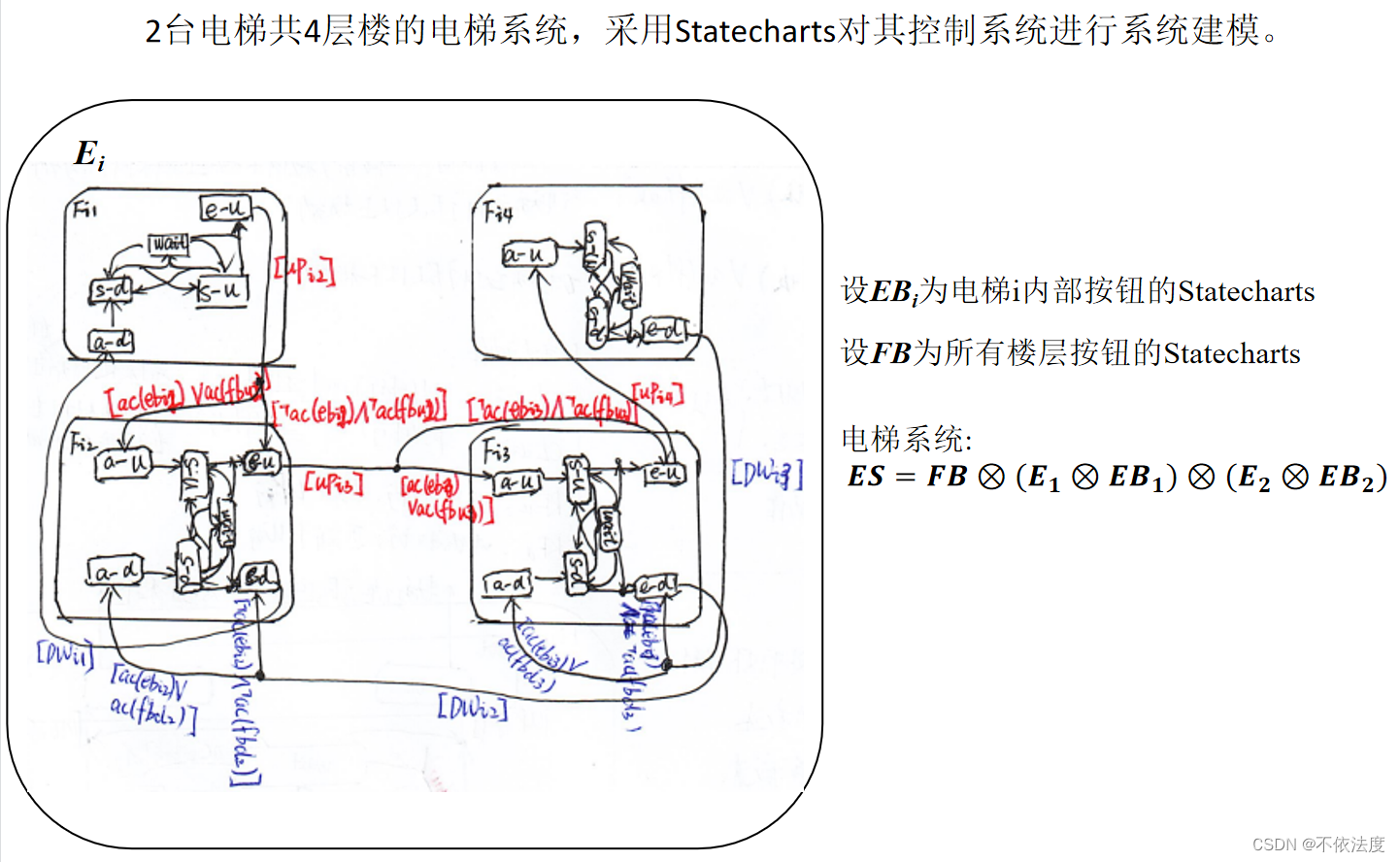
电梯控制系统
【考了,原题】
UPij和DWij用于判断是否有上行操作或者下行操作。(这样说更准确些)
这里 的 ‘/ ’ 不是或,/前面是实践(输入),后面是活动(输出)
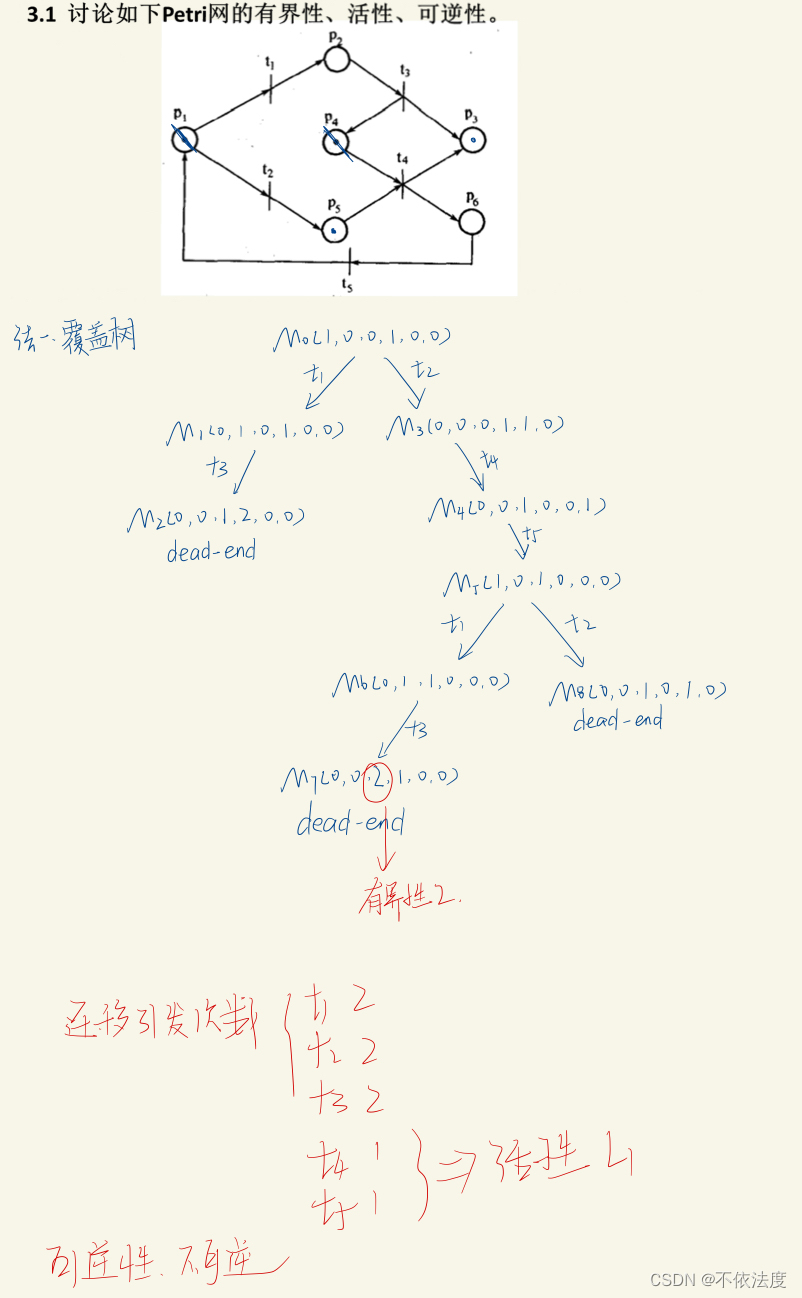
Petri网
Petri网概念
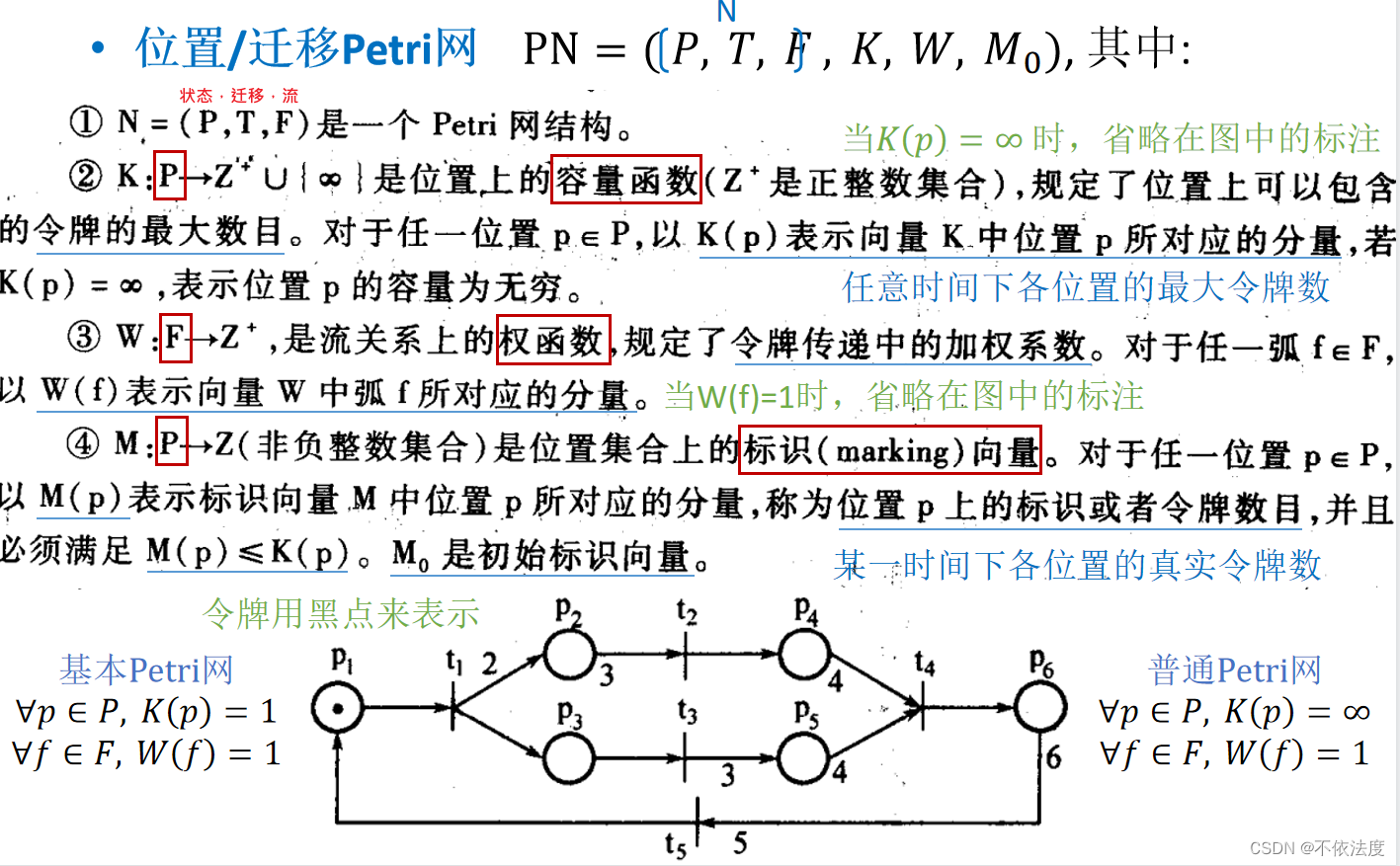
迁移的使能(可以理解为迁移的触发)
简单说就是迁移的所有输入流对应的状态圆圈,都拥有满足流权重的令牌数,即满足迁移触发的条件。
比如上图,t4触发的要求是P4有四个令牌且P5有四个令牌。
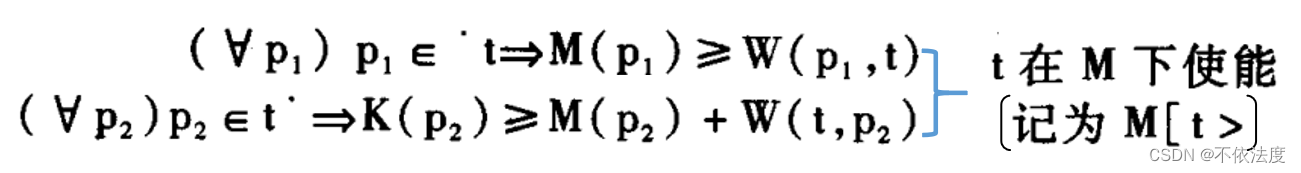
Petri网模型中四种关系
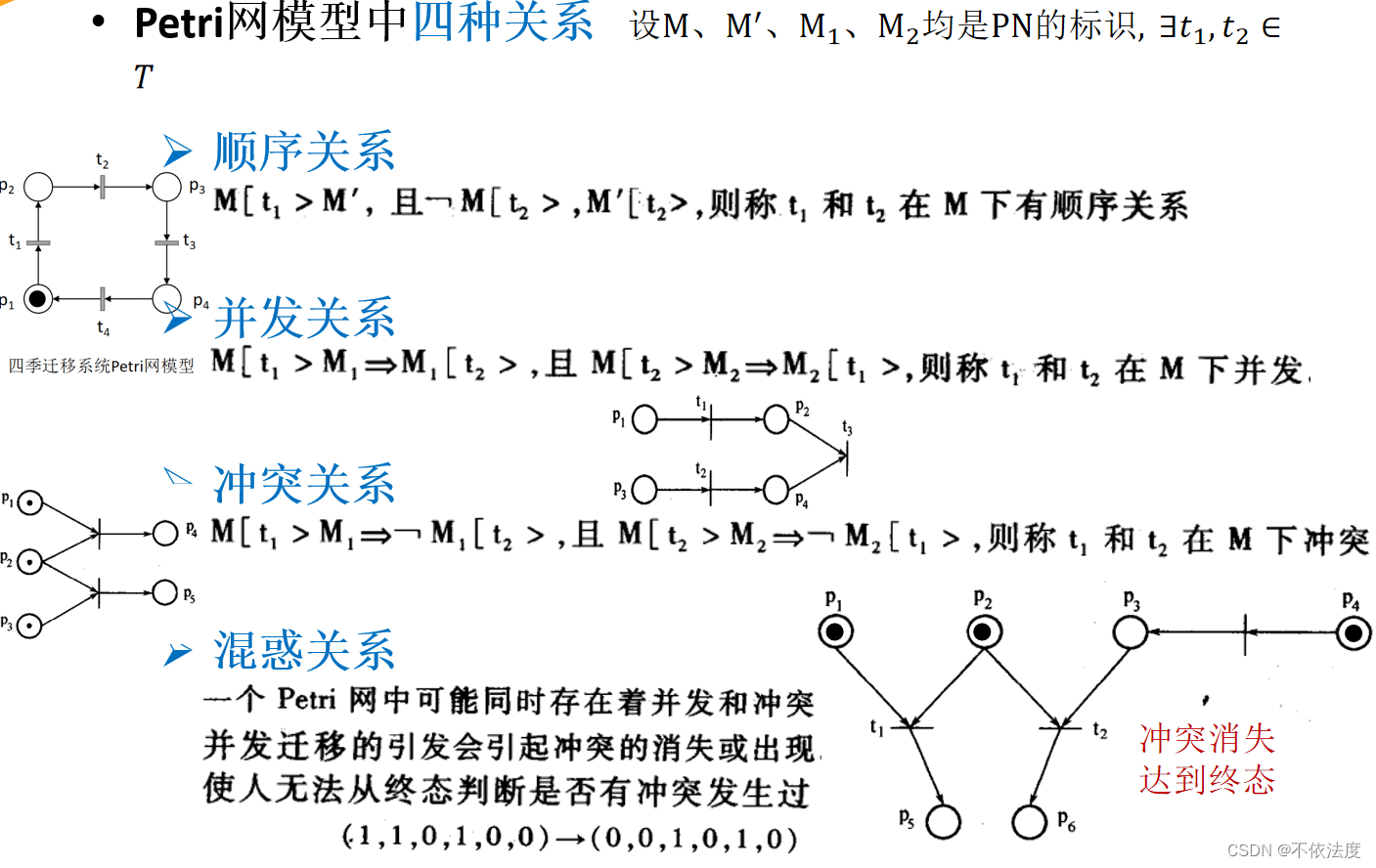
特殊Petri网
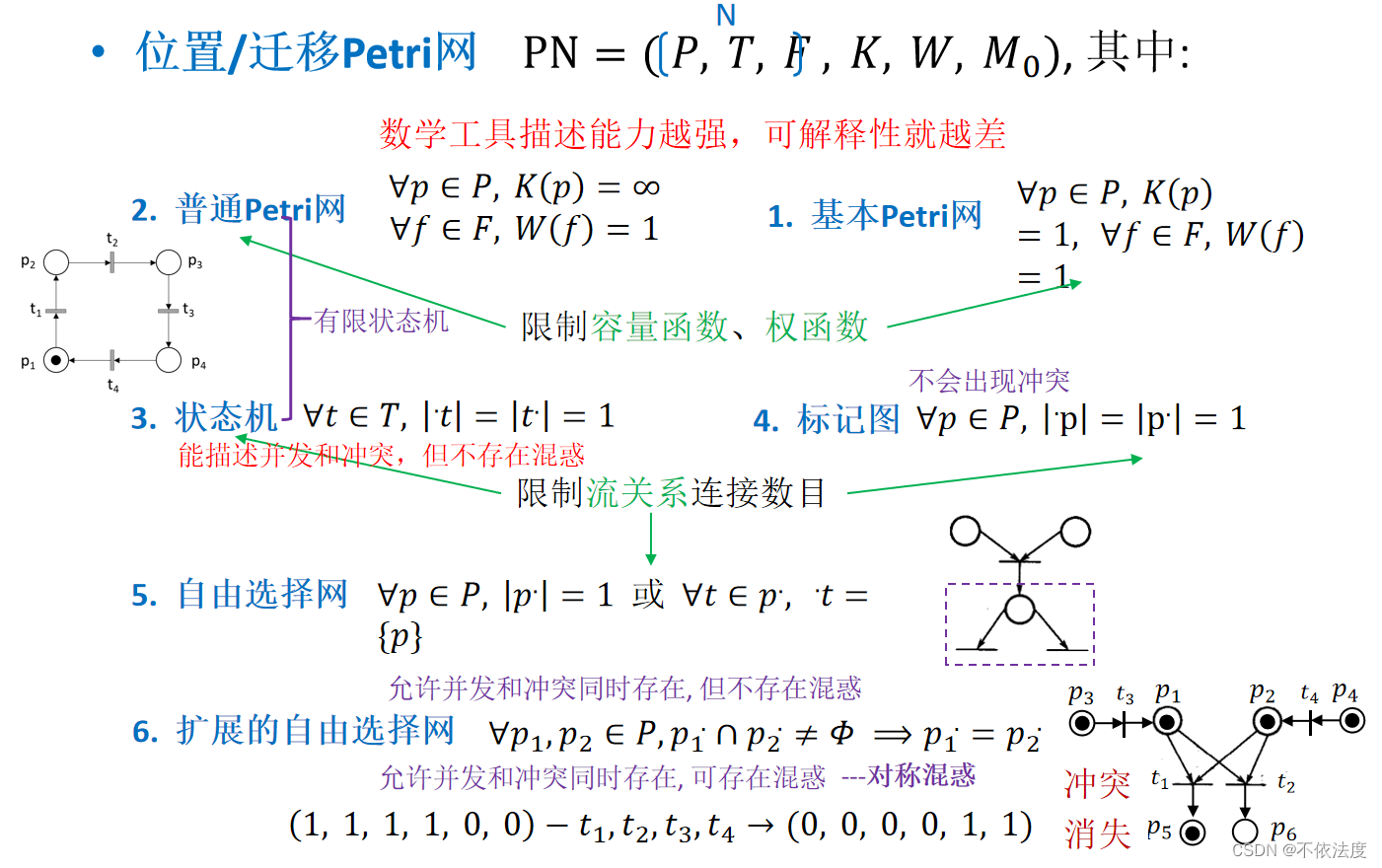
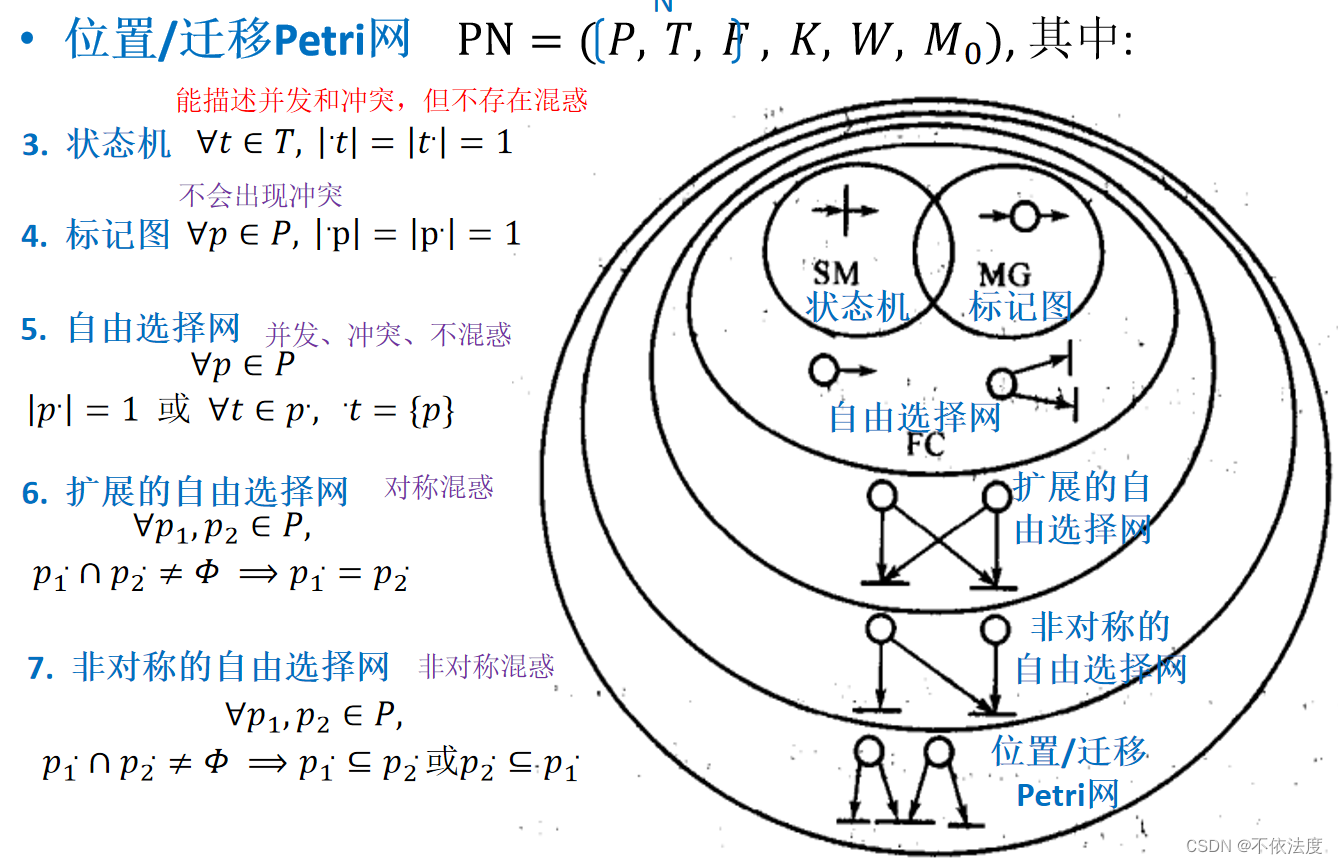
Petri网性质
-
可达性
- 若存在一个迁移引发序列σ, 使得初始标识符M0转换为Mn, 则称Mn是从M0可达的,记为M0[σ>Mn。
- 所有从M0可达的标识,组成可达标识集,记为R(N,M0)或R(M0)。
- 所有从M0出发的迁移引发序列,组成引发序列集,记为L(N,M0)或L(M0)。
-
有界性和安全性
- 若 ∃k∈N, 使得∀M∈R(M0)都有k≥M(p), 则位置p为k有界的。
- 若所有位置都是k有界的,则PN是k有界的。(有界性简单说就是最大的令牌数)
- 位置p为1有界,则称位置p是安全的。若所有位置都安全,则Petri网是安全的。
-
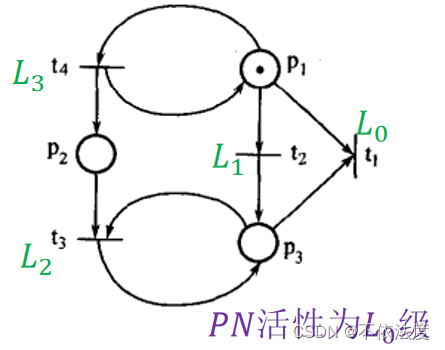
活性:迁移t的活性分为5级。(活性简单每个t最低活性等级)
- L0 : 任何迁移引发序列σ∈L(M0), 迁移t都不能引发。
- L1 : ∃σ∈L(M0), 迁移t至少引发一次 。
- L2 : 给定k≥2, ∃σ∈L(M0), 迁移t至少引发k次。
- L3 : ∃σ∈L(M0), 迁移t可以无限次地引发。
- L4 : ∀M∈R(M0),∃M′∈R(M),使得M′[t>。用语言说就是任意一个可能的引发序列中,t都可以引发无限次。
- 若∀t∈T,t的活性都在Li级及以上(i∈{0,1,2,3,4}),则称PN的活性为Li级
-
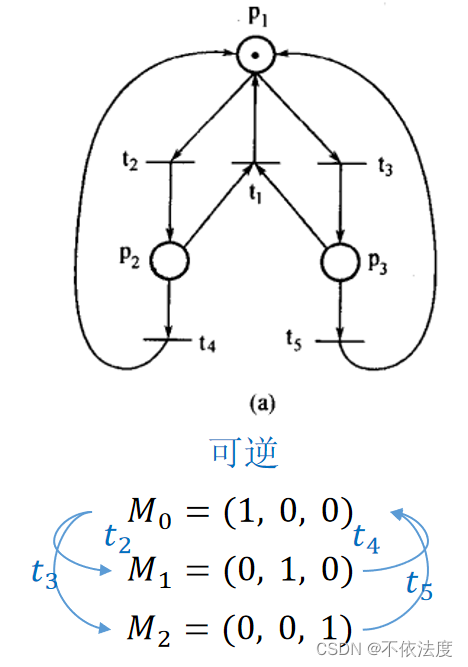
可逆性
- 若 ∀M∈R(M0), M0∈R(M), 则称该Petri网是可逆的。即所有状态都要回到指定状态(没有指定的话默认M0)。
- 顺便补充一下如何通过覆盖树看可逆,只要覆盖树的所有叶子节点都是M0就行
Petri网简化
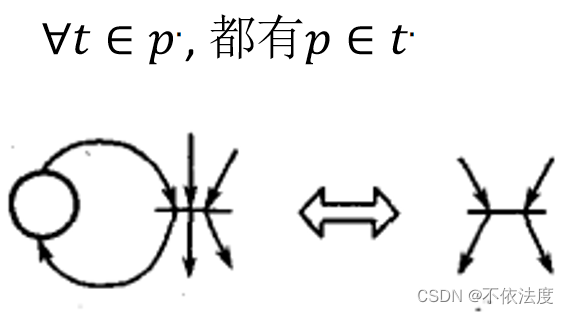
- 消除自循环位置
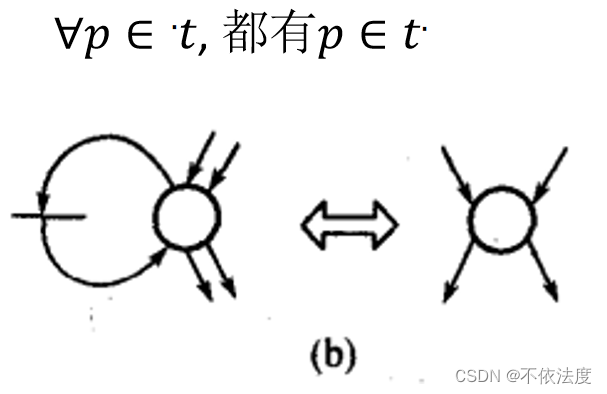
- 消除自循环迁移
- 合并串行位置
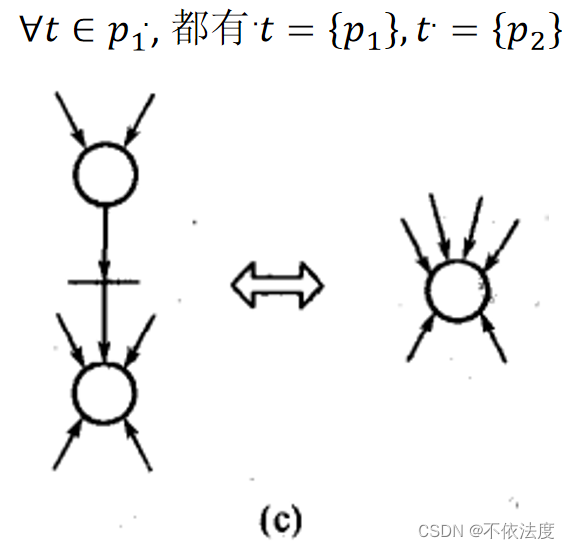
- 合并并行位置(权重也得相同)
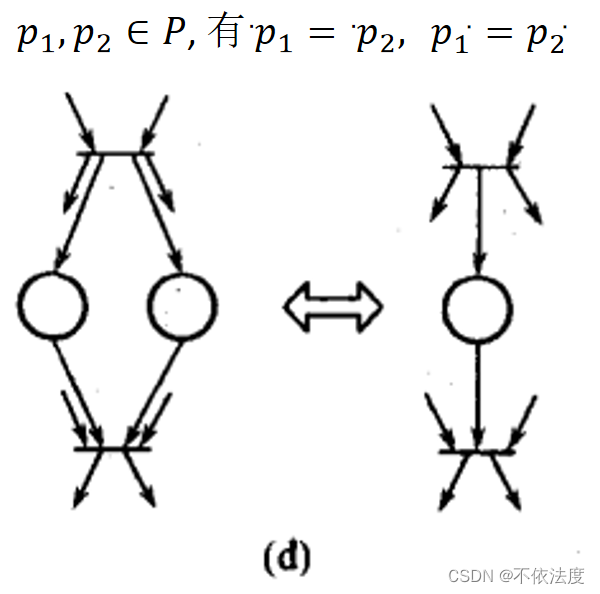
- 合并串行迁移
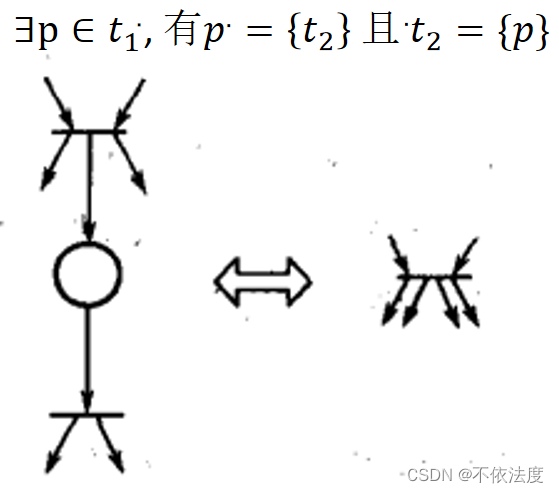
- 合并并行迁移(权重也得相同)
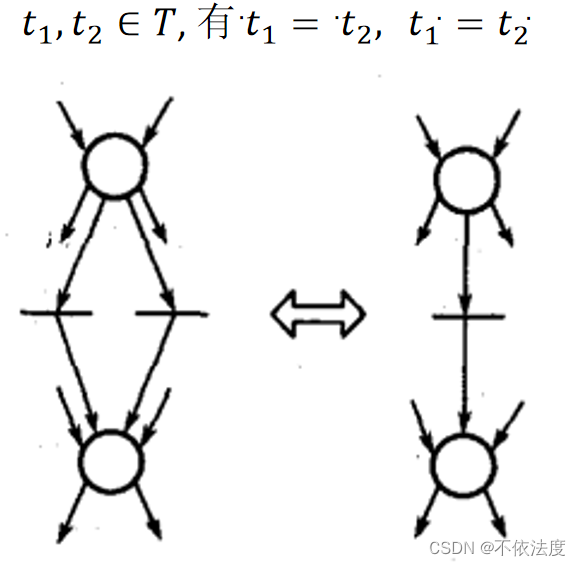
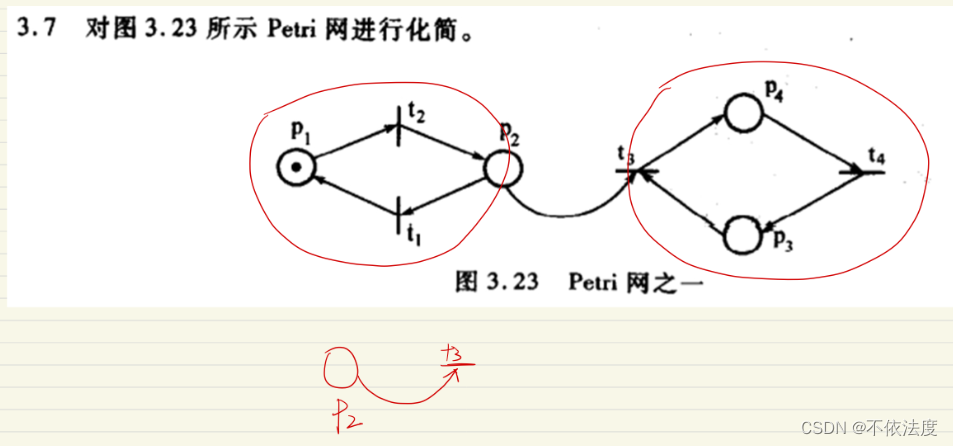
例题
简化后的P2上补个令牌。
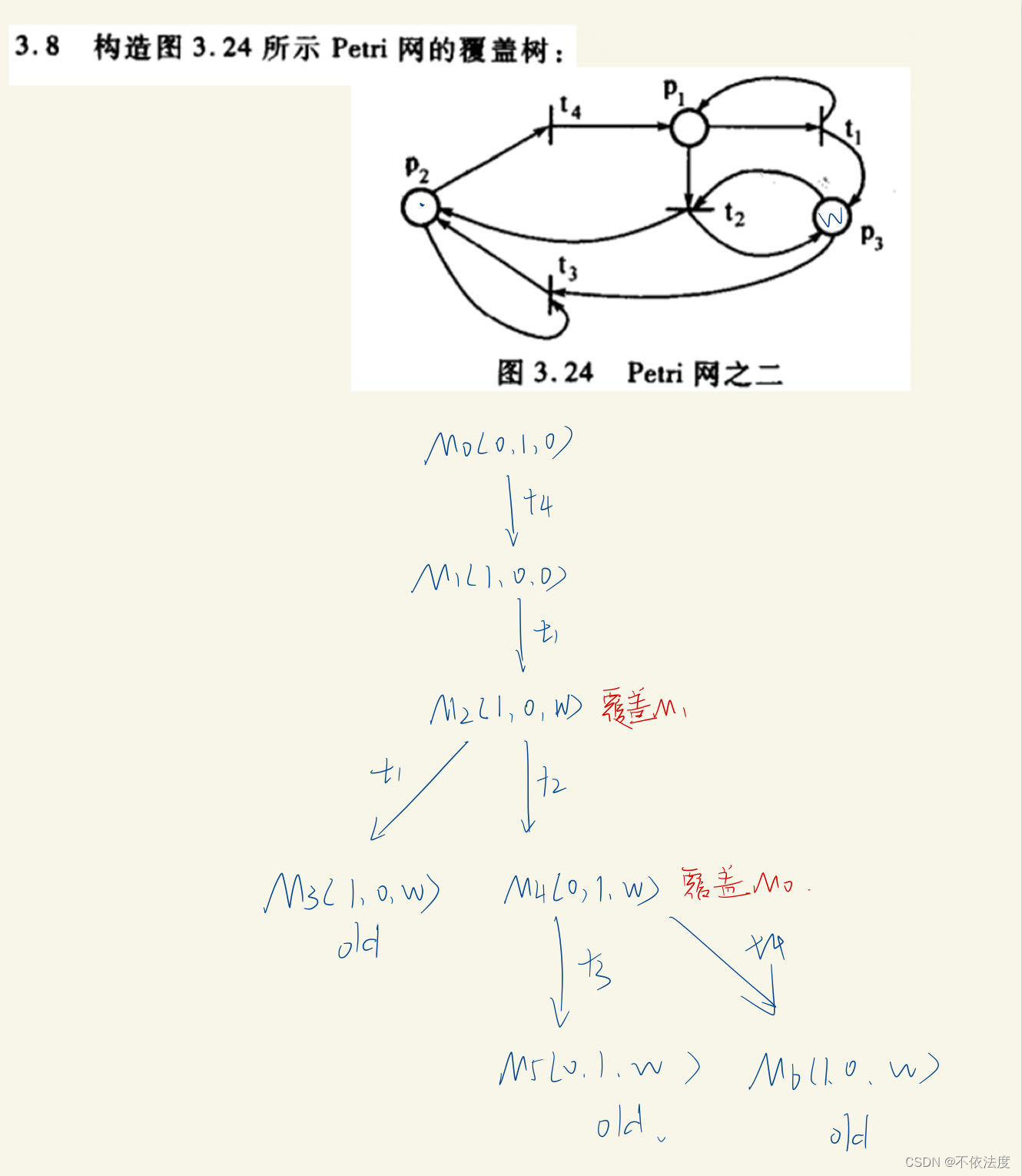
Petri网覆盖树
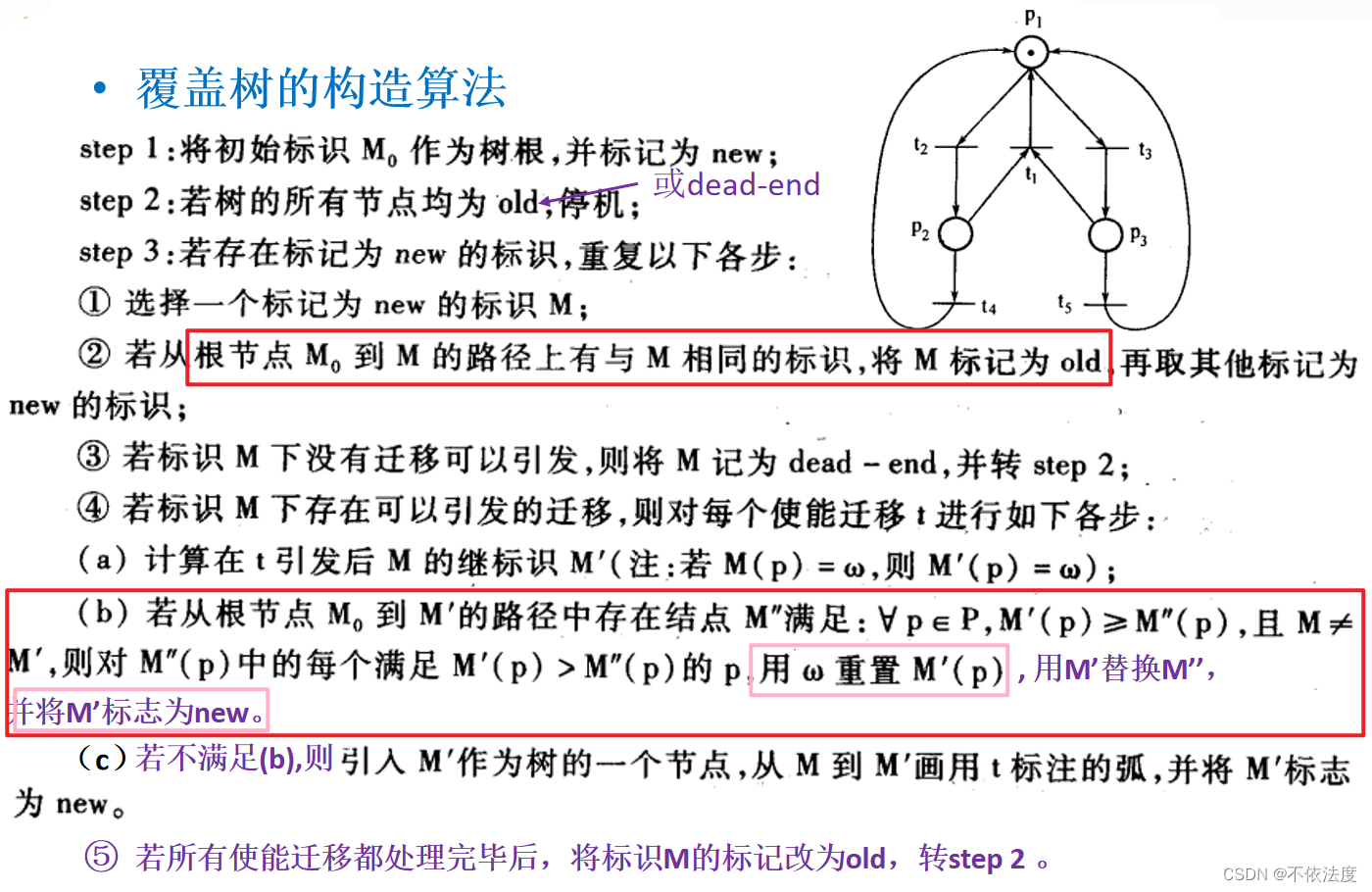
M’可以覆盖M即M’的每一个状态的令牌数都是大于等于M对应状态的令牌数。
比如M`=(0,1,0,2)就可以覆盖M=(0,0,0,1)。如果某一个覆盖存在部分状态的令牌数不同,其他的都相同,就可以把不同的令牌数用ω替换。比如(0,1,0,0)→ (0,2,1,0),(0,2,1,0)的第二,三个1就可以用ω替换,变成(0,ω,ω,0)。
顺便简单说一下原理:(0,2,1,0)是包含(0,1,0,0),那(0,2,1,0)中的(0,1,0,0)经过迁移会再次出现(0,2,1,0),这种迁移可以重复无限次,所以产生变化的令牌数可以无限次变化,增加,所以可以直接标为ω。
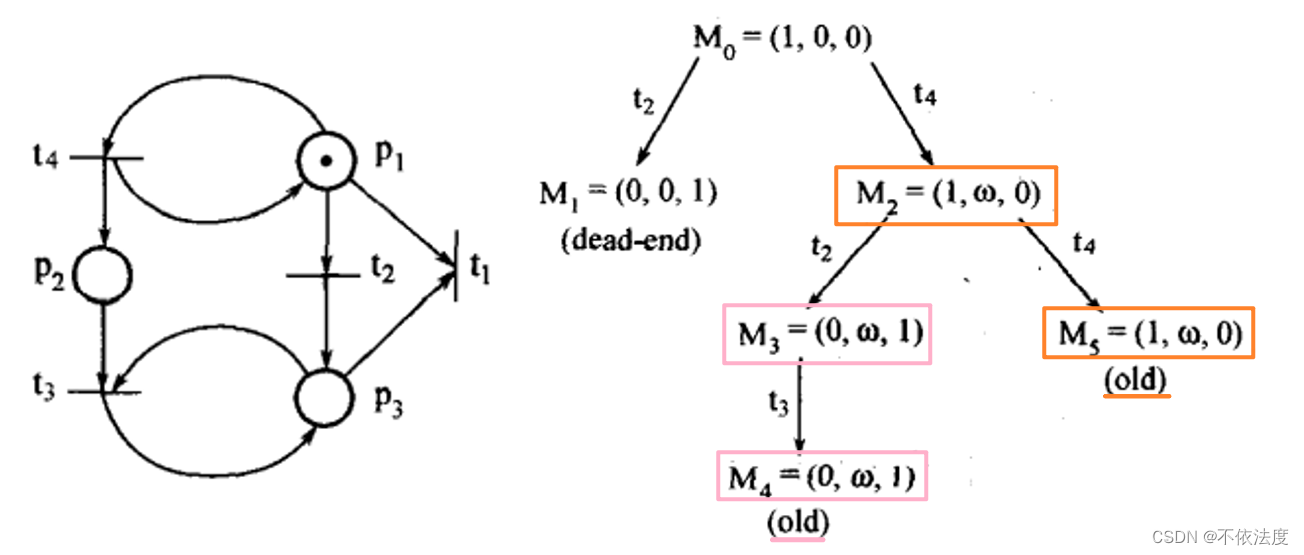
构造覆盖树
初始只有P2有令牌(P3的w忘擦了)
覆盖树分析Petri树性质

这题没有出现ω,所有比较好片段迁移引发德次数。
petri网构造
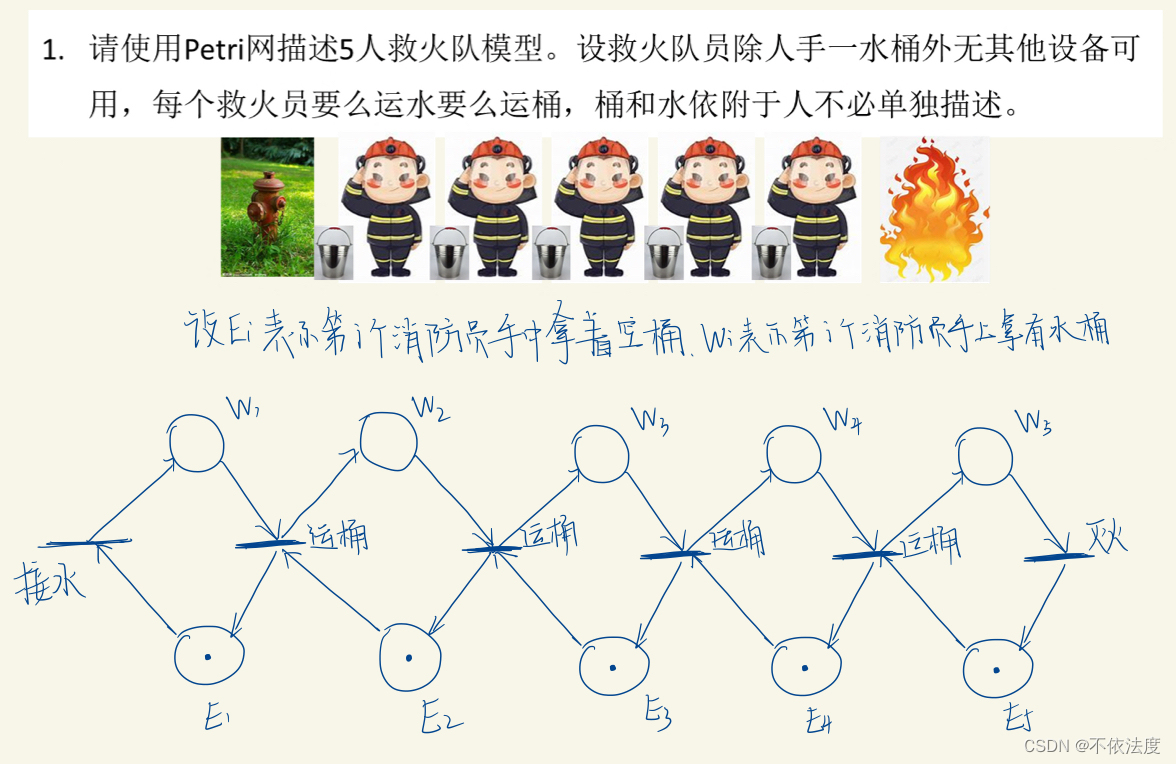
救火系统
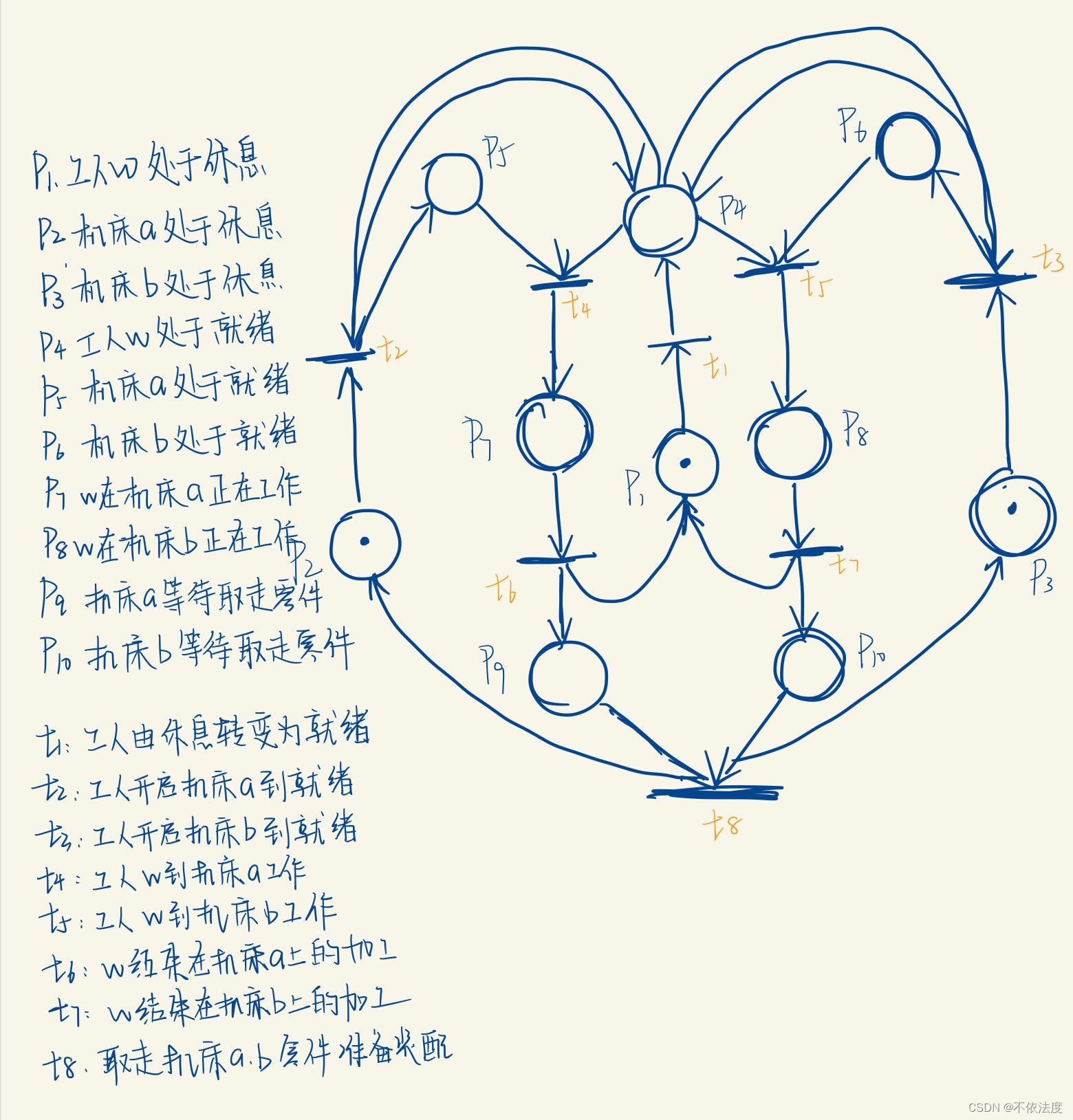
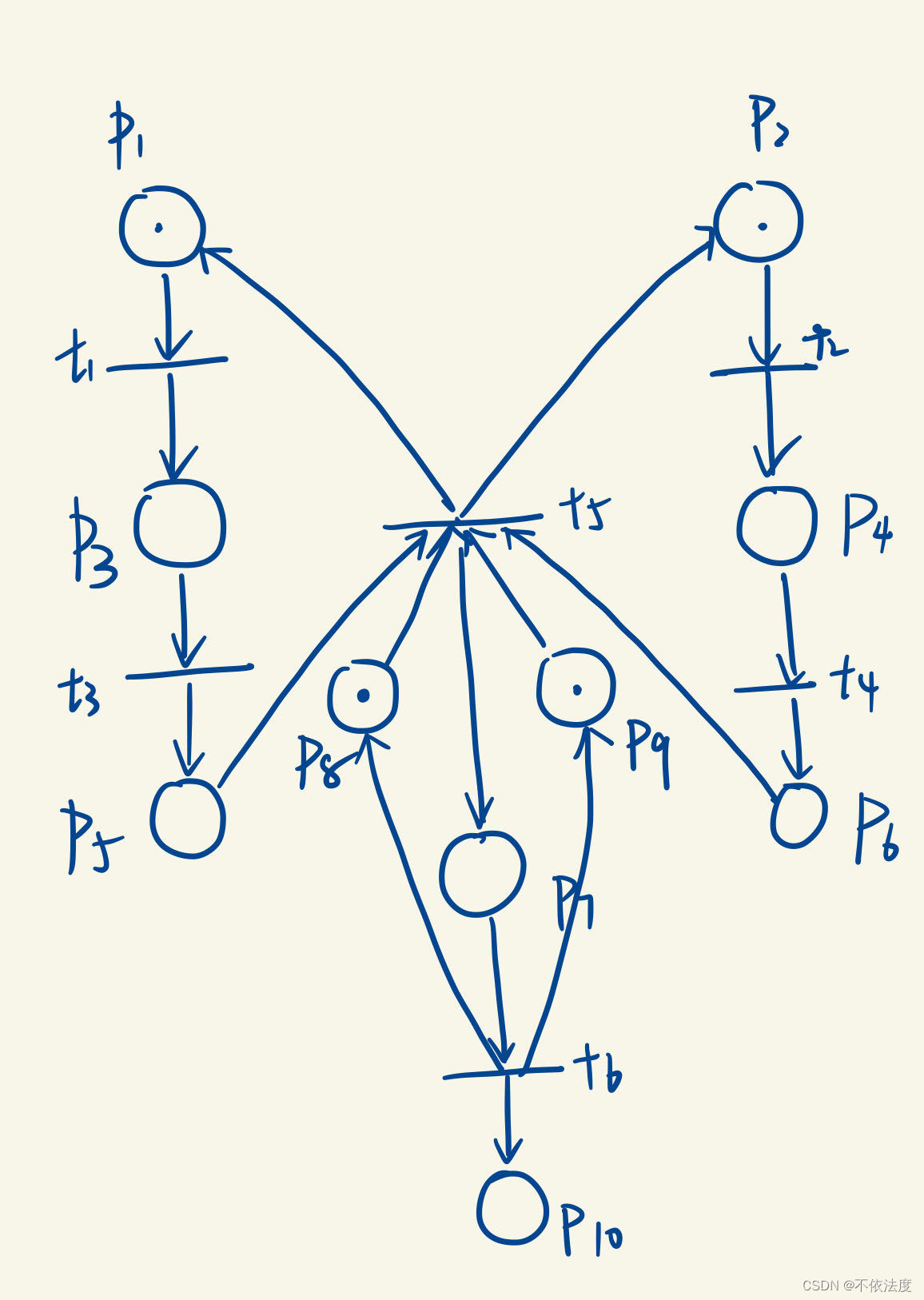
课后生产线
【考了,原题】
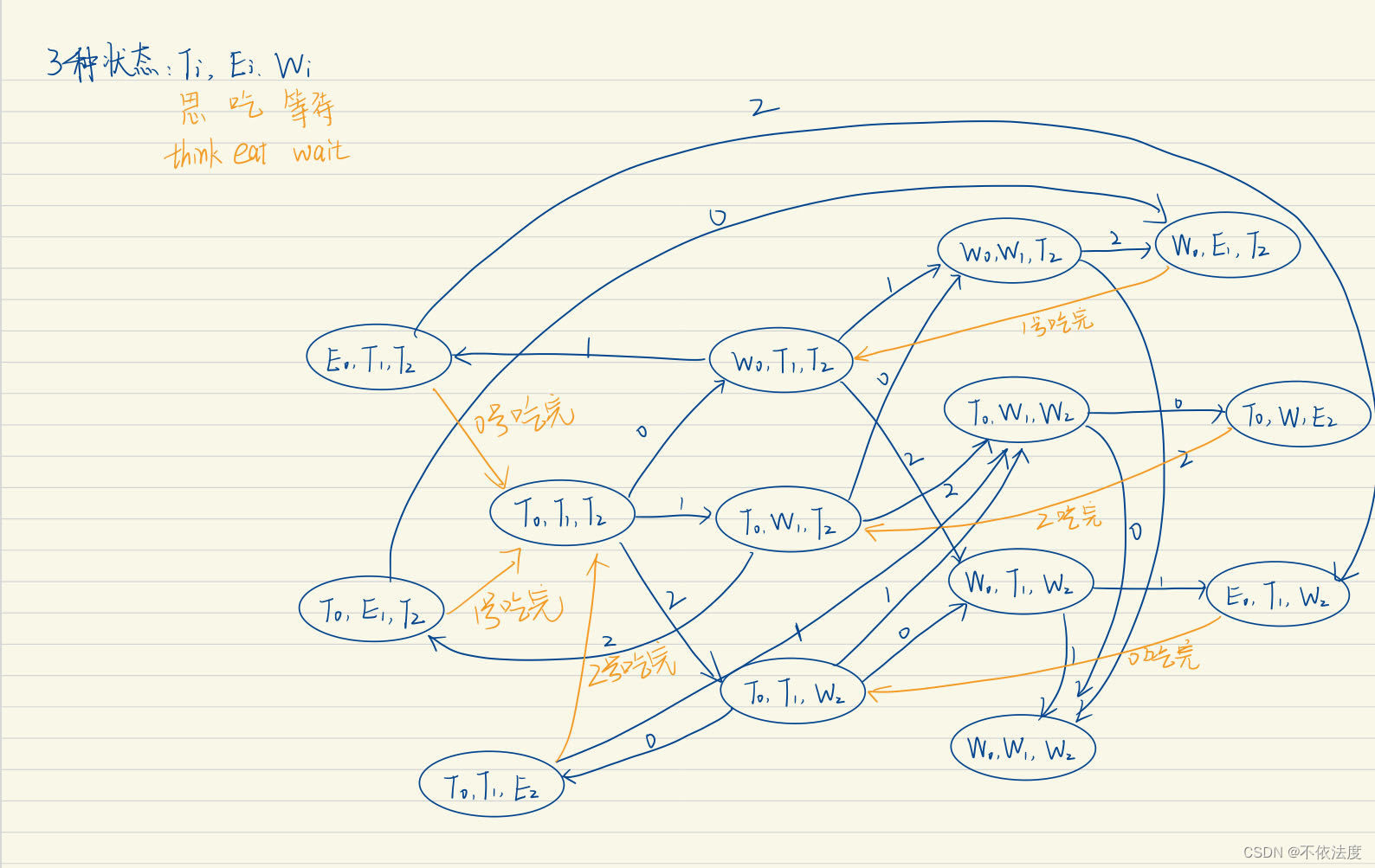
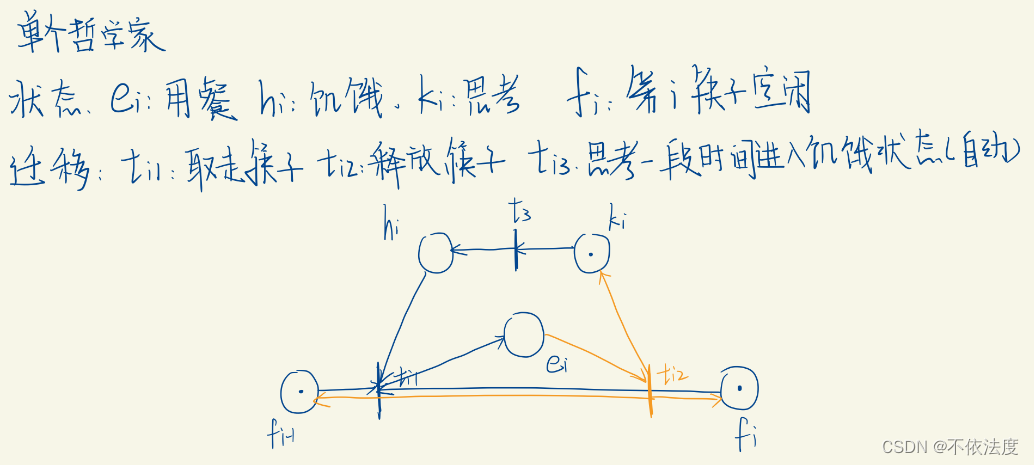
哲学家问题
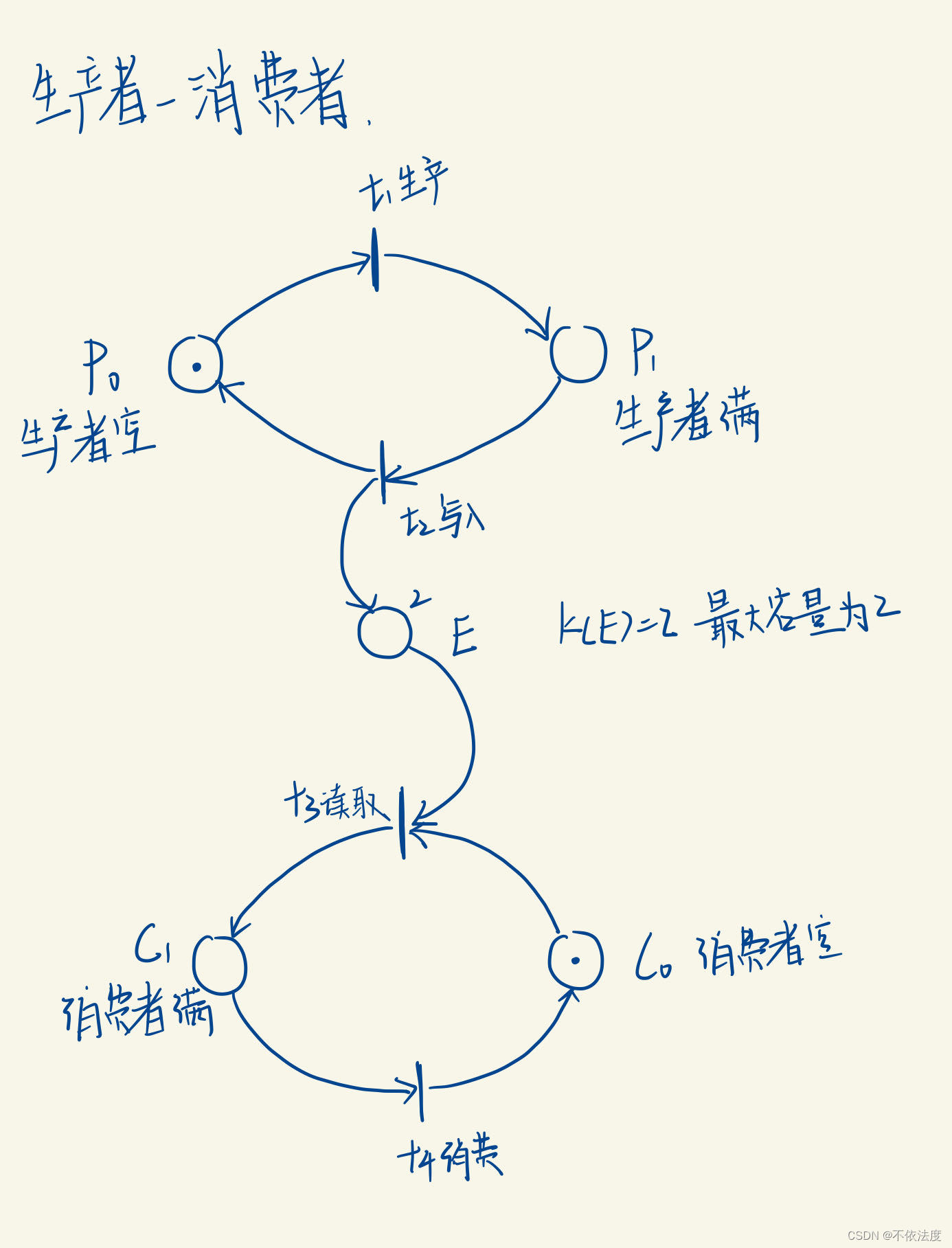
生产者-消费者问题
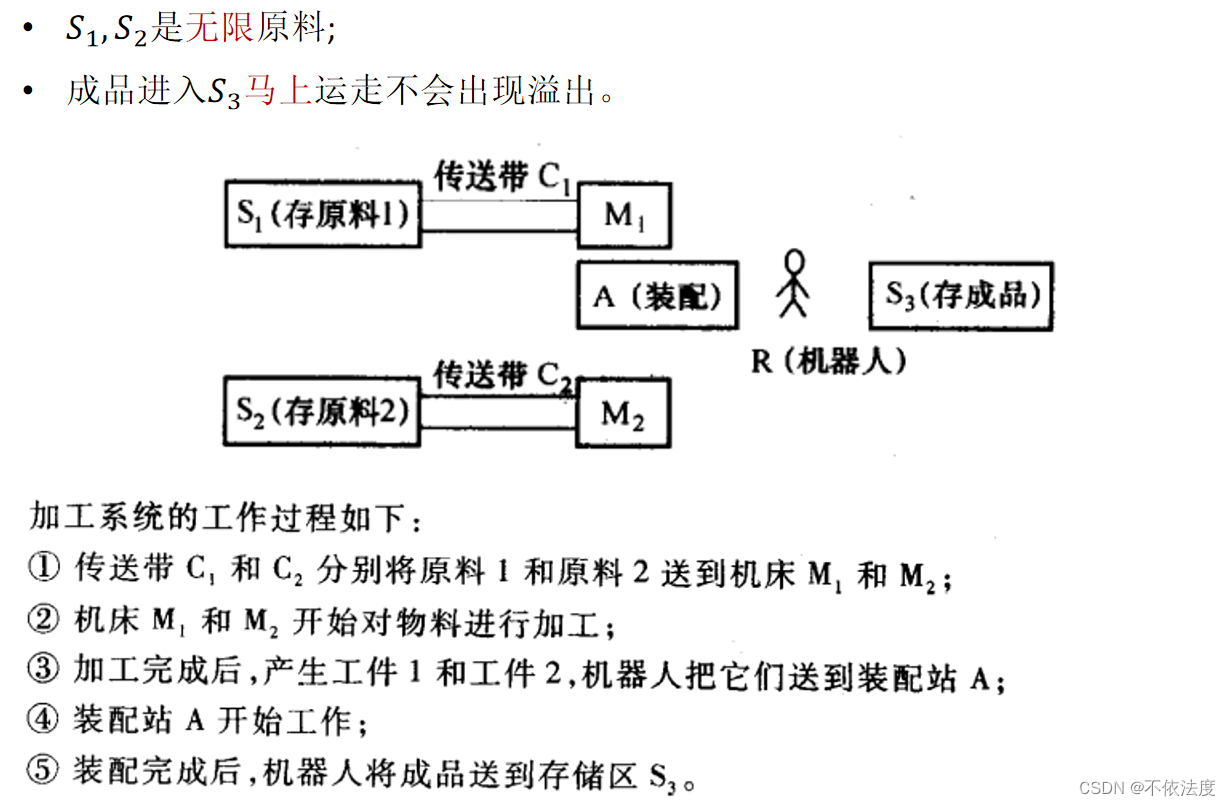
例题生产线










































 2689
2689











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








