DP小题单【2】

波风一一水门

已于 2022-08-06 10:47:16 修改

阅读量430

点赞数 4

分类专栏：笔记文章标签： c++ 算法动态规划

于 2021-11-23 12:46:06 首次发布

本文链接：https://blog.csdn.net/weixin_50909982/article/details/121474028

版权

笔记专栏收录该内容

56 篇文章 1 订阅

订阅专栏

题目列表见：DP小题单【1】
DP小题单【3】

单调队列维护窗口最值

acwing模板题
最大子序和
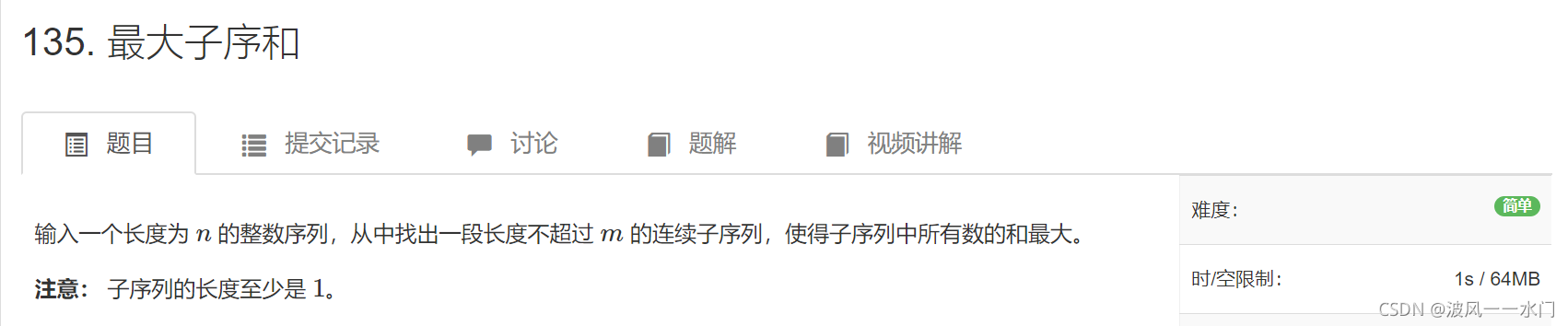
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int n,m;
const int N=3e5+10;
int a[N];
int q[N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        a[i]=a[i-1]+a[i];
    }
    int hh=0,tt=0;
    int sum=-0x3f3f3f3f;
    for(int i=1;i<=n;i++)
    {
        while(i-q[hh]>m)  hh++; 
        sum=max(sum,a[i]-a[q[hh]]);//更新当前状态：注意顺序
        while(hh<=tt&&a[i]<a[q[tt]])  tt--;//更新后边的状态
        q[++tt]=i;

    }
    cout<<sum<<endl;
}

修剪草坪
模板题2
在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
#define int long long
int a[N],q[N],f[N];
int g(int x)
{
    if(!x) return 0;
    return f[x-1]-a[x];
}
signed main () 
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        a[i]=a[i-1]+a[i];
    }
    int hh=0,tt=0;
    for(int i=1;i<=n;i++)
    {
        while(i-q[hh]>m) hh++;
        f[i]=max(f[i-1],g(q[hh])+a[i]);
        while(hh<=tt&&g(q[tt])<=g(i)) tt--;
        q[++tt]=i;
    }
    cout<<f[n]<<endl;
    return 0;
}

类似题：1088. 旅行问题 1089. 烽火传递 1090. 绿色通道

落谷：P5858 「SWTR-03」Golden Sword

题意：一个熔炉容量为 W , 给定 n 个原料扔进去锻造，每个材料都有权值 $a_i$ ，一个一个材料往里放，每个材料对答案 ans $的贡献是当前的原料个数*当前材料的权值a_i$ , 但是当前熔炉里的材料的个数是可以变化的，因为每次放入材料之前，我们都可以选择拿出不超过 s 个原料——来更好的利用熔炉的空间，求ans的最大值。
输入： $n , w , s 和 a_i$ 如上描述。
~~看眼代码，思路紧跟其后：~~

#include <algorithm>
#include<cstring>
#include <iostream>
using namespace std;
#define int long long
const int N = 5e3 + 10;
int dp[N][N],a[N],n,w,s;
int q[N];
//int g[N];可以搞个数组存函数值，也可以像下边一样开个函数
int g(int i,int x)
{
    return dp[i-1][x];
}
signed main()
{
    cin>>n>>w>>s;
    for(int i = 1; i <= n ;i ++)
        scanf("%lld",&a[i]);
    memset(dp,-0x3f,sizeof dp);
    dp[0][0] = 0;
    for(int i = 1; i <= n ;i ++)
    {
        int hh = 0,tt = 0;
        q[hh] = w;// j 滑动的范围
        //g[hh] = dp[i-1][w];//放m进来是因为之后放入队列的下标就是m-1开始了 
        for(int j = w ; j >= 1; j--)
        {
            while(hh<=tt&&q[hh]>j+s-1) hh++;
            while(hh<=tt&&g(i,q[tt])<dp[i-1][j-1]) tt--;
            q[++tt] = j - 1;
            //g[tt] = dp[i-1][j-1];
            dp[i][j] = g(i,q[hh]) + j * a[i];
        }
    }
    int ans=-0x3f3f3f3f;
    for(int i = 1 ;i <= w ; i++)
    {
        ans =  max(ans , dp[n][i]);
    }
    cout<<ans<<endl;
}

这道题也是一道单调队列优化DP的板子题，先讲讲DP的思路。
$状态表示： f [i] [j] 表示前 i 个数，当前锅中原料个数为 j 的最大值$
$状态转移： f [i] [j] = f [i - 1] [k] + a [i] * j ， k \in [j - 1, j + s - 1]$
状态表示很好想。转移的话，最简单的思路就是不往外拿， $f [i] [j] 肯定是 f [i - 1] [j - 1] 放入了一个新元素转移过来的$ 。然后再就是前一个元素拿出了 k 个元素，然后放入了当前元素也可以转移过来。右边界有一个减一的原因是先当前这个材料必选（稍想一想）。
这道题的单调队列是维护的前一维的状态，和前两个题不同，前两个题都是当前这一维的，而且这个题还要维护的是 j 下标后边的一段窗口，你正向遍历体积的话一开始都没有状态可以转移过来，所以我们必须要倒着遍历体积。
$q [hh] 初始值为 w, 每次维护前一维的 d p [i - 1] [j - 1], 这样我们才能保证遍历到 d p [i] [j] 的时候, d p [i - 1] [j - 1] 到 d p [i - 1] [j + s - 1] 全部被更新到了。$

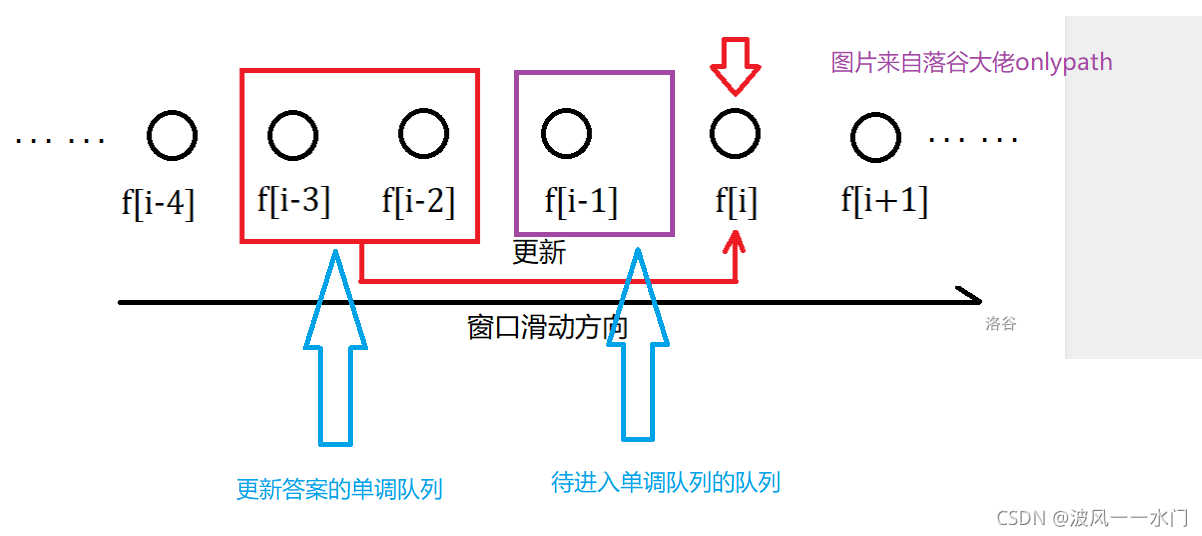
两个单调队列维护区间最值

为啥需要两个单调队列呢，因为有些题需要维护区间最值，这个区间是在下标 i 的同一侧，这样一个单调队列维护起来比较麻烦，可以用两个单调队列倒腾一下。一个存是单调队列，一个是待进入单调队列里的队列，分别维护窗口的两个边界。
在这里插入图片描述

P1725 琪露诺
题意就是维护这样一个区间最值：
在这里插入图片描述
我知道线段树等等高级数据结构都可以 $n*log_n$ 解决这个问题，但是单调队列的时间复杂度 $O (n)$ 岂不更好。~~其实就是不会那些数据结构。~~
细节都放注释里了，不多赘述：

#include<bits/stdc++.h>
using namespace std;
const int N=500010;
#define int long long
int n,l,r;
int f[N];
int q[N];//单调队列
int qq[N];//待进入单调队列的元素
int a[N],w[N],pos[N];//pos是第一个队列到第二个队列的下标映射
void solve()
{
    f[0]=0;
    int h=1,t=0;
    int hh=1,tt=0;
    qq[++tt]=0;
    for(int i=1;i<=n+r;i++)
    {   //cout<<"!";
        //cout<<hh<<endl;
        while(i-qq[hh]>r&&hh<=tt)  hh++;//先判不越界
        while(i-qq[hh]>=l&&i-qq[hh]<=r&&hh<=tt)
        {//如果待入队元素合法，把队头加到单调队列之中
            while(f[qq[hh]]>=q[t]&&h<=t) t--;
            q[++t]=f[qq[hh]];//加入合法队头
            pos[t]=qq[hh];//用pos数组将第一个队列的下标对应到数组下标
            hh++;//第二个队列用一个数，后移一个数——单调
        }
        while(i-pos[h]>r&&h<=t)  h++;
        if(h<=t)//如果第一个队列合法直接取出队头元素更新答案
        {
            qq[++tt]=i;//当前元素加入第二个队列
            f[i]=max(f[i],q[h]+a[i]);
        }
    }
}
signed main()
{
    cin>>n>>l>>r;
    memset(f,-0x3f,sizeof f);
    for(int i=0;i<=n;i++)
    {
        cin>>a[i];
    }
    solve();
    int ans=-0x3f3f3f3f;
    for(int i=n+1;i<=n+r;i++)  ans=max(ans,f[i]);
    cout<<ans<<endl;
}

一样思路的题目：P3957 [NOIP2017 普及组] 跳房子

单调队列维护窗口+二分。

#include<bits/stdc++.h>
using namespace std;
const int N=500010;
#define int long long
int n,d,k;
int f[N];
int q[N];//单调队列
int qq[N];//待进入单调队列的元素
int a[N],w[N],pos[N];//pos是第一个队列到第二个队列的下标映射
bool check(int g)
{
    f[0]=0;
    int s,r;//分别代表改进之后可以跳的范围
    if(g<d)  s=d-g,r=d+g;
    else  s=1,r=d+g;
    int h=1,t=0;
    int hh=1,tt=0;
    qq[++tt]=0;
    for(int i=1;i<=n;i++)
    {
        while(a[i]-a[qq[hh]]>r&&hh<=tt)  hh++;//先判不越界
        while(a[i]-a[qq[hh]]>=s&&a[i]-a[qq[hh]]<=r&&hh<=tt)
        {//如果待入队元素合法，把队头加到单调队列之中
            while(f[qq[hh]]>=q[t]&&h<=t) t--;
            q[++t]=f[qq[hh]];//加入合法队头
            pos[t]=qq[hh];//用pos数组将第一个队列的下标对应到数组下标
            hh++;//第二个队列用一个数，后移一个数——单调
        }
        while(a[i]-a[pos[h]]>r&&h<=t)  h++;
        if(h<=t)//如果第一个队列合法直接取出队头元素更新答案
        {
            qq[++tt]=i;//当前元素加入第二个队列
            f[i]=max(f[i],q[h]+w[i]);
            if(f[i]>=k) return true;
        }
    }
    return false;
}
signed main()
{
    cin>>n>>d>>k;
    int sum=0;
    for(int i=1;i<=n;i++) 
    {
        cin>>a[i]>>w[i];
        if(w[i]>0) sum+=w[i];
    }
    if(sum<k)  cout<<-1<<endl;
    else 
    {
        int l=0,r=2e9;
        while(l<r)
        {
            int mid=l+r>>1;
            memset(f,-0x3f,sizeof f);
            if(check(mid))//如果可以的到k的分数就可能缩小边界
            {
                r=mid;
            }
            else//如果得不到的话一定增大边界
            {
                l=mid+1;
            }
        }   
        cout<<l<<endl;
    }
}

线性DP

D - Decelerating Jump

D - Decelerating Jump——利用单调性优化DP

题意：给定一个串：在这里插入图片描述
你必须从1 号点出发，跳落在 n 号点，你条的步数的轨迹必须是单调递减的（非严格），求在跳的过程中得到的最大分数？
比如样例可以跳2步再跳1步，获得最大分数 3 。
这道题最暴力的方法是可以定义 $f [i] [j]$ 为当前位置是 $i$ ，前一步由 $j$ 跳过来的最大分数。这样的话，对于任何一个点对 $f [i] [j]$ ，都要枚举它前一维的状态。
即： $f [i] [j] = ma x (f [i] [j], f [i - j] [k], k >= j$ ，这样时间复杂度是 $n^3$ 的。
对于这样一个式子，我一开始想单调队列优化，但是这道题如果用这种状态表示的话根本就无法用单调队列优化来做，此时我们就应该换种思路，而不是继续想怎么优化。
$定义 f [i] [j] 表示前 i 个数, 跳到 i 这个位置最少的一步是 j$
为什么这个状态的步数要定义为最少的呢？
因为如果是最少就有了单调性，也就是说它之前跳过来的步数肯定比当前步数要大。
因为我们可以开一个 $d p [i]$ 数组维护此时此刻的 $f [i] [j]$ ，然后先遍历 $j$ ,让 $j$ 从大到小枚举，使得 $d p [i - j]$ 中存的 $f [i] [k]$ 的值， $k$ 总是大于等于当前枚举的 $j$ 。（这个不理解看一眼代码就知道了），这样就可以直接拿过来更新当前状态了。

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5010;
int f[N][N],a[N],dp[N];
int n , m;
signed main()
{
    cin>>n;
    for(int i = 1;i<=n;i++)  cin>>a[i];
    for(int i = 1; i <=n ;i ++)
    {
        for(int j = 1 ;j<=n ;j++)
        {
            f[i][j] = -1e18;
        }
        dp[i] = -1e18;
    }
    dp[1] = a[1];
    for(int j = n - 1; j >=1 ; j--)
    {
        for(int i = 1; i <= n; i++)
        {
            if(i-j>=1)
            f[i][j] = max(f[i][j],dp[i-j] + a[i]);
            dp[i] = max(dp[i], f[i][j]);
        }
    }
    int res = -0x3f3f3f3f3f3f3f;
    for(int i = 1;i <= n; i++)
    {
        res = max(res , f[n][i]);
    }
    cout<<res<<endl;
}

P1052 [NOIP2005 提高组] 过河
~~此题没证明明白，日后再想qaq~~

四位数组线性递推——P1541 [NOIP2010 提高组] 乌龟棋
当前位置 now 别忘了加1 ，起点是1。

#include<bits/stdc++.h>
using namespace std;
const int N = 50;
int mp[50];
int a[400];
int g[N][N][N][N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)  cin>>a[i];
    for(int i=1;i<=m;i++)  
    {
        int x;
        cin>>x;
        mp[x]++;
    }
    g[0][0][0][0]=a[1];
    for(int i1=0;i1<=mp[1];i1++)
    {
        for(int i2=0;i2<=mp[2];i2++)
        {
            for(int i3=0;i3<=mp[3];i3++)
            {
                for(int i4=0;i4<=mp[4];i4++)
                {
                    int now =1+ i1*1 + i2*2 + i3*3 + i4*4;
                    if(i1!=0)  g[i1][i2][i3][i4]=max(g[i1][i2][i3][i4],g[i1-1][i2][i3][i4]+ a[now]) ;
                    if(i2!=0)  g[i1][i2][i3][i4]=max(g[i1][i2][i3][i4],g[i1][i2-1][i3][i4]+ a[now]) ;
                    if(i3!=0)  g[i1][i2][i3][i4]=max(g[i1][i2][i3][i4],g[i1][i2][i3-1][i4]+ a[now]) ;
                    if(i4!=0)  g[i1][i2][i3][i4]=max(g[i1][i2][i3][i4],g[i1][i2][i3][i4-1]+ a[now]) ;
                }
            }
        }
    }
    cout<<g[mp[1]][mp[2]][mp[3]][mp[4]]<<endl;
}

最大k子矩阵和
在这里插入图片描述
题意：给定长度为 n 的序列，让你找出其中 k 个连续子段（两个子段可以有公共端点），求子段和最大值。
状态划分：
$i 这个点选或不选$
状态表示：
$f [i] [j] [x] 表示前 i 个数选择划分 j 部分且当前这个元素选或不选（ x = 1 或 x = 0 ）$
状态转移:比较好想，不多赘述。

#include<bits/stdc++.h>
#define int long long
const int N=5010;
int f[N][N][5],n,m;
int a[N];
using namespace std;
signed main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)  
    {
        cin>>a[i];
    }
    memset(f,-0x3f,sizeof f);
    f[0][0][1]=f[0][0][0]=0;
    for(int i=1;i<=n;i++) f[i][0][1]=a[i];
    for(int i=1;i<=n;i++)
    f[i][0][0]=0;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
           f[i][j][1]=max(f[i][j][1],f[i-1][j][1]+a[i]);
           f[i][j][1]=max(f[i][j][1],max(f[i-1][j-1][1],f[i-1][j-1][0])+a[i]);
           f[i][j][0]=max(f[i][j][0],max(f[i-1][j][0],f[i-1][j][1]));
        }
    }
    int res=-0x3f3f3f3f3f3f3f;
    res=max(f[n][m][1],f[n][m][0]);
    cout<<res<<endl;
}

P1941 [NOIP2014 提高组] 飞扬的小鸟
两种背包，线性递推。

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
int f[N][2005];
int st[N];
int n,m,k;
int res;
struct node
{
    int x,y;
}a[N];
struct edg
{
    int p,l,h;
}b[N];
signed main()
{
 
   cin>>n>>m>>k;
   for(int i=0;i<=n;i++) 
       for(int j=0;j<=m;j++)
           f[i][j]=0x3f3f3f3f;
   for(int i=1;i<=n;i++)
   {
       b[i].l=0;
       b[i].h=1001;
   }
   for(int i=1;i<=n;i++)
   {
        cin>>a[i].x>>a[i].y;
   }
   for(int i=1;i<=k;i++)  
   {
        int xx;
        cin>>xx;
        st[xx]=1;
        cin>>b[xx].l>>b[xx].h;
   }
   for(int j=0;j<=1000;j++) f[0][j]=0;
   for(int i=1;i<=n;i++)
   {
       for(int j=a[i].x;j<=a[i].x+m;j++)
       {
           f[i][j]=min(f[i-1][j-a[i].x]+1,f[i][j-a[i].x]+1);
       }
       for(int j=m+1;j<=a[i].x+m;j++)
       {
           f[i][m]=min(f[i][m],f[i][j]);
       }
       for(int j=1;j<=m-a[i].y;j++)
       {
           f[i][j]=min(f[i][j],f[i-1][j+a[i].y]);
       }
       for(int z=0;z<=b[i].l;z++)    f[i][z]=0x3f3f3f3f;
       for(int z=b[i].h;z<=m;z++)    f[i][z]=0x3f3f3f3f;
   }
   int ans=0x3f3f3f3f;
   for(int i=1;i<=m;i++)    ans=min(ans,f[n][i]);
   if(ans<0x3f3f3f3f)    cout<<1<<endl<<ans<<endl;
   else  
   {
       int flag=0;
       ans=0;
       for(int i=n;i>=1;i--)
       {
           for(int j=1;j<=m;j++)
           {
               if(f[i][j]<0x3f3f3f3f) 
               {
                   flag=1;
                   break;
               }
           }
           if(!flag) ans+=st[i];
           else break;
       }
       cout<<0<<endl<<k-ans<<endl;
   }
}

ST倍增

最开始得知这个名词还是这个题：
1273. 天才的记忆
1273链接
题意：给定一个序列，查询某个区间的最大值。
思路：
$f [i] [j]$ 表示从 $i$ 开始，长度是 $2^j$ 的区间中的最值。
$f[i][j]=max(f[i][j-1],f[i+2^{j-1},j-1])$ 。
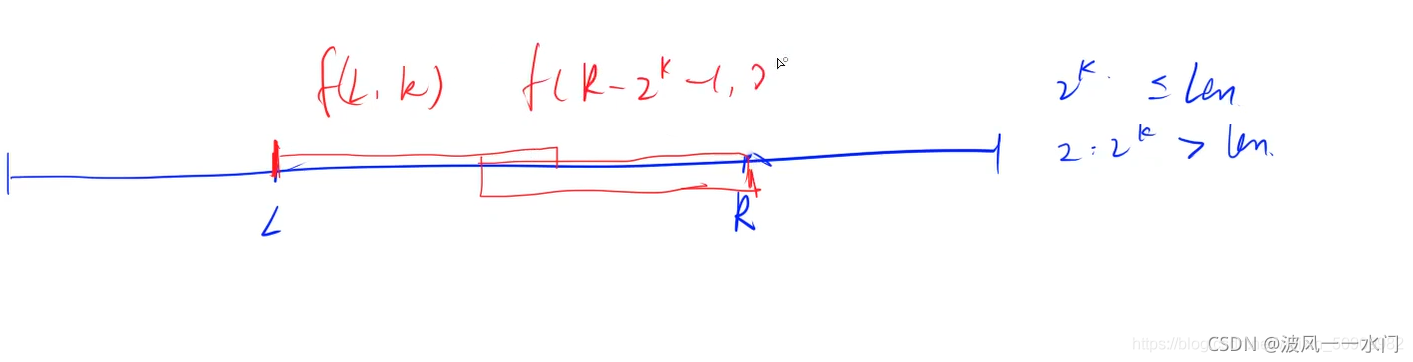
在这里插入图片描述

找到一个 $k$ 使得 $2^k<=len$ 的最大的 $k$ ，那么 $2·2^{k}>len$ ，所以枚举 $l,k)和(r-2^k-1,r)$ 就可以取得这个区间所有的最值情况。
那么如何快速找到使得 $2^k<=len$ 的最大的 $k$ 呢：
$k=[log_2{len}]向下取整$
$k=[\frac{log_{10}len}{log_{10} 2}]向下取整$
这一步可以使用log函数——返回以10为底的 $l o g$ 数。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 200010, M = 18;

int n, m;
int w[N];
int f[N][M];

void init()
{
    for (int j = 0; j < M; j ++ )//类似区间 DP ，先循环长度
        for (int i = 1; i + (1 << j) - 1 <= n; i ++ ) // (1<<j-1)是区间长度，加上区间长度要小于 n 
            if (!j) f[i][j] = w[i];// j = 0 代表就一个数
            else f[i][j] = max(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
}

int query(int l, int r)
{
    int len = r - l + 1;
    int k = log(len) / log(2);

    return max(f[l][k], f[r - (1 << k) + 1][k]);
}

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);

    init();

    scanf("%d", &m);
    while (m -- )
    {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", query(l, r));
    }

    return 0;
}

P1613 跑路
P1613链接
题意：A 从 1 跑到 n ，有一个空间跑路器可以让他每秒跑 $2^k$ 千米，让你求从 1 到 n 的最短时间。
思路：这道题不能直接跑最短路，因为跑路器会合并一些路径，形成更短的时间，所以我们预处理出来在跑路器意义下的最短路径，最后更新一遍时间作为答案。
在预处理的时候，还是用倍增的思想
$vis[i][j][k]表示从i到j的路径长度为2^k$
$然后n^3枚举点对即可，最外边循环k。$
先枚举k是为了在转移当前状态时，保证他前面所有的 $2^{1...k-1}$ 的状态表示的路径已经是最优的了。

#include<bits/stdc++.h>
using namespace std;
const int N=70;
bool vis[N][N][N];
int dist[N][N];
int main()
{   
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if(i==j)  dist[i][j]=0;
            else dist[i][j]=0x3f3f3f3f;
        }
    }
    while(m--)
    {
        int a,b;
        cin>>a>>b;
        dist[a][b]=1;
        vis[a][b][0]=true;
    }
    for(int k=1;k<=64;k++)
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            for(int t=1;t<=n;t++)
            {
                if(vis[i][j][k-1]&&vis[j][t][k-1])
                {
                    dist[i][t]=1;
                    vis[i][t][k]=true;
                }
            }
        }
    }
    for(int k=1;k<=n;k++)
    {
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            {
                dist[i][j]=min(dist[i][j],dist[i][k]+dist[k][j]);
            }
        }
    }
    cout<<dist[1][n]<<endl;
}

区间DP

P4170 [CQOI2007]涂色
在这里插入图片描述
思路：这道题显然是区间DP，然后从样例分析，我最开始想到的状态转移时当 $f [i] [j]$ 所代表的这个区间的染色的两个端点 i 和 j 相等时, $f [i + 1] [j - 1]$ 可以多染出两边的格子。但其实再分析的话， $f [i + 1] [j]$ 也可以多染 i 这个格子， $f [i] [j - 1]$ 也可以多染 j 这个格子，所以 $f [i] [j]$ 可以由这三个状态转移过来，但是如果考虑后两种状态的话，第一种状态就是他们的子状态，不需要再考虑了。其他的就是区间DP板子。

#include<bits/stdc++.h>
#include<cstring>
using namespace std;
int dp[55][55];
char st[55];
int main()
{   
    cin>>st+1;
    int n=strlen(st+1);
    memset(dp,0x3f,sizeof dp);
    for(int i=1;i<=n;i++)
    {
        dp[i][i]=1;
    }
    for(int len=2;len<=n;len++)
    {
        for(int i=1;i+len-1<=n;i++)
        {
            int j=i+len-1;
            if(st[i]==st[j])
            {
                dp[i][j]=min(dp[i][j-1],dp[i+1][j]);
            }
            for(int k=i;k<j;k++)
            {
                dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]);
            }
        }
    }
    cout<<dp[1][n]<<endl;
}

关路灯
总感觉这个题挺难的，没想明白以后再说~555

#include <bits/stdc++.h>

const int N = 55;

int f[N][N][2] , n , c;
int pos[N] , w[N] , sum[N];

int _min(int a , int b) {
	return a < b ? a : b;
}

int main () {
	scanf("%d %d" , &n , &c);
	for(int i = 1 ; i <= n ; ++ i) scanf("%d %d" , pos + i , w + i) , sum[i] = sum[i - 1] + w[i];
	for(int i = 1 ; i <= n ; ++ i)
		for(int j = 1 ; j <= n ; ++ j) f[i][j][1] = f[i][j][0] = 1000000000; 
	f[c][c][0] = f[c][c][1] = 0;
	for(int len = 2 ; len <= n ; ++ len) {
		for(int i = 1 ; i <= n - len + 1 ; ++ i) {
			int j = i + len - 1;
			f[i][j][1] = _min(f[i + 1][j][1] + (pos[i + 1] - pos[i]) * (sum[n] - sum[j] + sum[i]) , f[i + 1][j][0] + (pos[j] - pos[i]) * (sum[n] - sum[j] + sum[i]));
			f[i][j][0] = _min(f[i][j - 1][0] + (pos[j] - pos[j - 1]) * (sum[i-1] + sum[n] - sum[j-1]) , f[i][j - 1][1] + (pos[j] - pos[i]) * (sum[i-1] + sum[n] - sum[j-1]));
		}
	}
	printf("%d" ,_min(f[1][n][1] , f[1][n][0]));
	return 0;
}

P4342 [IOI1998]Polygon
在这里插入图片描述
题意：就是一个环，每个点有权值，每个边要么是 + 号连接，要么是 * 号连接，让你断开一条边，求剩下的链按边上的符号合并的最大值。
思路：这道题的区间合并的加法很显然：直接相加

但是思考一下这个乘法可以直接相乘吗？
我们看图片也可以看见点权有负数，所以最小值乘最小值也可能是最大值，不一定是当前的最大值乘最大值。
所以如上所述我们维护最大值和最小值的话：这两种情况都可能取得最大值。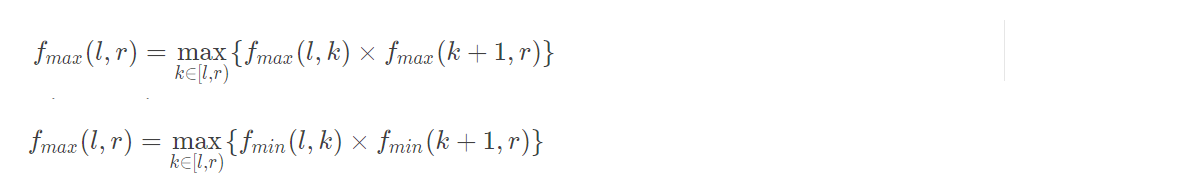在这里插入图片描述
同理这两种情况也可以维护最小值：

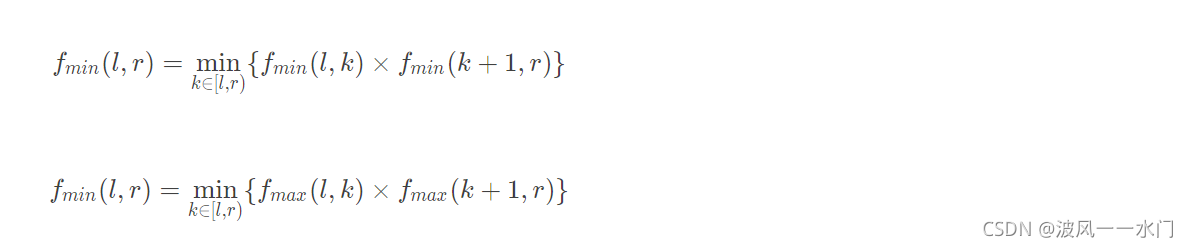
此时还漏下了一种情况，就是一大一小如果得到的值不是最大值，反而是个很小的负数，但是这个数一旦碰到负数就可能转化成最大值，所以一正一负的情况也得被更新出来。
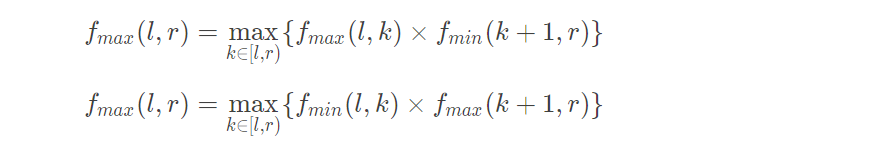
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
const int N = 115;
int f[N][N] , n , a[N] , g[N][N];
char w[N];
signed main()
{
	cin >> n;
	for(int i = 1 ; i <= n ; i ++)
	{
		cin >> w[i] >> a[i];
		w[i + n] = w[i];
		a[i + n] = a[i];
	}
	for(int len = 1 ; len <= n ; len ++)
	{
		for(int l = 1 ; l + len - 1 <= 2 * n ; l ++)
		{
			int r = l + len - 1;
			if(len == 1)
			{
				f[l][r] = g[l][r] = a[l];
			}
			else
			{
				f[l][r] = -0x3f3f3f3f;
				g[l][r] = 0x3f3f3f3f;
				for(int k = l ; k < r ; k ++)
				{
					int x1 = f[l][k] * f[k + 1][r] , x2 = f[l][k] * g[k + 1][r] , x3 = g[l][k] * f[k + 1][r] , x4 = g[l][k] * g[k + 1][r]; 
					if(w[k + 1] == 't')
					{
						f[l][r] = max(f[l][r] , f[l][k] + f[k + 1][r]);
						g[l][r] = min(g[l][r] , g[l][k] + g[k + 1][r]);
					}
					else
					{
						f[l][r] = max({f[l][r] , x1 , x2 , x3 , x4});
						g[l][r] = min({g[l][r] , x1 , x2 , x3 , x4});
					}
				}
			}
		}
	}
	int res = 0;
	for(int i = 1 ; i <= 2 * n ; i ++)
	{
		res = max(res , f[i][i + n - 1]);
	}
	cout << res << endl;
	for(int i = 1; i <= n ; i ++)
	{
		if(f[i][i + n - 1] == res)  cout << i << ' ';
	}
}

CF1114D Flood Fill
给定一个串，让你选定一个下标，每次操作这个下标所在的那个连通块的颜色，如果某个连通块的颜色相同就可以改变，问你所有连通块同色的最小步骤。
在这里插入图片描述

就比如这个样例，如果我们选定某个下标为3的颜色“5”，我们就不能改变“1” 和 “4” 的颜色为 5 。我一开始模拟这个样例老觉得答案是3，结果是题意理解错了。
这个题我们可以先把连续的同色缩成一个点，这样对答案没有影响。
我们可以发现一个性质：选定一个下标改变颜色，那对于一个子序列 {x , y ,z}来说，我们选定 y 作为下标，最后这个子序列的颜色一定是 x 或者是 z 。
如果x 和 y 同色，那么就是 y 这个子区间的答案 +1。
如果x 和 y 不同色，那么答案可以是 min(x 和 y 同色之后的答案, y 和 z 同色之后的答案) + 1 ，当然你也可以说 y 这个子区间的答案 + 2，但是仔细一想就发现这是个子状态了，不需要考虑。
所以最后 $f [i] [j]$ 的答案只需要讨论区间端点，而不用枚举区间中的每一个断点，所以想到这里我们就能明白为什么题目给出这样一个数据范围了。
$1≤n,c_i ≤5000。$
根据上述讨论很容易写出转移方程:
$端点相同： f [l] [r] = f [l + 1] [r - 1] + 1$
$端点不同： f [l] [r] = min (f [l + 1] [r], f [l] [r - 1]) + 1;$

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5010;
int f[N][N];
int a[N];
signed main()
{
    int n;
    cin>>n;
    int ct=0;
    int cnt=1;
    for(int i=1;i<=n;i++)  
    {
        int x; cin>>x;
        if(x!=a[cnt-1])
        {
            a[cnt++]=x;
        }
    }
    for(int  len=2;len<=cnt-1;len++)
    {
        for(int i=1;i+len-1<=cnt-1;i++)
        {
            int l=i,r=i+len-1;
            if(a[l]==a[r])
            {
                f[l][r]=f[l+1][r-1]+1;
            }
            else f[l][r]=min(f[l+1][r],f[l][r-1])+1;
        }
    }
    cout<<f[1][cnt-1]<<endl;
}

P3146 [USACO16OPEN]248 G
P3146
给定一个1*n的地图，在里面玩2048，每次可以合并相邻两个（数值范围1-40），问序列中出现的最大数字的值最大是多少。注意合并后的数值并非加倍而是+1，例如2与2合并后的数值为3。

#include<bits/stdc++.h>
using namespace std;
const int N = 300;
int f[N][N];
int a[N],ans;
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) f[i][i]=a[i];
    for(int len=2;len<=n;len++)
    {
        for(int i=1;i+len-1<=n;i++)
        {
            int j=i+len-1;
            for(int k=i;k<j;k++)
            {
                if(f[i][k]==f[k+1][j])
                {
                    f[i][j]=max(f[i][j],f[i][k]+1);
                }
            }
            ans=max(ans,f[i][j]);
            //cout<<" i = "<<i<<" j = "<<j<<" f[i][j] = "<<f[i][j]<<endl;
        }
    }
   cout<<ans<<endl;
}

波风一一水门

关注

4
点赞
踩
4

收藏

觉得还不错? 一键收藏
0
评论
DP小题单【2】

题目列表见：DP小题单【1】单调队列维护窗口最值acwing模板题最大子序和#include<bits/stdc++.h>using namespace std;typedef long long LL;int n,m;const int N=3e5+10;int a[N];int q[N];int main(){ cin>>n>>m; for(int i=1;i<=n;i++) { cin>&
复制链接

扫一扫