同余问题详解

同余问题学习笔记

1.同余符号

若任意两个整数 $a,b$ 模 $m$ 的值是相同的，那么我们可以表示成以下形式
$$a\equiv b(\mathrm{mod}m)$$
读作： $a$ 同余于 $b$ 模 $m$ ，或读作 $a$ 与 $b$ 对模 $m$ 同余

2.同余符号的性质

1.反身性：$a\equiv a(\mathrm{mod}m)$；

证明：$a$ 模 $m$ 一定等于 $a$ 模 $m$

2.对称性：若$a\equiv b(\mathrm{mod}m)$，则$b\equiv a(\mathrm{mod}m)$；

证明：$a$ 与 $b$ 同余，$b$ 一定和 $a$ 同余。

3.传递性：若$a\equiv b(\mathrm{mod}m)$，$b\equiv c(\mathrm{mod}m)$，则$a\equiv c(\mathrm{mod}m)$；

证明：设 $a,b,c$ 对 $m$ 取余分别为 $x,y,z$ ，那么 $x=y,y=z,x=z$。

4.同余式相加：若$a\equiv b(\mathrm{mod}m)$，$c\equiv d(\mathrm{mod}m)$，则 ,$a\pm c\equiv b\pm d(\mathrm{mod}m)$

5.同余式相乘：若$a\equiv b(\mathrm{mod}m)$，$c\equiv d(\mathrm{mod}m)$，则$ac\equiv bd(\mathrm{mod}m)$。

然后当 $a,b$ 模 $m$ 同余的时候，那么 $m|(a-b)$

那么我们 $a$ 看成 $km+r$ ，这里 $k$ 为 $a/m$ 的商，$r$ 为 $a\mathrm{mod}m$ ，同理，我们将 $b$ 看成 $lm+r$

那么我们将 $m$ 提出来，两数相减即为 $(k-l)m$ 所以 $a-b$ 即为 $m$ 的倍数。

3.相关定理

1.裴蜀定理

若 $a,b$ 是整数,且 $\gcd (a,b)=d$，那么对于任意的整数 $x,y,ax+by$ 都一定是 $d$ 的倍数
特别地，一定存在整数 $x,y$，使 $ax+by=d$ 成立

证明：

既然是求 $\gcd$ ，我们就可以模拟一下欧几里得算法(可以先看后面)

我们设 $a\le b$ ,由辗转相除法的过程 $\gcd (x,y)=\gcd (y,x\mathrm{mod}y)$,可以得到

$b=a{x}_1+r_1$，那么 $b\mathrm{mod}a$ 后 $b=r_1$

重复过程，得到以下式子：
$$\begin{gathered} b=a{x}_1+r_1 \\ a=a{x}_2+r_2 \\ {r}_1=r_2{x}_3+r_3 \\ ...... \\ {r}_{k-3}=r_{k-2}{x}_{k-1}+r_{k-1}(1) \\ {r}_{k-2}=r_{k-1}{x}_k+r_k(2) \\ {r}_{k-1}=r_k{x}_{k+1}+r_{k+1} \end{gathered}$$
因为辗转相除法最后得到的余数为 $0$，在这里，我们不妨设 $r_{k+1}=0$ ,那么，$r_k$ 就是 $a,b$ 的最大公约数，即 $r_k=d$ ，将这个东西带入 $(2)$ 式子，那么这个时候我们得到以下式子
$$r_{k-2}=r_{k-1}{x}_k+d$$
移项得到
$$d=r_{k-2}-r_{k-1}{x}_k(3)$$
将 $(1)$ 式子移项
$$r_{k-1}=r_{k-3}-r_{k-2}{x}_k(4)$$
$(4)$ 式带入 $(3)$

$d=r_{k-2}-(r_{k-3}-r_{k-2}{x}_k)x_k$

把式子展开

$d=m_1{r}_{k-2}+n_1{r}_{k-3}$

很明显，我们上面用的都是整数，所以 $m_1,n_1$ 肯定也都是整数，那如果我们把原来的 $(3)$ 式子转化成这种形式 $d=m{r}_{k-1}+n{r}_{k-2}$。

我们将这个式子跟上面的一对比，是不是发现了什么规律？

$d=m_{k}a+n_{k}b$

我们知道，$m_k$ 和 $n_k$ 都是整数，故 $ax+by=d$ 一定有整数解。

---

推论1：对于方程 $ax+by=1$ , 只有当整数 $a,b$ 互质时，方程才有整数解.

反证法：

这 $a,b$ 不是互质的，那么 $a,b$ 可以表示成 $a=q\ast \gcd (a,b)$ ， $b=p\ast \gcd (a,b)$， 带入上面的式子，易得
$$q\ast \gcd (a,b)\ast x+p\ast \gcd (a,b)\ast y=1$$
如果两边同时除以一个 $\gcd (a,b)$,得到：
$$qx+py=\frac{1}{\gcd (a,b)}$$
显然，如果 $a,b$ 不是互质的话，那么等式右边就是一个小数，所以该方程不存在整数解，得证。

另外，可以得到 $a,b$ 互质的充要条件就是 $ax+by=1$ 要有整数解

---

推论2: 对于方程 $ax+by=z$ , 只有满足 $\gcd (a,b)|z$ ，方程才有整数解

证明：

设 $d=\gcd (a,b)$ ，$z=d\ast q$

对于方程 $ax+by=d$ ，我们有一组解 $x_1,y_1$,那么就有：
$$a{x}_1+b{y}_1=d$$
两边同时乘上 $q$ ,易得：
$$a{x}_1\ast q+b{y}_1\ast q=d\ast q$$
因为 $z=d\ast q$

所以方程 $ax+by=z$ ，一定存在一组整数解 $x=x_1\ast q,y=y_1\ast q$,得证。

2.欧几里得算法

欧几里得算法的目的是简单的求出两个正整数的最大公因数。

那么我们证明一下这个算法：

令 $c=\gcd (a,b)$，设$a=mc，b=nc$；
由$a÷b=k......r$可得 $r=a-kb=mc-knc=(m-kn)c$；
第二步不难看出，$c$ 也是 $r$ 的因数；
列出 $b=nc$ 和 $r=(m-kn)c$ ，如果 $n$ 和 $m-kn$ 互质，即两者公约数只有 $1$ ，则表明 $c$ 是 $b$ 和 $r$ 的最大公约数，后续证明 $n$ 和 $m-kn$ 互质；
假设 $m-kn$ 和 $n$ 不是互质，两者有一非零的最大公约数 $d$ ，且 $d＞1$ ；
则有 $m-kn=xd $，$n=yd$，得 $m=kn+xd=kyd+xd=(ky+x)d$ ，则 $a=mc=(ky+x)dc$ ，$b=nc=ycd$，则 $a$ 与 $b$ 的一个公约数 $cd＞c$，故 $c$ 不是 $a$ 与 $b$ 的最大公约数，这与前面提到的 $c$ 是 $a$ 与$b$ 的最大公约数假设矛盾；
故 $m-kn$ 和 $n$ 为互质，即 $c$ 是 $b$ 和 $r$ 的最大公约数，且是 $a$ 和 $b$ 的最大公约数，得证。

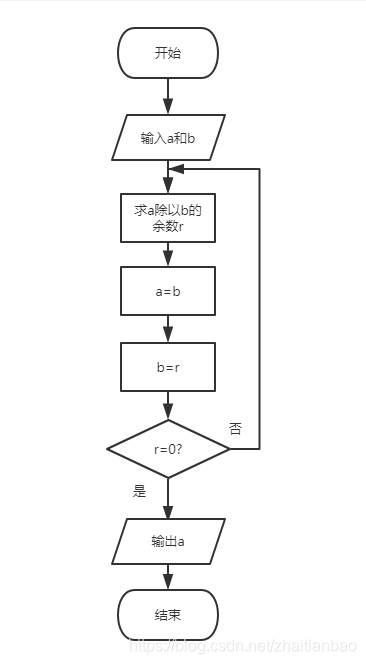
此算法实现流程图：

](https://imgtu.com/i/vK4hkD)

3.扩展欧几里得算法

对于求解方程 $ax+by=\gcd (a,b)$

先考虑特殊情况，如果 $b=0$ ，那么 $\gcd (a,b)=a$，显然存在一组解 $x=1,y=0$

设之前的方程为 $a{x}_1+b{y}_1=\gcd (a,b)$ ，肯定存在式子 $b{x}_2+(a\mathrm{mod}b)y_2=\gcd (b,a\mathrm{mod}b)$

根据刚刚讲的欧几里得算法，$\gcd (a,b)=\gcd (b,a\mathrm{mod}b)$

所以 $a{x}_1+b{y}_1=b{x}_2+(a\mathrm{mod}b)$

因为 $a\mathrm{mod}b=a-a/b\ast b$

所以 $a{x}_1+b{y}_1=b{x}_2+(a-a/b\ast b)\ast y_2$

​ $a{x}_1+b{y}_1=b{x}_2+a-a/b\ast b\ast y_2$

​ $a{x}_1+b{y}_1=a{y}_2+b(x_2-a/b\ast y_2)$

所以 $x_1=y_2,y_1=x_2-a/b\ast y_2$

code:

void exgcd(ll a, ll b)
{
    if(b == 0)
    {
        x = 1, y = 0;
        return;
    }
    exgcd(b, a % b);
    ll t = x;
    x = y;
    y = t - a / b * y;
}

然后我们这个东西还能求逆元，怎么求呢？

设 $x$ 为 $a$ 模 $p$ 意义下的逆元，那么满足式子：

$ax\equiv 1(\mathrm{mod}m)$

那么有 $ax+my=1$， 接着用扩展欧几里得定理来做即可。

更加详细的理解
更加详细的理解