LeetCode 图-岛屿问题

最新推荐文章于 2025-11-04 19:09:55 发布

原创

最新推荐文章于 2025-11-04 19:09:55 发布 · 1.3k 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #职场和发展

图

图的基本知识
LeetCode 相关题目
- 岛屿问题
- - 岛屿的最大面积
  - 岛屿的周长

图的基本知识

基本概念

图的类型

无向图
有向图
加权图

图的存储

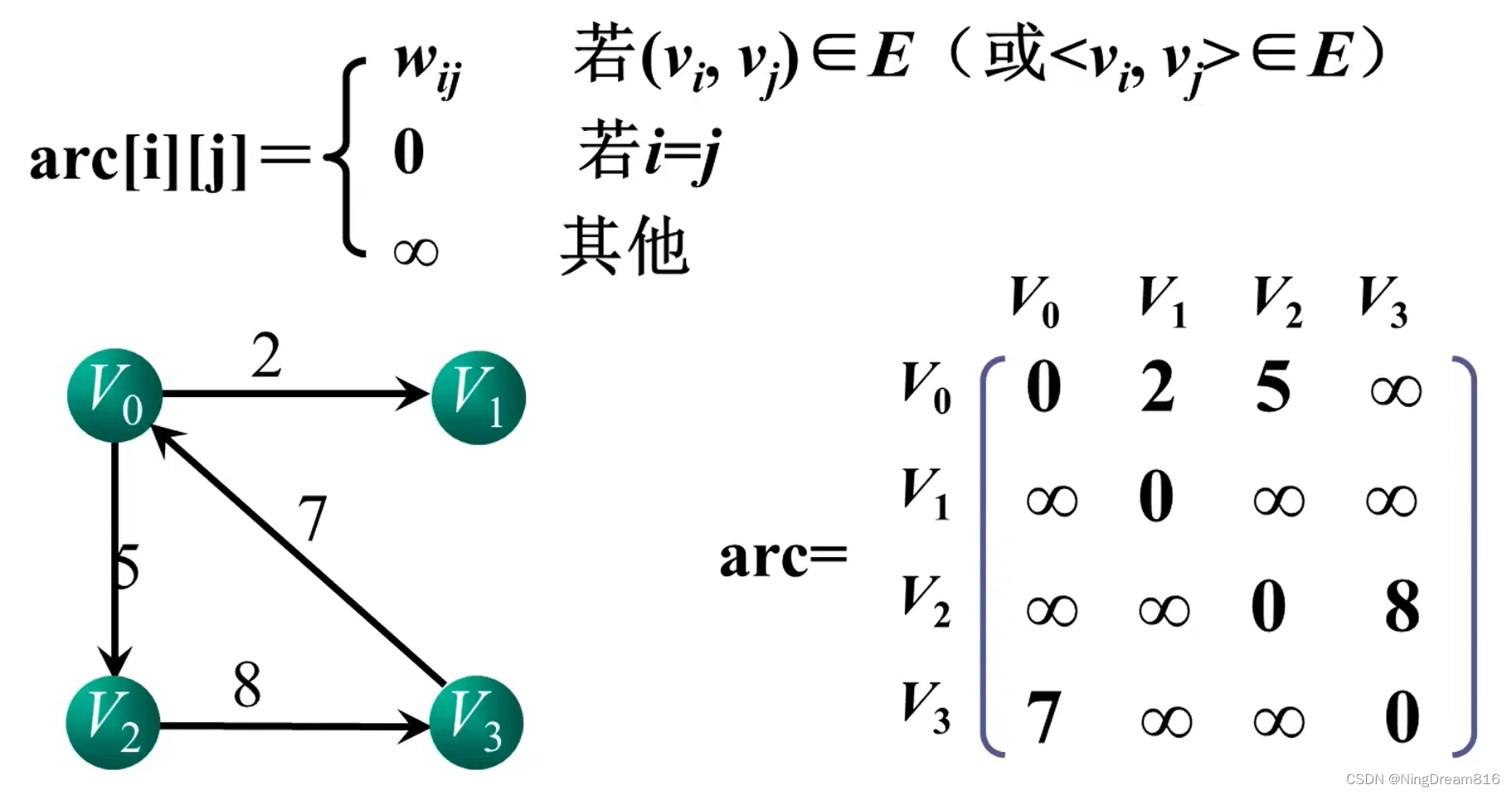
邻接矩阵存储：是用一个二维数据数组(矩阵)存储图中顶点间的邻接关系。假设图G=(V, E)有n个顶点，那么邻接矩阵就是n*n的方阵。

以有权图为例：
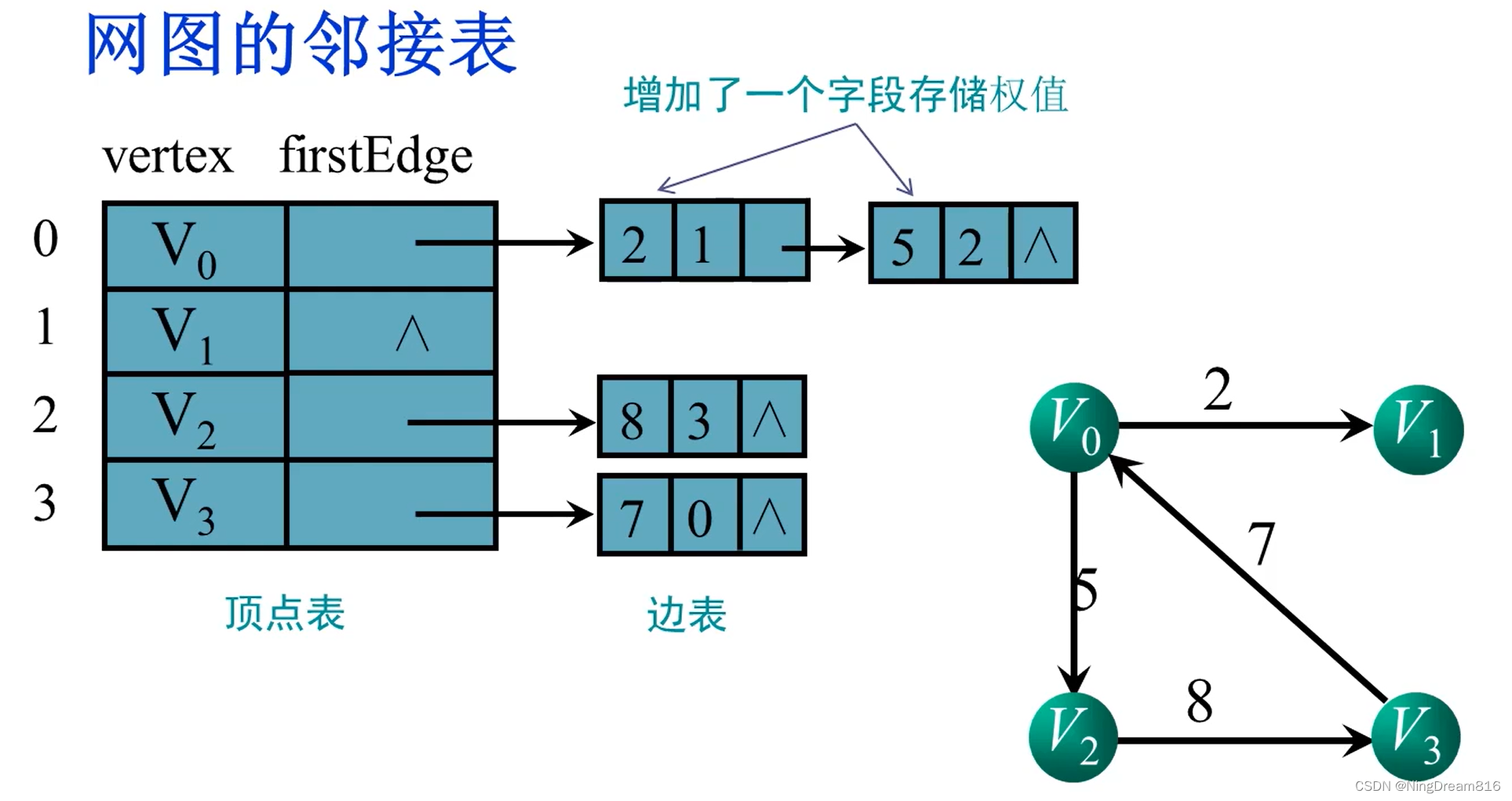
在这里插入图片描述

邻接表：对于每个图的顶点v，将所有邻接于顶点v的顶点链成一个单链表（边表）。
以有权图为例：

LeetCode 相关题目

岛屿问题

我们所熟悉的 DFS（深度优先搜索）问题通常是在树或者图结构上进行的。而今天讨论的 DFS 问题，是在一种「网格」结构中进行的。岛屿问题是这类网格 DFS 问题的典型代表。

网格类问题的 DFS 遍历方法：

网格问题是由 m * n 个小方格组成一个网格，每个小方格与其上下左右四个方格认为是相邻的，要在这样的网格上进行某种搜索。
岛屿问题每个格子中的数字可能是 0 或者 1。0 看成海洋，1 看成陆地，这样相邻的陆地就连接成一个岛屿。在这样一个设定下，就出现了各种岛屿问题的变种，包括岛屿的数量、面积、周长等。

二叉树 DFS 遍历一般是这样的：

void dfs(TreeNode* root) {
   
   
	// base case
	if (root == nullptr) return;
	// visit adjacent node
	dfs(root->left);
	dfs(root->right);
}

其中最关键的是处理好base case 的判断，以及访问相邻节点。在网格问题中，相邻节点就是上下左右四个格子，base case 就是数组下标越界的情况。
于是可以写出网格问题 dfs 遍历的代码：

void dfs(vector<vector<int>>& grid, int r, int c) {
   
   
	// base case
	if (!inArea(grid, r, c) return;
	
	// visit adjacent
	dfs(grid, r - 1, c);
	dfs(grid, r + 1, c);
	dfs(grid, r, c - 1);
	dfs(grid, r, c + 1);
}

bool inArea(vector<vector<int>>& grid, int r, int c) {
   
   
	return r >= 0 && r < grid.size() && c >= 0 &&<