关于卷积神经网络中一些名词的解释合集（Feature map,filter,上下采样等）

feather map的理解 在cnn的每个卷积层，数据都是以三维形式存在的。你可以把它看成许多个二维图片叠在一起（像豆腐皮一样），其中每一个称为一个feature map。

feather map 是怎么生成的？ 输入层：在输入层，如果是灰度图片，那就只有一个feature map；如果是彩色图片，一般就是3个feature map（红绿蓝）。

其它层：层与层之间会有若干个卷积核（kernel）（也称为过滤器），上一层每个feature map跟每个卷积核做卷积，都会产生下一层的一个feature map，有N个卷积核，下层就会产生N个feather map。

多个feather map的作用是什么？ 在卷积神经网络中，我们希望用一个网络模拟视觉通路的特性，分层的概念是自底向上构造简单到复杂的神经元。楼主关心的是同一层，那就说说同一层。 我们希望构造一组基，这组基能够形成对于一个事物完备的描述，例如描述一个人时我们通过描述身高/体重/相貌等，在卷积网中也是如此。在同一层，我们希望得到对于一张图片多种角度的描述，具体来讲就是用多种不同的卷积核对图像进行卷，得到不同核（这里的核可以理解为描述）上的响应，作为图像的特征。他们的联系在于形成图像在同一层次不同基上的描述。

下层的核主要是一些简单的边缘检测器（也可以理解为生理学上的simple cell）。

上层的核主要是一些简单核的叠加（或者用其他词更贴切），可以理解为complex cell。

多少个Feature Map？真的不好说，简单问题少，复杂问题多，但是自底向上一般是核的数量在逐渐变多（当然也有例外，如Alexnet），主要靠经验。

卷积核的理解 卷积核在有的文档里也称为过滤器（filter）：

每个卷积核具有长宽深三个维度； 在某个卷积层中，可以有多个卷积核：下一层需要多少个feather map，本层就需要多少个卷积核。 卷积核的形状 每个卷积核具有长、宽、深三个维度。在CNN的一个卷积层中：

卷积核的长、宽都是人为指定的，长X宽也被称为卷积核的尺寸，常用的尺寸为3X3，5X5等； 卷积核的深度与当前图像的深度（feather map的张数）相同，所以指定卷积核时，只需指定其长和宽 两个参数。例如，在原始图像层 （输入层），如果图像是灰度图像，其feather map数量为1，则卷积核的深度也就是1；如果图像是grb图像，其feather map数量为3，则卷积核的深度也就是3.

卷积核个数的理解 如下图红线所示：该层卷积核的个数，有多少个卷积核，经过卷积就会产生多少个feature map，也就是下图中 豆腐皮儿的层数、同时也是下图豆腐块的深度（宽度）！！这个宽度可以手动指定，一般网络越深的地方这个值越大，因为随着网络的加深，feature map的长宽尺寸缩小，本卷积层的每个map提取的特征越具有代表性（精华部分），所以后一层卷积层需要增加feature map的数量，才能更充分的提取出前一层的特征，一般是成倍增加（不过具体论文会根据实验情况具体设置）！

多通道卷积，但卷积核只有一个

多通道卷积，卷积核数量多个

 

filter的理解 filter有两种理解：

在有的文档中，一个filter等同于一个卷积核：只是指定了卷积核的长宽深；

而有的情况（例如tensorflow等框架中，filter参数通常指定了卷积核的长、宽、深、个数四个参数），filter包含了卷积核形状和卷积核数量的概念：即filter既指定了卷积核的长宽深，也指定了卷积核的数量。

参考链接：https://blog.csdn.net/xys430381_1/article/details/82529397

filter大小一般是奇数。

padding

默认stride=1

same convolution:当使用padding时，新产生的结果的大小：

valid convolution:当没有使用的时候是：(n-f+1)(n-f+1)

步幅stride

当使用padding(p),设置stride时，结果：(n+2p-f)/s+1 向下取整

三维卷积的结果：（结合上面的filter理解应该能看懂）

1×1卷积

 

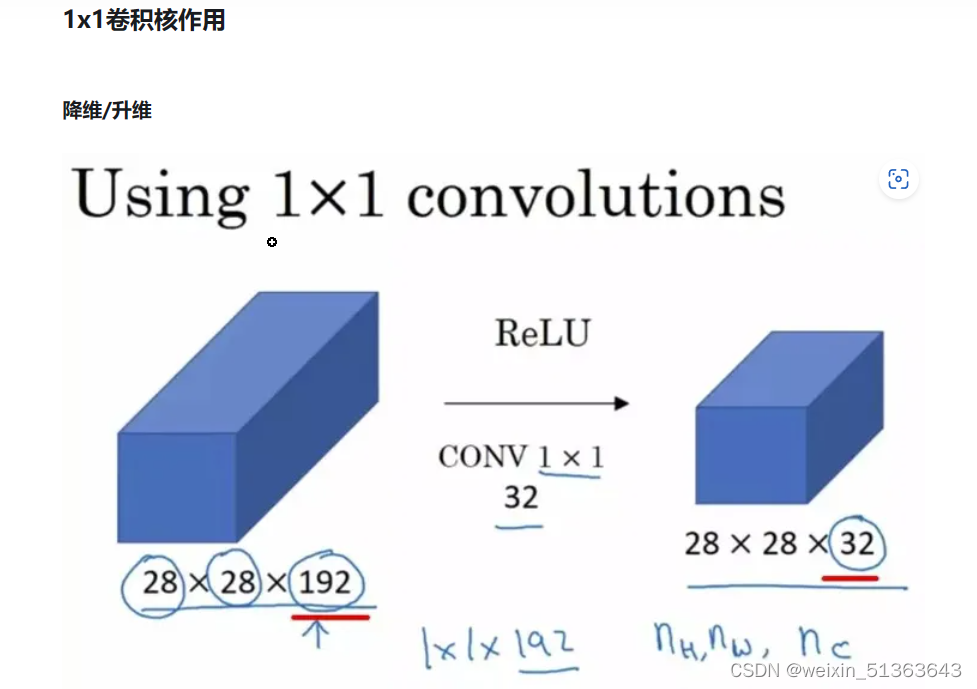
same卷积是有损降维，1×1卷积是无损降维

在Inception和ResNet中都有应用。

一文读懂卷积神经网络中的1x1卷积核 - 知乎 (zhihu.com)

Pooling

一般没有padding, 池化会减小高和宽（降维），但channel不会改变。

它实际上是一种形式的降采样。有多种不同形式的非线性池化函数，而其中“最大池化（Max pooling）”是最为常见的。它是将输入的图像划分为若干个矩形区域，对每个子区域输出最大值。直觉上，这种机制能够有效地原因在于，在发现一个特征之后，它的精确位置远不及它和其他特征的相对位置的关系重要。池化层会不断地减小数据的空间大小，因此参数的数量和计算量也会下降，这在一定程度上也控制了过拟合。通常来说，CNN的卷积层之间都会周期性地插入池化层。

池化的作用： 池化操作后的结果相比其输入缩小了。池化层的引入是仿照人的视觉系统对视觉输入对象进行降维和抽象。在卷积神经网络过去的工作中，研究者普遍认为池化层有如下三个功效：

　　1.特征不变性：池化操作是模型更加关注是否存在某些特征而不是特征具体的位置。其中不变形性包括，平移不变性、旋转不变性和尺度不变性。

平移不变性是指输出结果对输入对小量平移基本保持不变，例如，输入为(1, 5, 3), 最大池化将会取5，如果将输入右移一位得到(0, 1, 5)，输出的结果仍将为5。对伸缩的不变形，如果原先的神经元在最大池化操作后输出5，那么经过伸缩（尺度变换）后，最大池化操作在该神经元上很大概率的输出仍是5.

　　2.特征降维（下采样）：池化相当于在空间范围内做了维度约减，从而使模型可以抽取更加广范围的特征。同时减小了下一层的输入大小，进而减少计算量和参数个数。

　　3.在一定程度上防止过拟合，更方便优化。

    4.实现非线性（类似relu）。

    5.扩大感受野。

代码：

torch.nn.functional.avg_pool2d(input, kernel_size, stride=None, 
  padding=0, ceil_mode=False, count_include_pad=True)

下采样和上采样

缩小图像（或称为下采样（subsampled）或降采样（downsampled））的主要目的有两个：

1、使得图像符合显示区域的大小；

2、生成对应图像的缩略图。

放大图像（或称为上采样（upsampling）或图像插值（interpolating））的主要目的是：放大原图像,从而可以显示在更高分辨率的显示设备上。

上采样和下采样都是一种抽象描述，其具体实现有很多种方式：

下采样：

1. 用stride为2的卷积层实现：卷积过程导致的图像变小是为了提取特征。下采样的过程是一个信息损失的过程，而池化层是不可学习的，用stride为2的可学习卷积层来代替pooling可以得到更好的效果，当然同时也增加了一定的计算量。

2. 用stride为2的池化层实现：池化下采样是为了降低特征的维度。如Max-pooling和Average-pooling，目前通常使用Max-pooling，因为他计算简单而且能够更好的保留纹理特征。

上采样：

1. 插值，一般使用的是双线性插值，因为效果最好，虽然计算上比其他插值方式复杂，但是相对于卷积计算可以说不值一提，其他插值方式还有最近邻插值、三线性插值等；

2. 转置卷积又或是说反卷积(Transpose Conv)，通过对输入feature map间隔填充0，再进行标准的卷积计算，可以使得输出feature map的尺寸比输入更大；相比上池化，使用反卷积进行图像的“上采样”是可以被学习的（会用到卷积操作，其参数是可学习的）。

   1.Up-Pooling - Max Unpooling && Avg Unpooling --Max Unpooling，在对称的max pooling位置记录最大值的索引位置，然后在unpooling阶段时将对应的值放置到原先最大值位置，其余位置补0；

   （相当于是max pooling的反向传播）

 2.PixelShuffle（像素重组）

下面评论有一个点：