Leetcode刷题记录27——除自身以外数组的乘积

题源：https://leetcode.cn/problems/product-of-array-except-self/description/?envType=study-plan-v2&envId=top-100-liked

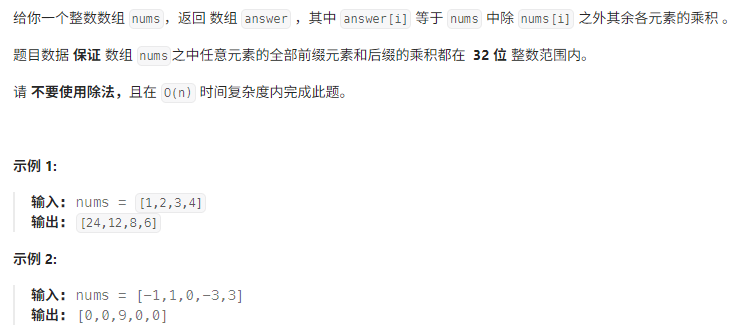
题目描述：

思路一：
我们可以通过两个辅助数组来分别记录：

• **前缀乘积：**当前位置左边所有数的乘积。
• **后缀乘积：**当前位置右边所有数的乘积。

最后将这每个数的前缀乘积和后缀乘积相乘，即可得到最终结果。

具体实现步骤：

第一步：初始化前后缀数组

pre_product = [1] * len(nums)
suf_product = [1] * len(nums)

pre_product[i] 表示从 nums[0] 到 nums[i-1] 的乘积。
suf_product[i] 表示从 nums[i+1] 到 nums[-1] 的乘积。

初始值都为 1，表示没有前面或后面元素时的乘积为 1。

第二步：构造前缀乘积数组

for i in range(1, len(nums)):
    pre_product[i] = pre_product[i - 1] * nums[i - 1]

从前向后遍历，每一步都在前一个前缀的基础上乘上当前的数字。例如：

nums = [1, 2, 3, 4]
pre_product[0] = 1 （前面没有元素）
pre_product[1] = pre_product[0] * nums[0] = 1 * 1 = 1
pre_product[2] = pre_product[1] * nums[1] = 1 * 2 = 2
pre_product[3] = pre_product[2] * nums[2] = 2 * 3 = 6
=> pre_product = [1, 1, 2, 6]

第三步：构造后缀乘积数组

for i in range(len(nums) - 2, -1, -1):
    suf_product[i] = suf_product[i + 1] * nums[i + 1]

从后往前遍历，每一步都在后一个后缀的基础上乘上当前的数字。例如：

nums = [1, 2, 3, 4]
suf_product[3] = 1 （后面没有元素）
suf_product[2] = suf_product[3] * nums[3] = 1 * 4 = 4
suf_product[1] = suf_product[2] * nums[2] = 4 * 3 = 12
suf_product[0] = suf_product[1] * nums[1] = 12 * 2 = 24
=> suf_product = [24, 12, 4, 1]

第四步：计算最终答案

for i in range(len(nums)):
    answer[i] = pre_product[i] * suf_product[i]

将前缀和后缀相乘，就得到了除自己外其余数的乘积。

继续上面的例子：

nums = [1, 2, 3, 4]
pre_product = [1, 1, 2, 6]
suf_product = [24, 12, 4, 1]
=> answer[i] = [1*24, 1*12, 2*4, 6*1] = [24, 12, 8, 6]

⏱️ 复杂度分析

• 时间复杂度： O(n)，我们只对数组进行了几次线性遍历。
• 空间复杂度： O(n)，使用了两个辅助数组（前缀和后缀）。通过修改原数组，也可以优化为 O(1)。

代码如下：

class Solution(object):
    def productExceptSelf(self, nums):
        """
        :type nums: List[int]
        :rtype: List[int]
        """
        answer = [1] * len(nums)

        pre_product = [1] * len(nums)
        suf_product = [1] * len(nums)

        # 构造前缀乘积数组
        for i in range(1, len(nums)):
            pre_product[i] = pre_product[i-1] * nums[i - 1]

        # 构造后缀乘积数组
        for i in range(len(nums)-2, -1, -1):
            suf_product[i] = suf_product[i+1] * nums[i + 1]

        for i in range(len(nums)):
            answer[i] = pre_product[i] * suf_product[i]
        
        return answer

执行时间如下：

思路二：
改进一下代码，不再使用两个数组存储前缀乘积和后缀乘积，而是先用answer数组存储前缀乘积，然后用一个变量遍历后缀乘积，并实时地更新answer，这样可以只使用输出数组和一个变量，实现 O(1) 的额外空间复杂度。

优化思路：
既然前缀乘积可以存储在输出数组 answer 中，那么我们可以在第一遍正向遍历中就完成这个任务：

for i in range(1, len(nums)):
    answer[i] = answer[i - 1] * nums[i - 1]

这样，answer[i] 就表示了从 nums[0] 到 nums[i-1] 的乘积，即当前元素左边所有数的乘积。

接下来，在反向遍历时，我们不再使用另一个数组来保存后缀乘积，而是：

• 使用一个变量 current_suf_product 来动态维护当前元素右边的乘积。
• 每次更新完 current_suf_product 后，将其乘到 answer[i] 上。

current_suf_product = 1
for i in range(len(nums)-2, -1, -1):
    current_suf_product *= nums[i + 1]
    answer[i] *= current_suf_product

这一步完成后，answer[i] 就等于 “左边乘积 × 右边乘积”，也就是题目要求的 “除自己外其余元素的乘积”。

代码如下：

class Solution(object):
    def productExceptSelf(self, nums):
        """
        :type nums: List[int]
        :rtype: List[int]
        """
        answer = [1] * len(nums)
        current_suf_product = 1

        # 先将answer构造为前缀乘积数组
        for i in range(1, len(nums)):
            answer[i] = answer[i - 1] * nums[i - 1]

        # 动态更新answer
        for i in range(len(nums)-2, -1, -1):
            current_suf_product *= nums[i + 1]
            answer[i] *= current_suf_product
        
        return answer

执行时间如下，可以看到空间复杂度得到了明显的改善（22.16MB -> 19.88MB）：