扩散模型复习——Diffusion Models Review(Understanding Diffusion Models: A Unified Perspective论文公式推导)

扩散模型复习——Diffusion Models Review(Understanding Diffusion Models: A Unified Perspective论文公式推导)

摘要

本周周报系统性地梳理了扩散模型的理论基础与优化机制，重点围绕《Understanding Diffusion Models: A Unified Perspective》的公式推导展开。内容涵盖生成模型的目标、证据下界（ELBO）的数学推导及其在变分自编码器（VAE）与多层变分自编码器（HVAE/MHVAE）中的应用，深入分析了变分扩散模型（VDM）的优化目标分解为重构项、先验匹配项与去噪匹配项的理论依据。此外，通过加噪过程的闭式解推导与去噪过程的逐步迭代分析，揭示了扩散模型通过神经网络预测原图的核心优化逻辑，为理解其生成机制提供了理论支撑。

Abstract

This review systematically explores the theoretical foundations and optimization mechanisms of diffusion models, focusing on the mathematical derivations in Understanding Diffusion Models: A Unified Perspective. The study covers the objectives of generative models, the derivation of the Evidence Lower Bound (ELBO), and its application in Variational Autoencoders (VAE) and their hierarchical extensions (HVAE/MHVAE). It further dissects the optimization objective of Variational Diffusion Models (VDM) into reconstruction, prior matching, and denoising matching terms. By deriving the closed-form solution of the forward noising process and analyzing the iterative denoising steps, the review highlights the core mechanism of optimizing diffusion models through neural network-based prediction of the original data, offering a unified perspective on their generative principles.

周报内容

1.引言：生成模型的目标

首先是概括性地介绍生成模型的目标以及目前生成模型的类型。

从2个原因充分理解证据下界ELBO（如何推导）：

1. 为什么ELBO的形式如此？
2. 对数似然$logp(x)$中的众多下界中，为什么就选择ELBO作为优化的对象？

2.背景：证据下界, 变分自编码器和多层变分自编码器

这一张主要介绍：

1. VAE为什么叫变分自动编码器 。
2. 深入剖析理解ELBO的2项 。
3. 从高斯分布设定编码器（后验分布） （1）蒙特卡洛 （2）重参数化。

这一张主要介绍:优化目标ELBO的推广

1. 第一个推广模型：HVAE
2. 第二个推广模型：MHVAE

3.变分扩散模型

这一张主要介绍变分扩散模型VDM的表示和优化思路（3个限制条件的深刻理解）

这一张是变分扩散模型VDM的优化目标：ELBO的拆解项含义详解

1. 重构项
2. 先验匹配项
3. 一致项

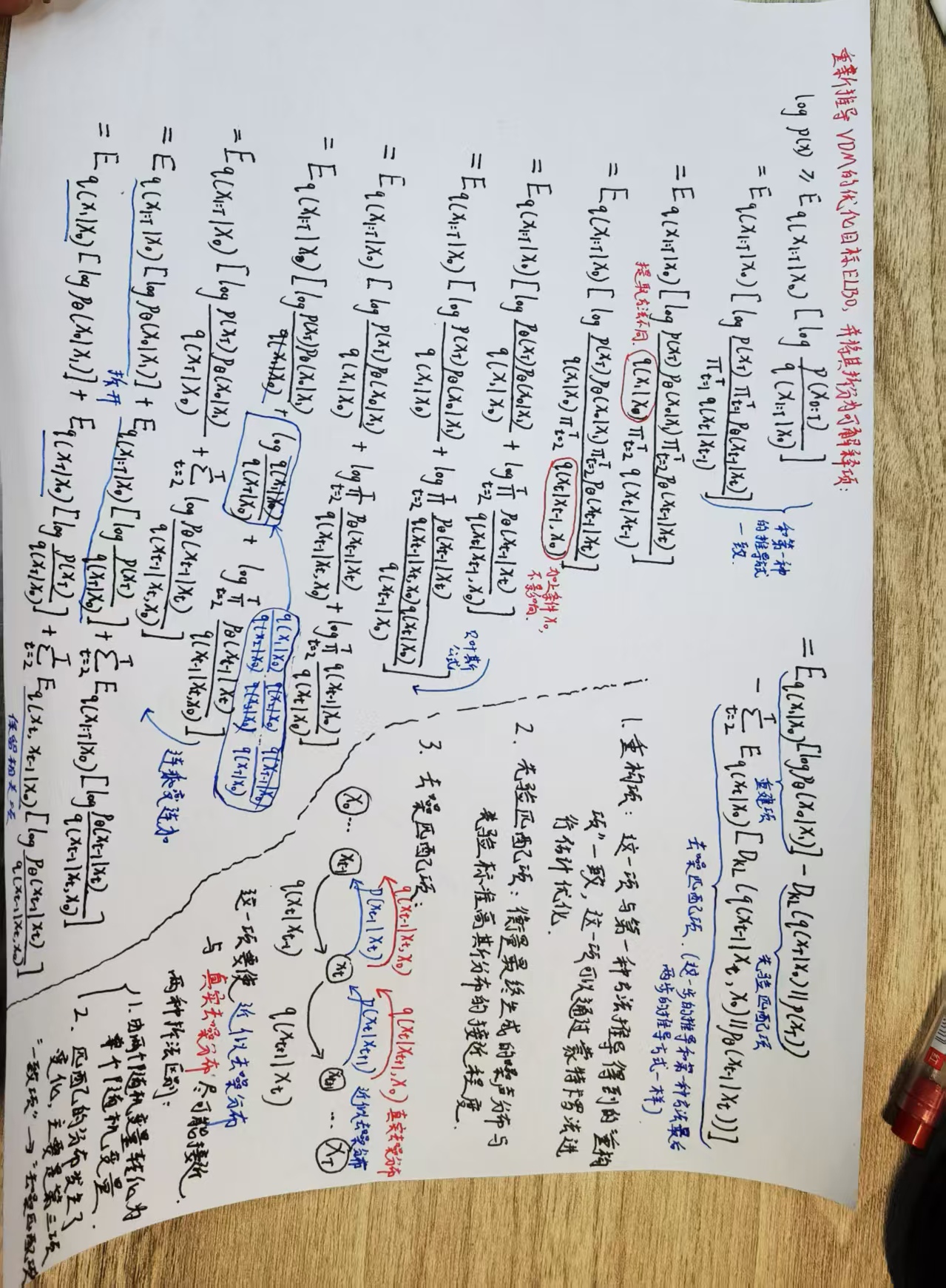
扩散模型的优化核心就是去噪匹配项，这张详细推导了去噪匹配项的由来。

ELBO优化目标的另一种拆解方式：

1. 重构项
2. 先验匹配项
3. 去噪匹配项

这一张介绍加噪过程：为什么只需给定时间步$t$和原图$x_0$就可以直接生成噪图$x_t$？

同时介绍去噪过程：如何由纯噪图逐步去噪变清晰，即从$x_t$到$x_{t-1}$，去推导噪分布表达式。

本周的最后一张，介绍VDM的优化目标转化为利用一个神经网络预测原图$x_0$。

总结

本次周报通过理论推导与公式解析，系统性地总结了扩散模型的核心框架。研究探讨了ELBO在变分推断中的关键作用，揭示了VAE到VDM的扩展逻辑，并深入分析了VDM优化目标中各项的物理意义，尤其是去噪匹配项对模型性能的决定性影响。通过对加噪过程的闭式解与去噪过程的条件分布推导，明确了扩散模型通过逐步噪声预测实现数据生成的内在机制。本次周报主要是复习并深化了对扩散模型理论基础的理解。