用于实时辐射场渲染的3D高斯溅射——3D Gaussian Splatting for Real-Time Radiance Field Rendering

用于实时辐射场渲染的3D高斯溅射——3D Gaussian Splatting for Real-Time Radiance Field Rendering

摘要

本周的工作重点是研究论文《用于实时辐射场渲染的3D高斯溅射》，深入探讨了其提出的3D Gaussian Splatting方法及其在实时渲染中的应用。该方法通过引入3D Gaussian模型和Splatting技术，突破了传统三维场景表示方法的局限性，尤其是在渲染速度和图像质量之间的权衡上表现优异。论文详细介绍了3D Gaussian的数学定义及其在三维几何建模中的优势，并通过光栅化技术将三维场景投影到二维图像，实现了高效的渲染过程。此外，文中提出了交叉优化策略，对高斯模型的各项属性（如三维位置、透明度、协方差矩阵等）进行迭代优化，并结合自适应密度控制策略，有效地解决了重建不足和重建过度的问题。通过基于分块的快速可微光栅化技术，进一步提升了渲染效率，使实时渲染成为可能。实验结果表明，该方法能够在复杂场景中实现高质量的图像渲染，同时显著缩短训练和推理时间，为实时辐射场渲染提供了一种创新性的解决方案。

Abstract

This week focused on the study of the paper “3D Gaussian Splatting for Real-Time Radiance Field Rendering,” which introduces a novel approach to achieve efficient real-time radiance field rendering. This method overcomes the limitations of traditional 3D scene representation techniques, particularly in balancing rendering speed and image quality, by incorporating 3D Gaussian models and splatting techniques. The paper elaborates on the mathematical definition of 3D Gaussian and its advantages in 3D geometry representation, as well as the rasterization process that ensures efficient mapping of 3D scenes to 2D images. Key innovations include an interleaved optimization strategy, which iteratively refines the properties of Gaussian models (e.g., 3D position, opacity, covariance matrix), and an adaptive density control mechanism to address under-reconstruction and over-reconstruction issues. Moreover, the proposed tile-based differentiable rasterization technique significantly accelerates rendering by parallelizing computations and optimizing the rendering pipeline. Experimental results demonstrate the method’s ability to render high-quality images in complex scenes while drastically reducing training and inference time, presenting a groundbreaking solution for real-time radiance field rendering.

1. 预备知识

1.1 三维的几何表示

• 顶点表示(Vertex Representation)：通过最简单和最基础的三维几何表示方法，通过一系列的顶点来定义物体的形状，每个顶点包含了其在三维空间中的坐标信息。通过连接这些顶点，可以形成线、面或体等几何形状。顶点表示适用于表示简单几何形状或离散的点云数据。

• 多边形网格表示(Polygon Mesh Representation)：多边形网格是由连接顶点的边和面组成的结构。它是表示复杂几何形状的一种常见方法。多边形网格通常由三角形或四边形构成，但也可以包含更高阶的多边形。多边形网格可以表示平面几何形状，也可以通过三角剖分等技术表示曲面或复杂形状。

• 参数曲面表示(Parametric Surface Representation)：参数曲面是通过参数化方程来表示的曲面。它使用参数化坐标(通常是二维参数)来描述曲面上的点。参数曲面可以通过数学函数或参数化曲线来生成，例如贝塞尔曲线和贝塞尔曲面。参数曲面表示适用于光滑的曲面和复杂的形状。

• 体素表示(Voxel Representation)：体素是三维空间中的一个像素或体素元素，类似于二维图像中的像素。体素表示将三维空间划分为规则的体素网格，并使用每个体素的属性(如密度、颜色)来表示物体的形状和属性。体素表示适用于体积数据和体绘制应用。NeRF和3D Gaussian splatting主要是使用体素进行三维几何表示。
  

1.2 计算机中的集合表达

目前市面上大部分大型游戏在计算机中都是使用三角网格进行三维显式几何表达，能够借助 GPU 进行快速渲染。但三角网格由于三角形之间或三个顶点之间都是离散的，三角网格的离散性导致其优化存在固有局限性，只能以顶点为单位进行调整，而无法进行更精细的连续优化，从而引发高维度计算难题。

• NeRF ：该系列的方法大多使用光线追踪(ray marching)，速度自然没法和成熟的显式几何+光栅化比。而NeRF在参数优化时一个参数变化对几何的优化可能是一大块也可能是一个小细节。

• 3D Gaussian：使用的椭球形表示可以作为小型可微空间进行优化，不同Gaussian 之间则能够像三角网格一样并行光栅化渲染。可以看成是在可微和离散之间做了一个微妙平衡。

1.3 渲染

图像渲染是将三维场景转换为二维图像的过程。它是计算机图形学领域的一个重要任务，用于生成逼真的图像，以便在计算机屏幕上显示或进行进一步的图像处理。

• 光栅化(Rasterization)：在介绍Splatting之前需要先介绍一下光栅化，光栅化通过找到所有被几何原型所占据的所有像素点然后逐个渲染这些点，得到图像的显示效果。光栅化渲染速度快，用于实时渲染，但渲染效果可能不如体渲染。光栅化的具体过程可以参考：1.（超详细！)计算机图形学 入门篇 3. 光栅化(Rasterization) - 知乎 2. 现代计算机图形学基础二：光栅化（Rasterization） - 知乎

• 体渲染(Volume Rendering)：体渲染把气体等物质抽象成一团飘忽不定的粒子群。光线在穿过这类物体时，其实就是光子在跟粒子发生碰撞的过程。下图是体渲染建模的示意图。光沿直线方向穿过一堆粒子 (粉色部分)，如果能计算出每根光线从最开始发射，到最终打到成像平面上的辐射强度(Nerf中其实可以理解为颜色)，我们就可以渲染出投影图像。而体渲染要做的，就是对这个过程进行建模。为了简化计算，我们就假设光子只跟它附近的粒子发生作用，这个范围就是图中圆柱体大小的区间。体渲染的具体过程可以参考：NeRF入门之体渲染 (Volume Rendering) - 知乎
  

1.4 相机内参和外参

• 相机内参：通常包括焦距$(f_x,f_y)$、主点坐标$(c_x,c_y)$和像素尺寸$(d_w,d_h)$等参数，这些参数描述了相机内部的光学特性，对于理解和控制图像的形成至关重要。
• 相机外参：包括相机的位置和姿态，通常通过相机的内参和一些附加的信息(如相机的镜头畸变系数)来估计。外参的主要作用是将相机坐标系下的点云(即相机捕获的三维空间中的点)转换到世界坐标系下。

在3D Gaussian splatting中，相机的内参和外参被用来将点云投影到图像平面上，这一步叫做splatting。在此过程中，相机的内参帮助我们理解和控制图像的形成，而相机的外参则帮助我们将三维空间中的点映射到图像平面上。这部分的具体过程可以参考：相机内参矩阵、外参矩阵、畸变矩阵-CSDN博客

1.5 3D Gaussian

3D Gaussian的公式为：

$$N_{{\mu }_x,{\sigma }_x,{\mu }_y,{\sigma }_y,{\mu }_z,{\sigma }_z}\left(x,y,z\right)=\frac{1}{(\sqrt{2\pi }{)}^3{\sigma }_x{\sigma }_y{\sigma }_z}\exp \left(-\frac{{\left(x-{\mu }_x\right)}^2}{2{{\sigma }_x}^2}-\frac{{\left(y-{\mu }_y\right)}^2}{2{{\sigma }_y}^2}-\frac{\left(z-{\mu }_z\right)}{2{{\sigma }_z}^2}\right)$$

但这其实是分量$x$，$y$，$z$互相独立的特例，此时的模型坐标系和世界坐标系平行。不过这种特例可以帮助理解3D Gaussian：试想一个实心椭球，将它沿某一条轴切开后会得到一个椭圆，这个椭圆其实是无限大的，每一层的密度都不相同，这个切面就是二维高斯分布的等线图：

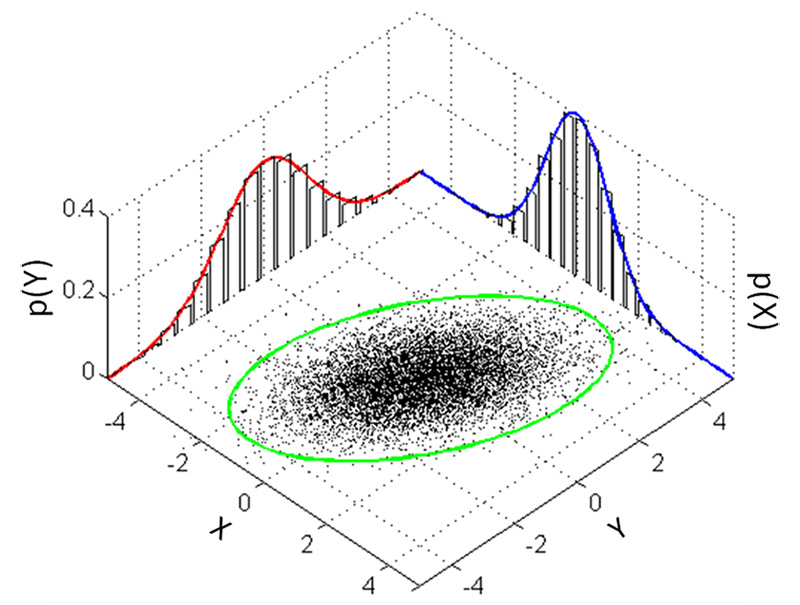
3D Gaussian 也叫三维高斯分布或三维正态分布，是统计学中一种特殊的多维正态分布，通常用来建模具有连续性随机性的现象，如图像处理、统计建模、机器学习等领域。3D Gaussian 能够涵盖空间中任意形状的椭球，包括平移、旋转。3D Gaussian 在三维空间中定义了一个概率分布，标准模型数学表示如下：$$G_s\left(x\right)=\frac{1}{(\sqrt{2\pi }{)}^3\det (\Sigma )}exp\left(-\frac{1}{2}{\left(x-\mu \right)}^T{\Sigma }^{-1}(x-\mu )\right)$$

其中$x=[a,b,c{]}^T$是三维坐标向量；$\mu$是椭球的中心，控制椭球的位置平移；$\Sigma =\left[\begin{array}{ccc}{\sigma }_a^2& \mathrm{Cov}(a,b)& \mathrm{Cov}(a,c)\\ \mathrm{Cov}(b,a)& {\sigma }_b^2& \mathrm{Cov}(b,c)\\ \mathrm{Cov}(c,a)& \mathrm{Cov}(c,b)& {\sigma }_c^2\end{array}\right]$是协方差矩阵，控制椭球在三维方向的伸缩和旋转。

论文中的 3D Gaussian 表示去掉了指数部分前面的尺度系数(因为系数不影响椭球的几何形状) 和均值 (因为每个点云有自己的位置$p$ )，方便旋转放缩。于是 3D Gaussian 表示如下：

$$G(x)=exp\left(-\frac{1}{2}{x}^T{\Sigma }^{-1}x\right)$$

因此只要确定了$\Sigma$就可以确定一个椭球的形状。但需要注意的是，三维高斯分布的协方差矩阵$\Sigma$必须是半正定的才有数学意义。论文中使用的是各向异性$\Sigma$，即在不同方向上具有不同方差值。各向异性协方差更有利于优化，因为它能够适应不同方向的变化，具有更精确的建模、更好的参数优化和更紧凑的表示。

1.6 Splatting

Splatting 是一种用于光栅化 3D 对象（如前文讨论的椭球）的技术。这些 3D 对象被映射到投影平面后得到的 2D 图形称为 splat，类似于一个点、圆、矩形或其他形状，就像雪球打在墙上留下的印记，能量从中心向外扩散并减弱。这个过程可以在 GPU 上并行处理，因为每个 Splat 之间是独立的。

Splatting 可以将三维空间中的点投影到二维图像平面上，这些投影的数据点以某种方式在图像上产生视觉效果，从而呈现在最终的渲染图像中。Splatting 通常并不是由传统的图形硬件管线自动执行，而是需要相对复杂的GPU编程，通常由图形开发者在需要时自行实现。

2. 基本思想

• 传统的三维场景表示方法需要使用网格或点云进行三维重建，近几年出现的 NeRF 可以直接进行场景的视图合成。

• 但 NeRF 想要生成高质量的视图需要花大量的时间进行训练和渲染，因此在实际应用中需要对质量和速度进行权衡。并且目前还没有方法能够达到实时显示的效果。

• 文章提出了一种新方法—— 3D Gaussian Splatting，同时保证了图像的质量和渲染的速度：3D Gaussian 模型能够表示先进的视觉质量和高效的训练速度，Splatting 技术能够确保高分辨率的实时渲染。

整个模型的输入是 SfM 点云表示的一组静态场景的照片和相应机位，使用点云初始化一组 3D Gaussian 模型。 3D Gaussians 能够合理紧凑地表示三维场景，颜色由球谐系数 SH 表示。 通过交叉优化 3D Gaussian 模型参数和自适应控制得到场景表示。本文方法高效的关键在于 3D Gaussian 的光栅化，通过各向异性的 Splatting 和 $\alpha$-blending 技术，能够快速合成渲染图像。

2.1 3D Gaussian Splatting

引入 3D Gaussian 来表示场景，将其初始化为摄像机标定产生的 SfM 稀疏 点云。这样既能保持辐射场的理想特性以便优化，又能避免在空白空间中进行不必要的计算。

3D Gaussian 的 光栅化 (rasterization) 过程如下：先使用 Splatting 技术将 3D Gaussian 投影到 2D 图像，然后使用标准的 $\alpha$-blending 技术快速合成渲染图像。这意味着 3D Gaussian 的三维场景表示可以转换为二维图像，以供渲染和可视化。

$\alpha$-blending: 一种用于合成两幅或多幅图像以获得混合效果的图像处理技术。在$\alpha$-blending 中，每幅图像都被赋予一个权重参数$\alpha \left(0\le \alpha \le 1\right)$，表示每幅图像在最终合成中的贡献程度，0 表示完全使用第一幅图像，1 表示完全使用第二幅图像，而在 0 到 1 之间的中间值则表示混合两幅图像。

$\alpha$-blending 可以用于各种图像处理任务，包括图像叠加、过渡效果、颜色校正等，以实现图像的合成与编辑。一个典型应用就是创建图像淡入淡出效果，其中一个图像逐渐淡出，同时另一个图像逐渐淡入，通过调整$\alpha$参数的值来实现平滑过渡。$\alpha$-blending 也可以用于将两个图像合成成一个，以产生具有新特性的图像，如合成景深效果、融合不同光照条件下的图像等。

2.2 交叉优化

交叉优化 (interleaved optimization) 3D Gaussian 的属性和 Gaussians 的自适应 密度控制 (density control)，尤其是优化 各向异性协方差 (anisotropic covariance)，以实现场景的精确表示。

可以优化的 3D Gaussian 点云属性包括：三维位置$p$、透明度$\alpha$ (其实就是$\alpha$-blending 中的权重参数)、各向异性协方差$\Sigma$、球谐系数 SH (spherical harmonic coefficients) 等。

球谐函数(Spherical Harmonics): 用于描述在球面上的角度相关函数的一组正交函数。球谐函数由两个角度参数(极角$\theta$和方位角$\varphi$)和两个整数参数(轨道量子数$l$和磁量子数$m$)定义，通常表示为$Y_{lm}\left(\theta ,\varphi \right)$。球谐函数在球坐标系中是正交的，这意味着在给定的球面上，它们的内积为零。这种正交性质使得球谐函数在处理球对称问题时非常有用。更多解释见：球谐函数介绍 (Spherical Harmonics)、球面高斯介绍 (Spherical Gaussian) 。

球谐系数 (Spherical Harmonics Coefficients): 一组基于球谐函数的系数，用于展开和描述球对称的函数或信号。球谐系数$a_{lm}$描述了一个给定函数在球谐函数基础上的分解，其表达式如下：

$$f(\theta ,\varphi )=\sum _{l=0}^{\infty }\sum _{m=-l}^l{a}_{lm}{Y}_{lm}\left(\theta ,\varphi \right)$$

这个公式表示，任意球对称的函数$f(\theta ,\varphi )$可以通过球谐函数的组合进行表示。对于给定的三维高斯分布，可以通过与球谐函数的积分来计算具球谐系数：

$$a_{lm}=\iiint Y_{lm}\left(\theta ,\varphi \right)\cdot f\left(\theta ,\varphi ,r\right)r^2\sin \theta drd\theta d\varphi$$

其中，$Y_{lm}\left(\theta ,\varphi \right)$是球谐函数，$f(\theta ,\varphi ,r)$是高斯分布的三维表示，$r$是径向距离，$\theta$是极角，$\varphi$是方位角。

2.3 快速可微光栅化

使用 GPU 进行快速、可微的渲染，支持各向异性 Splatting 和快速反向传播。因此能够加速训练和实时渲染。

3. 3D Gaussian Splatting

鉴于 3D Gaussian 可微、便于投影到二维、显示地支持快速渲染等优点，用其作为场景表示。使用一个三维的满协方差矩阵初始化 3D Gaussian：

$$G(x)=exp\left(-\frac{1}{2}{x}^T{\Sigma }^{-1}x\right)$$

光栅化时需要将三维场景变换到二维空间，作者希望 3D Gaussian 在变换中保持分布 (不然光栅完和高斯没关系的话一直以来的努力都白费了)，这难免需要更多限制。View 变换$W$ 主要是旋转和平移，都是仿射 (affine)的，不会有问题；但 Project 变换不是仿射的，因此文中使用 Project 变换的仿射近似雅可比矩阵$J$替代 Project 变换。于是得到摄像机坐标下的协方差矩阵${\Sigma }^{\prime }:$

$${\Sigma }^{\prime }=JW\Sigma W^T{J}^T$$

但$\Sigma$不能直接优化，因为$\Sigma$必须是 半正定 (semi-definite) 的 3D Gaussian 才有意义。于是文中将$\Sigma$表示为球变换到椭球的过程：将球按轴向先放缩$S$再旋转$R$ (注意顺序，是先放缩再旋转，椭球的对称轴一直是模型空间的 xyz 轴，互相垂直)。因此$\Sigma$初始化如下：

$$\Sigma =RS{S}^T{R}^T$$

于是在训练过程中使用梯度下降对参数$\Sigma$进行优化时需要继续将梯度传递到$S$和$R$进行优化。

如前文所述，各向异性协方差更适合优化：能够优化 3D Gaussian 以适应场景中不同形状的几何形状，从而产生一个紧凑的表示。如下图所示，将 3D Gaussian 渲染的图像缩小 60% 后细节仍然清晰可见，说明其对复杂细节较强的拟合能力：

4. 交叉优化

本文的核心是对 3D Gaussian 的优化，优化的目的是创建一组密集的 3D Gaussian 以精确地表示场景。优化的参数包括：三维位置$p$、透明度$\alpha$、各向异性协方差$\Sigma$和球谐系数 SH (spherical harmonic coefficients)。这些参数的优化和自适应控制高斯模型交替进行 (也可以理解为在参数优化的过程中周期性地进行致密化)。

4.1 参数优化

由于 3D 投影到 2D 的模糊性，渲染图像中的几何体可能会被放错位置。因此，优化过程中需要能够创建几何体，并且在错误位置处销毁或移动几何体。

参数优化使用 SGD 连续迭代完成，每一轮迭代时都会渲染图像并将其与真实的训练视图做比较。$\alpha$ 使用 Sigmoid 激活函数来限制$(0,1)$的范围；$\Sigma$使用指数激活函数激活；$p$使用指数衰减调度技术(exponential decay scheduling technique) 进行优化。模型的损失函数是 $L_1$ 与 D-SSIM 项的组合：

$$\mathcal{L}=(1-\lambda ){\mathcal{L}}_1+\lambda {\mathcal{L}}_{\mathrm{D}-\mathrm{SSIM}}$$

SSIM (Structural Similarity Index)：结构相似性指标，一种用于衡量两幅图像之间结构相似性的指标。它不仅考虑了两幅图像的亮度和对比度差异，还考虑了它们的结构信息。SSIM 指标取值范围通常在 $[-1,1]$ 之间，越接近 1 表示两幅图像越相似，越接近 -1 表示两幅图像越不相似。计算 SSIM 时，先将图像分成许多小块，然后对每个块应用一个一维的高斯窗口（这个窗口的目的是加权不同位置的像素，使得中心像素附近的像素对 SSIM 的贡献更大）再对每个块计算亮度、对比度和结构相似性，最后将所有块的亮度、对比度和结构相似性的平均值组合起来，得到整体的 SSIM 值。

D-SSIM (Dissimilarity Structural Similarity Index)：结构相异性指标，用于衡量两幅图像之间结构差异性。
$$D-SSIM=\frac{1-SSIM}{2}$$

4.2 自适应控制

在 3D Gaussian Splatting 中，场景表示是通过多个高斯模型叠加而成的。在早期迭代次数较少时，会出现重建不足 (under-reconstruction) 的问题，即高斯模型没有完全覆盖小规模的几何体，此时需要复制高斯模型进行覆盖；在后期迭代次数较多时，会出现重建过度 (over-reconstruction) 的问题，即高斯模型超出小规模几何体的范围，此时需要将该高斯模型一分为二。这就是自适应控制 Gaussians：

从初始化 Gaussians 为稀疏的 SfM 点云开始，通过自适应地控制高斯模型的数量和它们在单位体积上的密度，逐渐从稀疏的高斯模型集合过渡到更密集且能够更好地表示场景的集合。该过程主要关注under-reconstruction 和 over-reconstruction 的区域，即具有较大的视图空间位置梯度的区域。直观理解来看，是因为这些区域尚未完全重建好，因此优化算法试图移动高斯函数以进行修正。under-reconstruction 和 over-reconstruction 的区别是 over-reconstruction 区域的Gaussian 方差大，因为数据的变化幅度较大。对于视图空间的位置梯度大于阈值${\tau }_{\mathrm{pos}}$的区域，需要对该高斯模型进行致密化(densify)操作：

• under-reconstruction 区域：高斯模型没有完全覆盖小规模的几何体，此时需要复制高斯模型并将其沿位置梯度方向移动，以覆盖几何体。
• over-reconstruction 区域：高斯模型超出小规模几何体的范围，此时需要将该拆分高斯模型并覆盖几何体。

然而，这种体积表示法在优化过程中可能会因为相机附近的漂浮物而陷入困境，从而导致高斯密度不合理的增加。一个有效的调节方法是每 3000 次迭代就将$\alpha$值设为接近零，然后再根据上述优化过程逐渐提高$\alpha$值。此外，每100次迭代就剔除透明的高斯分布 (即$\alpha$小于阈值${ϵ}_{\alpha }$ )以限制高斯模型的总数量。

5. 快速可微光栅化

直接 Splatting 显然没法实现高帧率的渲染效果，下面介绍文中是如何进行光栅化的。Gaussians 快速可微光栅化是为了快速实现整体渲染和排序，从而实现近似$\alpha$-blending 并且不再限制能够接收梯度的 splats 的数量。为了达到目的，对 Gaussian splats 进行分块 (tile) 处理，将该光栅化过程命名为基于分块的光栅化(tile-based rasterization)。

1. 首先将 2D 屏幕分割成$16\times 16$个 tile，然后为每个 tile 筛选 视锥体 (view frustum) 内的 3D Gaussian：

   • 每个视锥体内只保留置信度大于 99% 的高斯模型；
   • 设置一个保护带 (guard band) 剔除位于极端位置的高斯模型，如均值接近近平面或在视锥体之外；

   剔除视锥体以外的高斯模型可以节省大量的计算资源，提高渲染速度。

2. 根据每个 Gaussian 重叠的 tile 数量来实例化，为其分配 key 值（key 值结合了该 Gaussian 所在 tile 的 ID 和对应视域的深度）；

3. 使用 GPU Radix sort 根据 key 值对 Gaussians 进行排序（其实就是按高斯模型到图像平面的深度值）；

   传统光栅化渲染管线只能逐像素进行，将三角网格分解为像素，并经过颜色插值、深度测试等一系列的像素处理步骤，最终将渲染结果呈现在屏幕上。

4. 将排好序的 Gaussians 从近到远向对应 tille 上做 Splatting。然后在每个 tile 上对高斯模型留下的splat 做堆叠 (类似$\alpha$-blending,累积$\alpha$和$\mathbf{c}$),直到所有像素的不透明度都饱和($\alpha =1)$ 。该过程可以表示为：

   $$\mathbf{C}=\sum _{i\in \mathcal{N}}{\mathbf{c}}_i{\alpha }_i\prod _{j=1}^{i-1}\left(1-{\alpha }_j\right)$$

   为每个 tile 都单独开了一个线程块，因此每个 tile 上的光栅化过程可以并行执行。图像中某一个像素不透明度达到饱和后，线程块就停止对该像素的处理。

5. 优化参数时，按每个 tile 堆叠的 splat 对应的 Gaussians 的顺序反向传播；

本节就是 3D Gaussian Splatting 的渲染过程。在合成新视图时，只需要指定一个视角，就可以使用视锥体筛选 3D Gaussian 点云，然后光栅化得到 2D 图像。

总结

本次周报学习了一种基于3D高斯模型的创新性实时辐射场渲染方法，充分利用了3D Gaussian在场景表示中的灵活性和紧凑性，结合Splatting技术，实现了高效的光栅化渲染。通过数学形式化和实验验证，作者证明了3D Gaussian可以以较低的计算成本保留场景的几何和辐射细节。在渲染过程中，光栅化技术将三维场景投影到二维图像，配合快速的$\alpha$-blending算法实现了高分辨率的实时渲染。同时，交叉优化策略对高斯模型的三维位置、透明度、协方差矩阵和球谐系数进行了全面优化，并采用自适应密度控制解决了高斯模型在场景表示中的稀疏性和冗余问题。基于分块的快速可微光栅化进一步加速了渲染过程，通过剔除视锥体外的高斯分布和GPU并行计算，确保了实时性能。实验结果表明，该方法能够在多种复杂场景下生成清晰且真实感强的图像，并且渲染速度大幅提升，为实时渲染和视图合成任务提供了一个高效且通用的解决方案。这项研究不仅在理论上证明了3D Gaussian Splatting的可行性，还为实际应用提供了切实可行的技术框架，具有重要的研究价值和应用潜力。

参考

论文原文：3D Gaussian Splatting for Real-Time Radiance Field Rendering
3D Gaussian Splatting：用于实时的辐射场渲染

3d Gaussian splatting笔记