欧拉 函数

一、欧拉函数引入

什么是互质
如果两个正整数，除了1以外，没有其他公因子，我们就称这两个数是互质关系（coprime）。比如，15和32没有公因子，所以它们是互质关系。这说明，不是质数也可以构成互质关系。

什么是欧拉函数
任意给定正整数n，请问在小于等于n的正整数之中，有多少个与n构成互质关系。

计算这个值的方法叫做欧拉函数，用φ(n)表示。
例如，在1到8之中，与8形成互质关系的是1、3、5、7，所以 φ(n) = 4。

二、欧拉函数的定义

定义： 欧拉函数φ(n)是一个定义在正整数集上得函数，φ(n)的值等于序列0，1，2，…，n-1中与n互素的数的个数。

注：φ(1)=1（和1互质的数(小于等于1)就是1本身）。

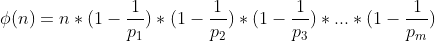
三、欧拉函数一些公式，性质

1. p为质数,n为大于0自然数
   φ( p)=p-1

2. 欧拉函数是积性函数,但不是完全积性函数。
   若m,n互质
   if(m%p==0) φ(p*m) = φ(m)p
   else φ(pm) = φ( p)*φ(m)

   if(m&1) φ(2*m) = φ(m)
   else if(m>2) φ(m)为偶数
   φ(pm)=φ(pm)-φ(pm-1)

3. 当且只当n可以分解成两个互质的整数之积，n = p1 × p2，则φ(n) = φ(p1p2) = φ(p1)φ(p2)

特别的，对于两个素数p,q， φ(pq)=(p-1)(q-1)。(RSA算法应用）

4. 若n是质数p的k次幂，φ(n)=pk-pk-1=(p-1)pk-1，因为除了p的倍数外，其他数都跟n互质。

   φ(n)=pk-pk-1=(p-1)pk-1

5.求和

四、三种求解方法

gcd求解

int get_phi(int n){
	int res=1;
	for(int i=2;i<n;i++)
		if(__gcd(i,n)==1)
			res++;
}

O(sqrt(n))求解

int phi(int n) {
	int res=n;
	for(int i=2; i*i<=n; i++) {
		if(n%i==0) {
			res=res*(i-1)/i;
			while(n%i==0)
				n/=i;
		}
	}
	if(n>1)
		res=res*(n-1)/n;
	return res;
}

O(n)求解

void get_phi(int n){
	phi[1]=1;
	for(int i=2;i<=n;i++){
		if(!vis[i]){
			prime[cnt++]=i;
			phi[i]=i-1;//φ( p)=p-1
		}
		for(int j=0;j<cnt&&prime[j]*i<=n;j++){
			vis[prime[j]*i]=1;
			if(i%prime[j]==0){//性质if(m%p==0) φ(p*m) = φ(m)*p   else φ(p*m) = φ(p)*φ(m)
				phi[prime[j]*i]=phi[i]*prime[j];
				break;
			}
			//phi[prime[j]*i]=phi[i]*phi[prime[j]];
			phi[prime[j]*i]=phi[i]*(prime[j]-1);//phi[j]=j-1
		}
	}
}




void get_phi(int n){
	phi[1]=1;
	for(int i=2;i<=n;i++){
		if(!vis[i]){
			prime[++cnt]=i;
			phi[i]=i-1;//φ( p)=p-1
		}
		for(int j=1;j<=cnt&&prime[j]*i<=n;j++){
			vis[prime[j]*i]=1;
			if(i%prime[j]==0){//性质if(m%p==0) φ(p*m) = φ(m)*p   else φ(p*m) = φ(p)*φ(m)
				phi[prime[j]*i]=phi[i]*prime[j];
				break;
			}
			//phi[prime[j]*i]=phi[i]*phi[prime[j]];
			phi[prime[j]*i]=phi[i]*(prime[j]-1);//phi[j]=j-1
		}
	}
}

欧拉函数最全总结

欧拉函数，欧拉定理，欧拉降幂

五、 题目

一、月月给华华出题

牛客：月月给华华出题

题目描述
因为月月是个信息学高手，所以她也给华华出了一题，让他求：
∑Ni=1igcd(i,N)∑i=1Nigcd(i,N)
但是因为这个式子实在太简单了，所以月月希望华华对N=1,2,…,n各回答一次。华华一脸懵逼，所以还是决定把这个问题丢给你。

输入描述:
一个正整数n。
输出描述:
输出n行，第i行表示N=i时的答案。

题解1

题解2

Code:

const int maxn = 1e6+7;

ll phi[maxn];
bool vis[maxn];
ll prime[maxn];
ll cnt;
ll ans[maxn];

void get_phi(int n){
	phi[1]=1;
	for(int i=2;i<=n;i++){
		if(!vis[i]){
			prime[++cnt]=i;
			phi[i]=i-1;
		}
		for(int j=1;j<=cnt&&prime[j]*i<=n;j++){//若j=0;j<cnt显示浮点数错误（出现除数为0的情况）
			vis[prime[j]*i]=1;
			if(i%prime[j]==0){
				phi[prime[j]*i]=phi[i]*prime[j];
				break;
			}
			//phi[prime[j]*i]=phi[i]*phi[prime[j]];
			phi[prime[j]*i]=phi[i]*(prime[j]-1);
		}
	}
}
int main() {
	
	ll n;
	cin>>n;
	get_phi(n);
	for(int i=1;i<=n;i++){
		for(int j=i;j<=n;j+=i){
			ans[j]+=phi[i]*i/2;
		}
	}
	for(int i=1;i<=n;i++){
		cout<<ans[i]+1<<endl;
	}
	return 0;
}

二、Poj2407（套用模板，简单题）

Poj2407

简单题，直接套用模板即可

int main() {
	ll n;
	ll res=n;
	while(cin>>n&&n) {
		res=n;
		for(int i=2; i*i<=n; i++) {
			if(n%i==0) {
				res=res*(i-1)/i;
				while(n%i==0)
					n/=i;
			}
		}
		if(n>1)
			res=res*(n-1)/n;
		cout<<res<<endl;
	}
	return 0;
}

三、Poj2478（模板求和问题）

Poj2478

模板求和问题

复杂度 O(nlogn)

类似筛法求素数

const int maxn = 1e6+7;
ll euler[maxn];
ll ans[maxn];
void eulerr(){
	euler[1]=1;
	for(int i=2;i<maxn;i++)
		euler[i]=i;
	for(int i=2;i<maxn;i++){
		if(euler[i]==i){
			for(int j=i;j<maxn;j+=i){
				euler[j]=euler[j]*(i-1)/i;
			}
		}
	}
} 

int main(){
	eulerr();
	ans[1]=0;
	for(int i=2;i<maxn;i++){
		ans[i]=ans[i-1]+euler[i];
	}
	int n;
	while(cin>>n&&n){
		cout<<ans[n]<<endl;
	}
	return 0;
}
*/ 

四、Poj1248（扩展：原根）

Poj1248

这个题目实质就是问m有多少个原根

原根 百度解释

简单来说，当模m有原根时，原根的个数是φ(φ(m))
依据欧拉函数性质，φ(m) = phi[m] = m-1；
所以，答案为 phi[m-1]

Code

int get_phi(int n){
	int res=n;
	for(int i=2;i*i<=n;i++){
		if(n%i==0){
			res=res*(i-1)/i;
			while(n%i==0){
				n/=i;
			}
		}
	}
	if(n>1){
		res=res*(n-1)/n;
	}
	return res;
}

int main(){
	int n;
	while(cin>>n){
		cout<<get_phi(n-1)<<endl;
	}
	return 0;
}

五、hdu 1787 （模板题 （求不互质））

hdu1787

求1~(n-1)与n不互质的数

Code

int get_phi(int n){
	int res=n;
	for(int i=2;i*i<=n;i++){
		if(n%i==0){
			res=res*(i-1)/i;
			while(n%i==0){
				n/=i;
			}
		}
	}
	if(n>1){
		res=res*(n-1)/n;
	}
	return res;
}

int main(){
	int n;
	while(cin>>n&&n){
		cout<<n-1-get_phi(n)<<endl;//减去1和互质的个数 
	}
	return 0;
}

六、Poj 3090

Poj3090

题解

首先，题目主要是求从0,0能看到的点的个数。

先考虑只有1×1的时候，三个点，根据图明显看出，只需要计算下三角，结果=下三角的个数×2再加1（斜率为1的点）。

那么我们只需要计算斜率从0到1之间的个数就行了，不包括1，包括0.结果设为sum，那么最终就是2*sum+1.

1×1只有一个斜率为0的

2×2斜率有0,1/2（0已经算过了，以后不再算了），其实就多了一个斜率为1/2的。

3×3的时候，有1/3,2/3两个，比以前多了2个

4×4的时候，有1/4,2/4（1/2已经有过了）,3/4，所以也是2个

5×5的时候，有1/5,2/5,3/5,4/5，之前都没有，所以多了4个

6×6得到时候，有1/6,2/6（1/3已经有了）,3/6(1/2已经有了),4/6(2/3已经有了),5/6，所以只剩2个。
。

。

。

从上面可以发现一个规律，对于n×n，可以从0,0连接到（n,0）到(n,n)上，斜率将会是1/n,2/n…(n-1)/n;

凡是分子和分母能够约分的，也就是有公约数，前面都已经有过了。所以每次添加的个数就是分子和分母互质的个数。

Code

const int maxn = 1e6+7;

int phi[maxn];
void eulerr() {//套用模板
	phi[1]=1;
	for(int i=2; i<maxn; i++)
		phi[i]=i;
	for(int i=2; i<maxn; i++) {
		if(phi[i]==i) {
			for(int j=i; j<maxn; j+=i) {
				phi[j]=phi[j]*(i-1)/i;
			}
		}
	}
}

int main() {
	eulerr();
	int t;
	int n;
	cin>>t;
	for(int i=1; i<=t; i++) {
		cin>>n;
		int res=0;
		for(int j=1; j<=n; j++) {
			res+=phi[j];
		}
		res=res*2+1;
		cout<<i<<" "<<n<<" "<<res<<endl;
	}
	return 0;
}