【算法设计与分析】6 最大流应用问题

大期末的手头还2个老师让自学的不知道从哪里爬起的嵌入式项目，我居然还有心思考虑自己的职业生涯来写博客，略感讽刺哈哈哈哈

目录

概览

最大流问题

割

最大流最小割

最大流算法：Ford-Fulkerson算法

残存网络——残存容量 ​编辑【点u到点v】

Ford-Fulkerson算法：

值班问题 

实例化参数，生成数据。

求解

设计流网络

流网络最大流——值班问题

基于生成的数据，计算出排班的方案。

算法优化：DINIC算法（BFS分层dfs）

数据处理

结论：

---

概览

1. 最大流算法思想。
2. 最大流算法求解应用问题。

最大流问题

图G（V,E）【V为顶点集合，E为边集合】的各边（u-v）的权重（运载能力c(u,v)）都是非负数，则称为流网络，它具备源节点s和汇聚点t。我们希望获得基于各点运载能力限制情况下，从s到t能运输的最大流量|f|max（最大流）。

除了s和t，其他结点的流进量等于流出量。同时，f(u,v) <= c(u,v)。

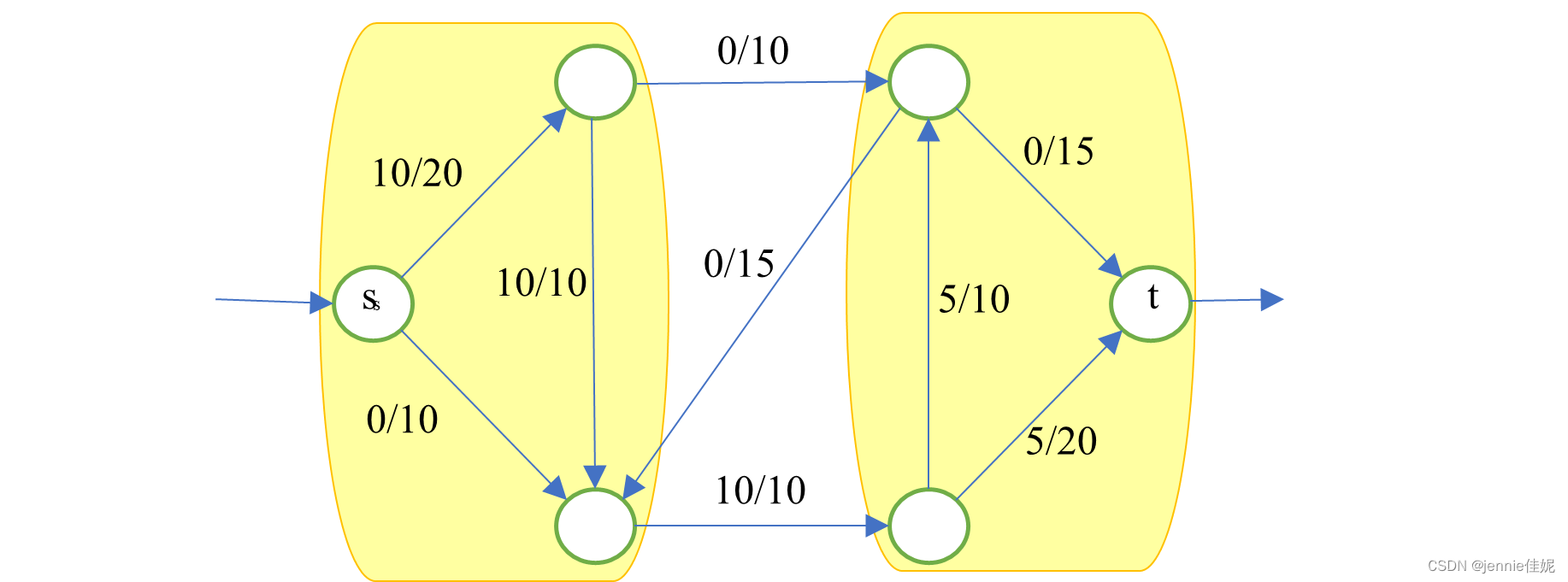
 图表 1 流网络

割

将点分为2个集合(S，S’)，且s和t分别位于不同集合。

从S到S’的最大容量为割的容量cap(S,S’)，注意有方向性。如图中黄色表示，cap(S,S’)=5+10=15，cap(S’,S)=15。我们需要找到最小割，它可以帮助我们求解最大流问题。

最大流最小割

最小割>=最大流，因为流必须从最小割一个集合流向另一个集合，那么必定受最小割容量限制。

最大流算法：Ford-Fulkerson算法

求最大流即找到一种符合个点流量限制的、多条不交叉的从s到t的路径，使最终获得的流量最大。

我们可以通过dfs深度优先搜索获得从s到t的路径，但如果要获得符合条件的最优路径组合，需要有一种纠错机制来判断每次获得路径是否是组合里的。

Ford-Fulkerson算法即提供这样一种纠正方法。对于每次获得的路径（增广路径），我们可以将该路径反向（由原流网络变为残留网络），看是否能于剩余量形成连通路径（根据当前获得的残留容量）。如果有需要减去改变，重复操作，模拟纠错过程。最后完全没有连通路径时即计算完毕。

该过程可抽象为公式如下：

• 残存网络——残存容量 【点u到点v】

如果原图有边 【边上容量限制为c(u，v)】，那么流量需要反向，即u->v边上流量【原f(u，v)】变为v->u边上的流量限制，即c(v，u)= f(u，v)；而此时c(u,v)也少了原f(u，v)这部分流量，于是c(u，v)-=f(u，v)。

基于上面的公式及解释，我们是可以将流网络转换为对应残留网络：

 图表 2 残留网络

• Ford-Fulkerson算法：

从0流量出发，找到增广路径，流更新获得新的残留网络；如果新的残留网络仍然存在增广路径，那么继续重复直到找不到。最后可获得最大流。

• 如下图所示模拟了该过程，第1次选定增广路径为s->a->c->d->t，f=10。
• 接着得到其残留网络（图2，），接着第2次选定增广路径为s->a->b->t，f=10。
• 此时残留网络无增广路径，由于反向，所以流向s的最大流20为最终结果。

 图表 3 Ford-Fulkerson算法

值班问题 

一个医院有n名医生，现有 k 个公共假期需要安排医生值班。每一个公共假期由若干天（假日）组成，第 j 个假期包含的假日用 Dj  表示，那么需要排班的总假日集合为 D=∪j=1kDj 。例如，“五一”假期由5月1日至5月7日一共7个假日组成。“元旦”假期由1月1日至1月3日一共3个假日组成。

每名医生 i  可以值班的假日集合是 Si ，Si⊆D 。例如，李医生可以值班的假日集合包括“五一”假期中的5月3日、5月4日和“元旦”假期中的1月2日。

设计一个排班的方案使得每个假日都有一个医生值班并且满足下面两个条件：

1. 每个医生最多只能值班c 个假日；
2. 每个医生在一个假期中只能值班1个假日。例如，安排李医生在“五一”假期中的5月4日值班。

根据上述场景完成下面任务：

• 实例化参数，生成数据。

答：为了方便后面算法效率的统计，我们假定每个假期有5天，每个医生从中选取3天作为可值班。因此可得到n*c>=k*5，则c>=k*5/n。为此我们同一假定c=10*k/n。

• 求解

设计流网络

答：根据问题给出的信息，不难推测出每个医生和每个具体节假日会是节点。

流网络的定义原理处有提及，这里不再赘述。那么根据定义我们需要设定源点s和汇聚点t。那么我们可以设定源点s指向所有医生节点，而所有节假日最后指向汇聚到t。各个医生与可值班的假日存在有向边。

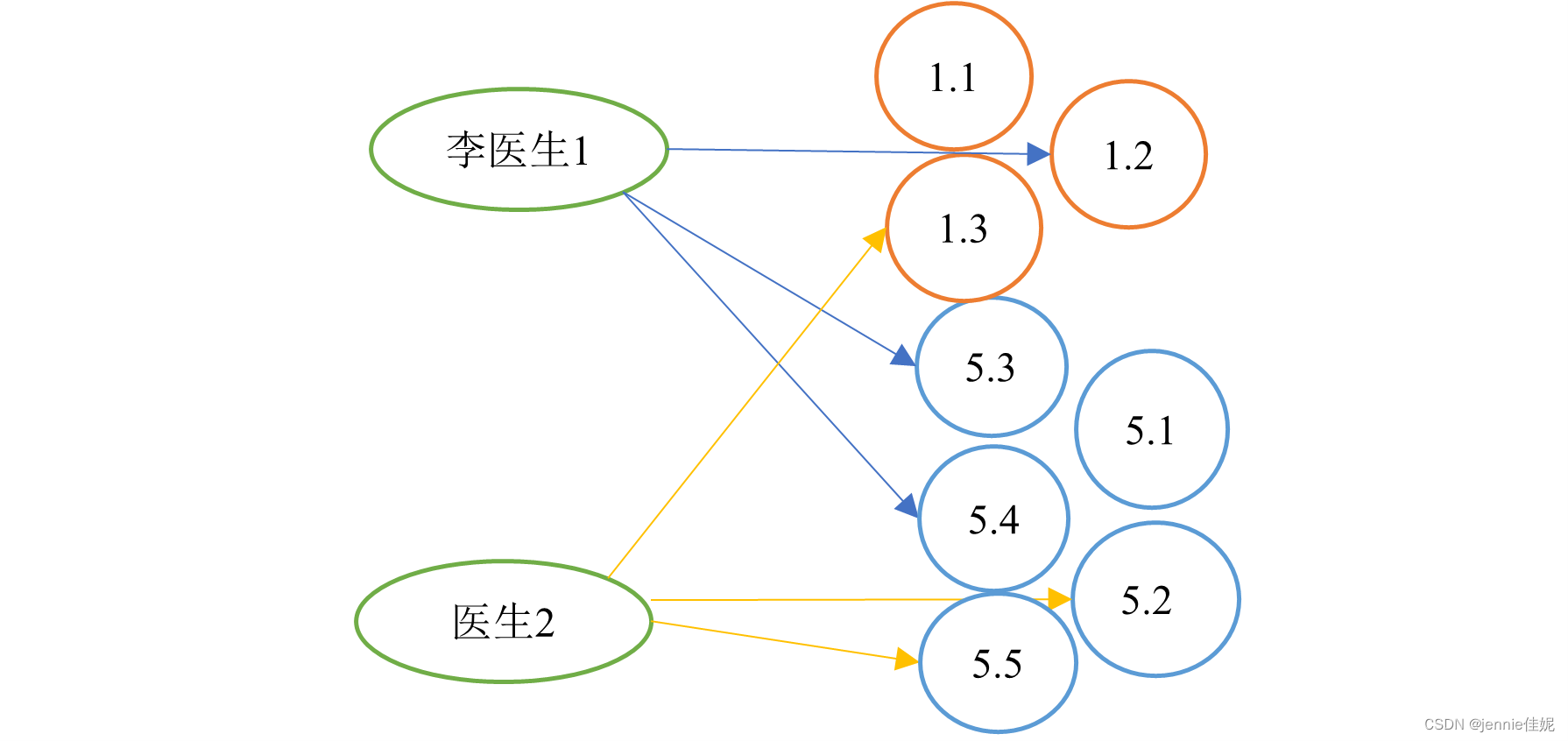
图表 4 流网络生成

流网络最大流——值班问题

答：为了实现题目最后提及的2个要求，我们可以巧用容量限制和增加额外限制节点。

• 每个医生最多只能值班c 个假日：

在本题如果把流量当做医生值班天数，那么意味着流向每个医生的流量限制应该为c。

• 每个医生在一个假期中只能值班1个假日。

那么我们需要先做到保留不同假日对应的假期信息——需要添加假期结点在医生节点和假日结点之间，且医生与假期之间流量限制应该为1。为了保留不同医生与假日的对应关系，所以同一假期对应每个医生都会产生一个假期节点，具体如下：

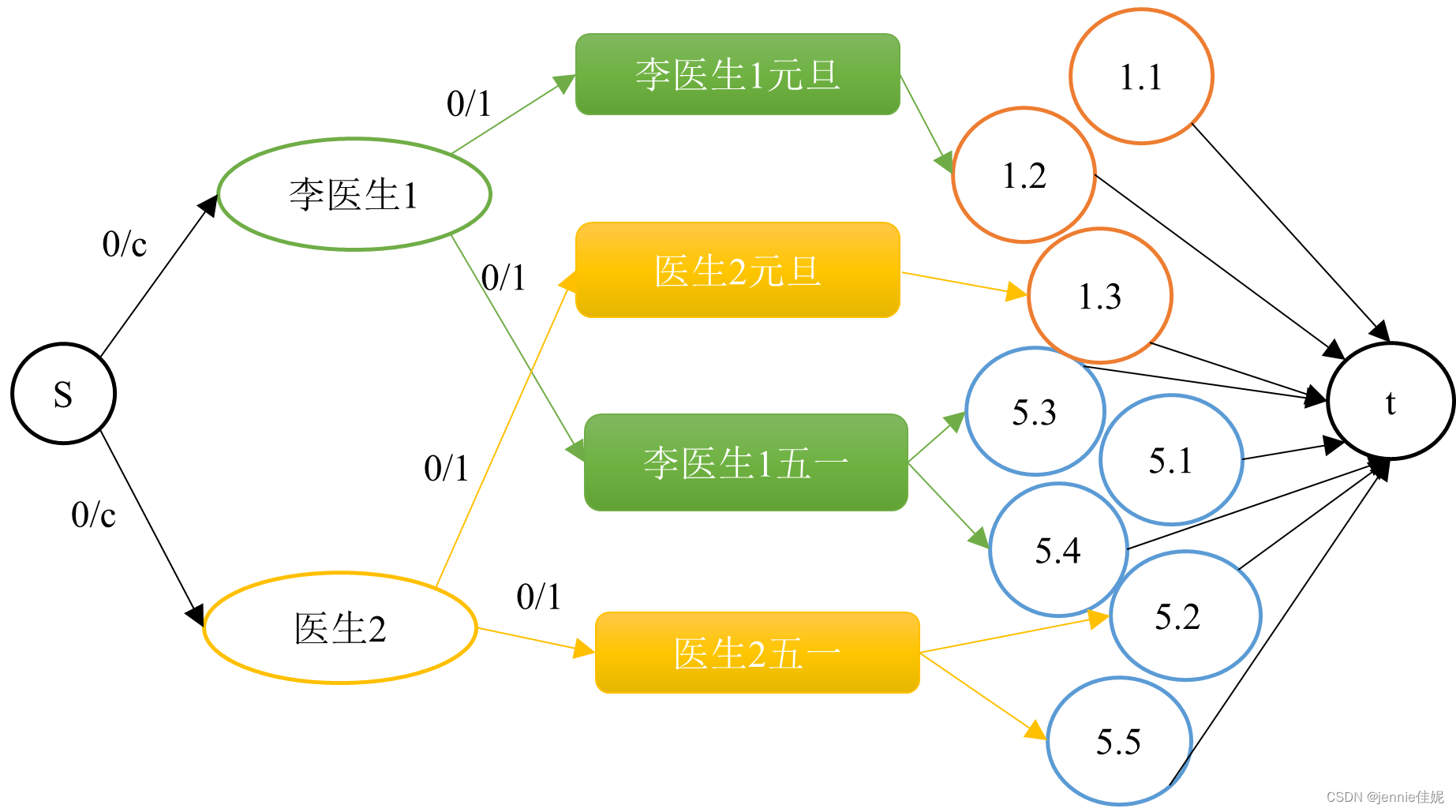
图表 5问题转化为最大流

• 基于生成的数据，计算出排班的方案。

最大流FORD-FULKERSON方法已在原理处说明，在此不再赘述。

FORD-FULKERSON伪代码如下：

While p=findPath():

    RenewMap(p,map)

基于FORD-FULKERSON方法的EDMONDS-KARP算法

它采用广度优先搜索bfs确定当前图的最短增广路径，即节点最少。这样能减少残留网络的更新量。

EDMONDS-KARP算法时间复杂度

设顶点数为n，边数为e，则总共需要n*e次bfs。因为bfs时间复杂度为O(e)，则总时间复杂度为O(n*e*e)。

• 算法优化：DINIC算法（BFS分层dfs）

 

 DINIC伪代码：

dfs(x,minval):    //x为点序号,minval为到达点x的（最小）流
    if x==t:    //到达汇聚节点t返回
    Return paths
for y in x.adj:    //遍历x的下一邻点,进行整一层的更新
    renew(minval)    //更新邻点边加入后（最小）流
    res=dfs(y,minval):
    if res:
        reweight(edge(x,y))
        return res
return 0

while bfs():
    while dfs()

    最坏情况是时间复杂度为O（e*e*n）。

数据处理

重复10次实验取平均值，为了方便统计各个参数我们值取相同。分别以数据规模为10-60。实验结果如下：

Figure 1 运行时间

数据规模	10	20	30	40	50	60
EK	0.045	1.02	5.265	15.703	41.399	102.518
Dinic	0.002	0.024	0.052	0.156	0.369	0.703

Figure 2 算法运行时间

结论：

可以看出随着数据规模的增大，Dinic算法的效率远远高于EDMONDS-KARP算法。

通过本次实验，我掌握了最大流算法思想，了解关于图论中流网络、割、残留网络、残留容量等概念。理解了Ford-Fulkerson算法、EDMONDS-KARP算法、Dinic算法。尝试着运用最大流算法解决关于医生值班的问题。