【机器学习】线性回归（超详细）

最新推荐文章于 2024-09-24 20:25:51 发布

23#.lsy

最新推荐文章于 2024-09-24 20:25:51 发布

阅读量2.2w

点赞数 126

分类专栏：机器学习文章标签：机器学习线性回归人工智能

本文链接：https://blog.csdn.net/weixin_51781852/article/details/122627291

版权

机器学习专栏收录该内容

14 篇文章 53 订阅

订阅专栏

上一篇：机器学习是什么？https://mp.csdn.net/mp_blog/creation/editor/122619296

2.单变量回归

2.1模型表示

我们先从一个例子开始：这个例子是关于预测房屋价格的，我们已知这样一个数据集：

横坐标表示房屋的面积，纵坐标表示房屋的价格。我们的目的是预测当房屋的面积确定时，房屋的价格是多少。比方说，如果你朋友的房子是1250平方尺大小，你通过上图的数据集就可以预测出能卖多少钱，那么，我们具体应该怎么预测呢？

为了便于之后的理解，我们有必要先了解训练集和测试集的概念（相关概念在上一篇中也提到过，也可直接看上一篇中的解释），已经知道的同学可以直接隔过去下一段：

为了测试机器学习算法的效果，通常使用两套独立的样本集：训练集和测试集。当机器学习程序开始运行时，使用训练集作为算法的输入，训练完成之后的那个东西叫模型，我们可以借助模型，通过输入测试集来预测目标变量。比较预测出来的目标变量和实际目标变量之间的差别，就可以算出算法的实际精确度。

你可以做的一件事就是构建一个模型，比如说拟合一条直线，如上图所示，从这个模型上来看，也许你可以告诉你的朋友，他能以大约 220000(美元)左右的价格卖掉这个房子。这就是监督学习算法的一个例子，或者更确切的说这是一个回归问题。

以此例为基础，假使我们上例的训练集如下表所示：

为了将来我们描述这个训练集，我们做了如下的规定：★★★★★

𝑚 代表训练集中实例的数量

𝑥 代表特征/输入变量

𝑦 代表目标变量/输出变量

(𝑥, 𝑦) 代表训练集中的实例

$(x^{(i)},y^{(i)})$ 代表第𝑖 个观察实例

ℎ 代表学习算法的解决方案或函数也称为假设（hypothesis）

ℎ 代表 hypothesis(假设)，ℎ表示一个函数，也是模型，输入是房屋尺寸大小，输出是房屋的价格。

我们需要借助h来预测房价。实际上，我们是要将训练集“喂”给我们的学习算法，进而学习得到一个假设ℎ，然后将我们要预测的房屋的尺寸作为输入变量输入给ℎ，预测出该房屋的交易价格作为输出变量输出为结果。那么，既然h是一个函数，那么它长什么样子呢？

一种可能的表达方式为：ℎ𝜃 (𝑥) = 𝜃0 + 𝜃1𝑥，因为只含有一个输入变量，因此这样的问题叫作单变量线性回归问题。

2.2代价函数

我们用假设函数来表示我们预测结果的模型。那么，这个模型好还是不好呢？我们需要有一个判别标准，这个标准就叫作代价函数。

代价函数： $J(\theta _{0},\theta _{1})=\frac{1}{2m}\Sigma _{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})^{2}$

说一下我对这个公式的理解：通过训练集我们可以得到假设函数h，即我们建立的模型，y是测试集。通过输入测试集的自变量向函数h和y,得出预测出来的结果与实际的结果，让两者相减得到误差，通过误差可以看出我们预测的结果好还是不好，如果误差小于某一个极小数时，我们可以认为我们建立的模型非常成功，反之则是失败。求和的目的是把所有预测值的误差加起来，平方的目的是保证求和的时候，误差是正数，除以m是求平均误差，除以2是为了今后对代价函数求导方便的一种手段。

举个例子：比如说我们有如下的数据集

三个样本点，分别为（1，1），（2，2），（3，3），且已知我们通过训练集，拟合了一条直线方程(假设函数)是： $h=\frac{1}{2}x$ 。

那么:

$J(\Theta _{0},\Theta _{1})=J(0,\frac{1}{2})=\frac{1}{6}\Sigma _{i=1}^{3}(h_{\theta}x^{(i)}-y^{(i)})^{2}=\frac{1}{6}[(\frac{1}{2}-1)^{2}+(1-2)^{2}+(\frac{2}{3}-2)^{2}]=\frac{1}{4}$

如果假设函数是 $h=x$ ,那么易知 $J(0,1)=0$ .通过对比这两个式子可知，当 $J(\theta _{0},\theta _{1})$ 取最小值时，误差最小，假设函数拟合的最好。

即我们的目的变成了，求当 $J(\theta _{0},\theta _{1})$ 取最小值时，将其所对应的参数 $\theta _{1},\theta _{2}$ ，代入ℎ𝜃 (𝑥) = 𝜃0 + 𝜃1𝑥这个式子中即得假设函数。

那么如何求 $J(\theta _{0},\theta _{1})$ 的最小值，变成了我们最主要的问题，解决这个问题的方法有很多，这里我们介绍一种最常用的方法：梯度下降（下文有介绍）

2.2.1代价函数的直观理解I

我们先理解含有一个参数的代价函数。还以上面的那个例子为例，我们来探究：假设函数与代价函数之间有什么关系。

观察如下数据集：

已知：

$h_{\theta }(x)=\theta _{0}+\theta _{1}x$ ,当 $\theta _{0}=0,\theta _{1}=1$ 时， $h_{\theta }(x)=x$ ,由 $J(\theta _{0},\theta _{1})=\frac{1}{2m}\Sigma _{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})^{2}$

可算出 $J(0,1)=0$ ,如下图所示

同理，当 $\theta _{0}=0,\theta _{1}=0.5$ 时可画出如下

同理，当 $\theta _{0}=0,\theta _{1}=0$ 时

由此类推，当 $\theta _{1}$ 取所以取值时， $J(\theta _{1})$ 的图像如下图所示

由图像我们可以知道，当 $J(\theta _{1})$ 取最小值时的参数所对应的假设函数是拟合数据最好的直线。

2.2.2代价函数的直观理解II

那么，再增加一个参数呢？我们知道，有时候我们需要在一大推数据中拟合出来的直线不一定非得过原点，那么这个时候就需要再增加一个参数 $\theta _{0}$ ，那么， $J(\theta _{0},\theta _{1})$ 的图像该怎么表示呢？

多了一个参数相当于多了一个维度，图像也由一开始的二维拓展到了三维。求代价函数的最小值仍然是我们的目标。下面介绍求代价函数最小值的方法：梯度下降

2.3梯度下降

梯度下降的目的：求代价函数的最小值

那么如何更好的理解“梯度下降”呢？其实我们可以把它想象成“下山”的场景。如何从高山上以最快的速度走到山脚呢？那就是：以我们所在的位置为基准，寻找该位置最陡峭的方向，然后沿该方向走一段路程，并且每走一段路程，都要重新寻找当前位置最陡峭的方向，然后沿新的方向再走一段路程，反复采用以上的方法，就能以最快的速度走到山脚下。

在下山的过程中，我们每走一段路，都需要确认新位置最陡峭的方向。如何“确认最陡峭的方向”这个问题最为关键。而“梯度”就可以反映最陡峭的方向。

梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。想要进一步深入了解梯度的可以点击一下

那么具体我们应该怎么做呢？

最核心的思路是：实时更新参数

由上面的内容，我们知道：

$h_{\theta }(x)=\theta _{0}+\theta _{1}x$

$J(\theta _{0},\theta _{1})=\frac{1}{2m}\Sigma _{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})^{2}$

为什么要实时更新参数？我们知道，在下山的过程中，因为我们每走一段路，就要确定新的方向，不断确定新的方向意味着代价函数的参数不断在变化，而我们要想获得新的参数就必须要在已知旧的参数的基础上获得。

我们需要不断重复更新参数的过程是（批量梯度下降）：

$\theta _{j}:=\theta _{j}-\alpha \frac{\varphi }{\varphi \theta _{j}}J(\theta _{0},\theta _{1})$

其中𝑎是学习率（learning rate），它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大，在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。

批量梯度下降的具体实现的步骤如下所示：

接下来我们将更深入的理解这个公式

2.3.1梯度下降的直观理解

$\theta _{j}:=\theta _{j}-\alpha \frac{\varphi }{\varphi \theta _{j}}J(\theta _{0},\theta _{1})$

描述：𝑎是学习率，它决定了我们下山过程中迈出的步子有多大。求导( $\frac{\varphi }{\varphi \theta _{j}}J(\theta )$ )的目的是为了确定下山的方向，等式右面的 $\theta _{j}$ 是旧的参数，左边的 $\theta _{j}$ 是新的参数，每走一步（每一次迭代）我们都需要确定新的参数，因为只有更新了参数才能确定下一步的方向。

需要注意的是：a虽然决定了我们迈出的步子的大小，但是，步子的大小却不仅仅是由a决定的，还与它后面的偏导数有关。 $\frac{\varphi }{\varphi \vartheta _{j}}J(\theta )$ 就是我们前面提到的“梯度”，梯度的本质是一个向量，(有大小，有方向),其大小和a一同决定了迈出步子的大小，其方向决定了“下山”最快的方向。

让我们来看看如果 𝑎 太小或 𝑎 太大会出现什么情况：

如果a太小，即我们下山的步子迈的很小，每次我们只能一点一点的移动，这样导致我们走的很慢，需要很多步才能走到最低点。

如果a太大，那么梯度下降法可能会越过最低点，甚至可能无法收敛，下一次迭代又移动了一大步，越过一次，又越过一次，一次次越过最低点，直到你发现实际上离最低点越来远。就像下图所示：

所以，由此可见，a取一个适当的值是一个多么重要的事情啊。好，现在假设我们取的a值非常的好，那么让我们看看代价函数是怎样一步步地收敛到最小值的。

如下图所示：

先初始化当前所在位置，根据公式计算出梯度下降一步之后的位置，然后再以此位置为基础，让参数值减去学习率乘以该点的导数，得出再梯度下降一步之后的位置，即新的参数值。重复上面的步骤直到走到最低点。在此过程中，我们发现随着梯度下降法的运行，点移动的幅度会越来越小，这是因为，点越往下走，导数的值越小,而a不变，所以步幅会减小。

2.3.2梯度下降的线性回归

接下来我们让梯度下降与线性回归相结合（关键在于对代价函数求偏导）：

如果你之前学过线性代数，你应该知道有一种计算代价函数𝐽最小值的数值解法，不需要梯度下降这种迭代算法。在文章的最后，我们也会谈到这个方法，它可以在不需要多步梯度下降的情况下，也能解出代价函数𝐽的最小值，这是另一种称为正规方程(normal equations)的方法。实际上在数据量较大的情况下，梯度下降法比正规方程要更适用一些。

3.线性代数的回顾

3.1矩阵和向量

矩阵的定义：由m×n个数排成的m行n列数表，称为一个m行n列矩阵，简称m×n矩阵。例如，如图：这是一个3×5矩阵，即3行5列。

怎么表示矩阵里的元素？

$A_{ij}$ 指第i行第j列的元素，例如上图： $A_{22}$ =2

向量是一种特殊的矩阵，即列矩阵，如：

3.2加法和标量乘法

矩阵的加法： 只有当相加的矩阵行数和列数相等时才能相加

例：

标量乘法（矩阵的数乘）：每个元素都要乘

3.3矩阵向量乘法

矩阵和向量的乘法：𝑚 × 𝑛的矩阵乘以𝑛 × 1的向量，得到的是𝑚 × 1的向量

例：

3.4矩阵的乘法

两个矩阵相乘，前提条件是：第一个矩阵的列等于第二个矩阵的行。矩阵相乘的规则为：

例如：

3.5矩阵乘法的性质

矩阵乘法满足下列运算规律：

$1^{0}$ 结合律（AB）C=A(BC);

$2^{0}$ 数乘结合律 k(AB)=(kA)B=A(kB),k为数;

$3^{0}$ 分配律 A(B+C)=AB+AC,(B+C)A=BA+CA.

矩阵的乘法不满足交换律，除了单位矩阵。

单位矩阵：对角元素全为1，其余位置的元素全为0的矩阵。

3.6逆，转置

矩阵的逆：

前面我们定义了矩阵的加法，减法和乘法三种运算。自然的，欲在矩阵中引入类似于除法的概念，其关键在于引入类似于倒数的概念。

对于任意方阵A，有AI=IA=A.所以，从矩阵的乘法角度来看，单位矩阵I类似于数1的作用。一个数a≠0的倒数可用来刻画，类似的，我们引入逆矩阵的概念。

定义设A为n阶方阵，若存在n阶方阵B，使得AB=BA=I,则称A是可逆矩阵，简称A可逆，并称B是A的逆矩阵。

定理1 设A是逆矩阵，则它的逆矩阵是唯一的。

有定义可知，若B是A的逆矩阵，则A亦是B的逆矩阵，它们互为逆矩阵。

若A可逆，则A的逆矩阵存在，记为 $A^{-1}$ ,且 $AA^{-1}=A^{-1}A=I$

矩阵的转置：

把一个矩阵A的行列互换，所得到的矩阵称为A的转置，记为 $A^{T}$ .确切的定义如下

定义设

$A=\begin{pmatrix} a_{11} &a_{12} &... &a_{1n} \\ a_{21} &a_{22} &... &a_{2n} \\ ...&... & ...&... \\ a_{m1}&a_{m2} &... &a_{mn} \end{pmatrix},$

则称

$A^{T}=\begin{pmatrix} a_{11} &a_{21} &... &a_{m1} \\ a_{12}&a_{22} &... &a_{m2} \\ ... &.... &... &... \\ a_{1n}&a_{2n} &... &a_{mn} \end{pmatrix}$

为A的转置。

显然，m×n矩阵的转置是n×m矩阵.

矩阵的转置满足以下规律：

$1^{0}$ $(A^{T})^{T}=A;$

$2^{0}$ $(A+B)^{T}=A^{T}+B^{T};$

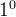
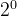
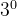
$3^{0}$ $(kA)^{T}=kA^{T},$ k为数

$4^{0}$ $(AB)^{T}=B^{T}A^{T}.$

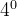
4.多变量线性回归

4.1多维特征

目前为止，我们探讨了单变量线性回归模型，现在我们对房价模型增加更多的特征，例如房间的数量，楼层数和房屋的年龄等，构成一个含有多变量的模型，模型中的特征为（x1,x2,...,xn）。

增添更多特征后，我们引入新的注释：

n 代表特征的数量

$x^{(i)}$ 代表第i个训练实例，表示特征矩阵中的第i行，是一个向量，比如说，上图的

$x^{(2)}=\begin{pmatrix} 1416\\ 3\\ 2\\ 40\\ 232 \end{pmatrix}$

$x_{j}^{(i)}$ 代表特征矩阵中第 𝑖 行的第 𝑗 个特征，也就是第 𝑖 个训练实例的第 𝑗 个特征。

这个时候的假设函数也就相应变成了： $h_{\theta }(x)=\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2}+...+\theta _{n}x_{n}$

这个公式中有n+1个参数和n个变量，为了能够使公式简化一些，引入 $x_{0}=1$ ,则公式转化为： $h_{\theta }(x)=\theta _{0}x_{0}+\theta _{1}x_{1}+\theta _{2}x_{2}+...+\theta _{n}x_{n}$

此时该模型中的参数和变量都是n+1维的向量，可以写成如下的形式：

$\theta =\begin{pmatrix} \theta _{0}\\ \theta _{1}\\ \theta _{2}\\ ...\\ \theta _{n} \end{pmatrix},X=\begin{pmatrix} x_{0}\\ x_{1}\\ x_{2}\\ ...\\ x_{n} \end{pmatrix}$ ,所以 $h_{\theta }(x)=\theta ^{T}X$ ,其中上标T代表矩阵的转置。

4.2多变量梯度下降

与单变量线性回归类似，在多变量线性回归中，我们也构建一个代价函数，和单变量代价函数类似，这个代价函数也是所有建模误差的平方和，即： $J(\theta _{0},\theta _{1}...\theta _{n})=\frac{1}{2m}\Sigma _{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})^{2}$

其中， $h_{\theta }(x)=\theta _{0}x_{0}+\theta _{1}x_{1}+\theta _{2}x_{2}+...+\theta _{n}x_{n}$

我们的目标和单变量线性回归问题中一样，是要找出使得代价函数最小的一系列参数。

多变量线性回归的批量梯度下降算法为：

4.2.1梯度下降法实践1-特征缩放

在我们面对多维特征问题的时候，我们要保证这些特征都具有相近的尺度，这将帮助梯度下降算法更快地收敛。以房价问题为例，假设我们使用两个特征，房屋的尺寸和房间的数量，尺寸的值为 0- 2000 平方英尺，而房间数量的值则是 0-5 ，以两个参数分别为横纵坐标，绘制代价函数的等高线图能，看出图像会显得很扁，梯度下降算法需要非常多次的迭代才能收敛。

解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到 1 之间，如图：

这样迭代的次数会大大降低。那么具体我们应该怎么做呢？

最简单的方法是令： $x_{n}=\frac{x_{n}-u_{n}}{s_{n}}$ ,其中， $u_{n}$ 是平均值， $s_{n}$ 是标准差。

4.2.2梯度下降法实践2-学习率

梯度下降算法收敛所需要的迭代次数根据模型的不同而不同，我们不能提前预知，但是我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。

例如如下的这种，通过观察函数图形，我们知道当参数趋于无穷大时，代价函数的最小值也逐渐趋于一个稳定的值，即收敛。

也有一些自动测试是否收敛的方法，例如将代价函数的变化值与某个阀值（例如 0.001 ）进行比较，当代价函数的最小值小于阈值时，我们也认为是收敛的。但通常看上面这样的图表更好。

梯度下降算法的每次迭代受到学习率的影响，如果学习率 𝑎 过小，则达到收敛所需的迭代次数会非常高；如果学习率𝑎 过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛。

所以我们通常可以考虑尝试这些学习率： 𝛼 = 0.01， 0.03 ， 0.1 ， 0.3 ， 1 ， 3 ，10

4.3特征和多项式回归

如预测房价问题：

如果我们只有房屋所占面积的长度和宽度两个特征变量，那么假设函数应该写成这个样子： $h_{\theta }(x)=\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2}$ 其中， $x_{1}$ 是长度， $x_{2}$ 是宽度。当然了，为了计算方便，我们也可以将假设函数改写成这个样子： $h_{\theta }(x)=\theta _{0}+\theta _{1}X$ ,其中 $X=x_{1}*x_{2}$ ，X是面积。