Leetcode刷题详解——衣橱整理

1. 题目链接：LCR 130. 衣橱整理

2. 题目描述：

家居整理师将待整理衣橱划分为 m x n 的二维矩阵 grid，其中 grid[i][j] 代表一个需要整理的格子。整理师自 grid[0][0] 开始 逐行逐列 地整理每个格子。

整理规则为：在整理过程中，可以选择 向右移动一格 或 向下移动一格，但不能移动到衣柜之外。同时，不需要整理 digit(i) + digit(j) > cnt 的格子，其中 digit(x) 表示数字 x 的各数位之和。

请返回整理师 总共需要整理多少个格子。

示例 1：

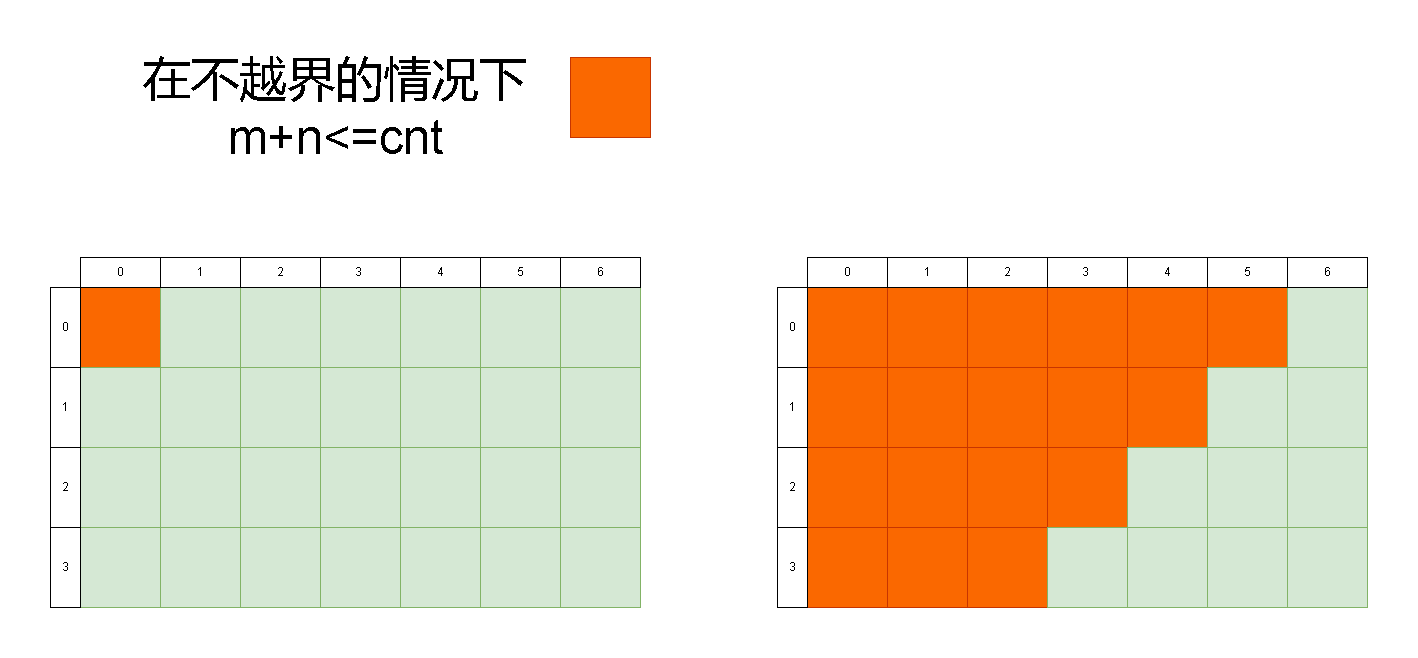
输入：m = 4, n = 7, cnt = 5
输出：18

提示：

• 1 <= n, m <= 100
• 0 <= cnt <= 20

3. 算法思路：

这是一道非常典型的搜索类问题

我们可以通过深搜或者宽搜，从[0,0]点出发，按照题目的规则一直往[m-1,n-1]位置走，

同时设置一个全局变量，每次走到一个合法的位置，就将全局变量加1，当我们把所有走到的路都走完之后，全局变量里存的就是最终答案

4. 算法流程：

1. 定义变量和数组：在类Solution中，定义了以下成员变量和数组：

   • m、n、cnt：分别表示矩阵的行数、列数和计数器。
   • vis：布尔数组，用于记录每个位置是否被访问过。
   • ret：整数变量，用于记录结果。
   • dx和dy：两个整数数组，分别表示上下左右四个方向的偏移量。

2. 函数wardrobeFinishing：这是算法的主函数，接收三个参数：矩阵的行数_m、列数_n和计数器_cnt。它的作用是调用深度优先搜索算法来解决问题，并返回结果。

   • 将参数赋值给成员变量m、n和cnt。
   • 调用dfs(0, 0)从矩阵的第一个位置开始进行深度优先搜索。
   • 返回结果ret。

3. 函数dfs：这是一个递归函数，用于执行深度优先搜索。它接收两个参数：当前位置的行坐标i和列坐标j。

   • 将结果ret加1。
   • 标记当前位置为已访问。
   • 遍历四个方向（上、下、左、右），计算下一个位置的坐标。
   • 如果下一个位置在矩阵范围内且未被访问过且满足条件（通过调用check(x, y)函数判断），则继续递归调用dfs(x, y)进行深度优先搜索。

4. 函数check：这是一个辅助函数，用于检查给定位置是否满足特定条件。它接收两个参数：当前位置的行坐标i和列坐标j。

   • 初始化变量tmp为0，用于存储数字之和。
   • 使用循环，当i不为0时，执行以下操作：
     • 将i的个位数加入tmp。
     • 将i除以10，去掉个位数。
   • 使用循环，当j不为0时，执行以下操作：
     • 将j的个位数加入tmp。
     • 将j除以10，去掉个位数。
   • 判断tmp是否小于等于计数器cnt，如果是则返回true，否则返回false。

这个算法的目的是通过深度优先搜索遍历矩阵中的每个位置，并根据特定条件进行判断和处理。最终的结果存储在变量ret中，并通过函数wardrobeFinishing返回。

5. C++算法代码：

class Solution {
    int m, n, cnt; // 定义变量m、n、cnt，分别表示矩阵的行数、列数和计数器
    bool vis[101][101]; // 定义布尔数组vis，用于记录每个位置是否被访问过
    int ret; // 定义变量ret，用于记录结果
    int dx[4] = {0, 0, 1, -1}; // 定义数组dx，表示上下左右四个方向的偏移量
    int dy[4] = {1, -1, 0, 0}; // 定义数组dy，表示上下左右四个方向的偏移量

public:
    int wardrobeFinishing(int _m, int _n, int _cnt) { // 定义函数wardrobeFinishing，接收三个参数：矩阵的行数、列数和计数器
        m = _m, n = _n, cnt = _cnt; // 将参数赋值给成员变量
        dfs(0, 0); // 从矩阵的第一个位置开始进行深度优先搜索
        return ret; // 返回结果
    }

    void dfs(int i, int j) { // 定义函数dfs，接收两个参数：当前位置的行坐标和列坐标
        ret++; // 结果加1
        vis[i][j] = true; // 标记当前位置为已访问
        for (int k = 0; k < 4; k++) { // 遍历四个方向
            int x = i + dx[k], y = j + dy[k]; // 计算下一个位置的坐标
            if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && check(x, y)) { // 如果下一个位置在矩阵范围内且未被访问过且满足条件
                dfs(x, y); // 继续深度优先搜索
            }
        }
    }

    bool check(int i, int j) { // 定义函数check，接收两个参数：当前位置的行坐标和列坐标
        int tmp = 0; // 定义变量tmp，用于存储数字之和
        while (i) { // 当i不为0时，执行循环
            tmp += i % 10; // 将i的个位数加入tmp
            i /= 10; // i除以10，去掉个位数
        }
        while (j) { // 当j不为0时，执行循环
            tmp += j % 10; // 将j的个位数加入tmp
            j /= 10; // j除以10，去掉个位数
        }
        return tmp <= cnt; // 判断tmp是否小于等于计数器，如果是则返回true，否则返回false
    }
};