《统计软件Stata、SAS及实践》实验报告基础题1

禾六天

已于 2025-04-22 12:40:08 修改

阅读量643

点赞数 22

分类专栏： Stata、SAS 文章标签： Stata SAS

于 2025-04-21 22:41:01 首次发布

本文链接：https://blog.csdn.net/weixin_51936450/article/details/147403244

版权

Stata、SAS 专栏收录该内容

3 篇文章

订阅专栏

一、实验目的及要求

掌握Stata的编程。
掌握SAS的编程方法，包括数据集、循环语句、数组、条件语句、统计图形、回归分析、方差分析等。
要求：通过Stata和SAS编程实现。

二、实验内容、实验步骤及结果

基础题

安装在某种机器上的金属板的平均重量为25千克。对某企业生产的22块金属板进行测量，得到的质量（单位：千克）的数据（B1.xls，见data文件夹）。

实验要求：编写Stata程序，完成并分析以下问题

（1）检验金属板的重量是否服从正态分布；（注：推荐使用Shapiro-Wilk W test，该检验的原假设是样本服从正态分布）

（2）在0.05的显著性水平下，检验该企业生产金属板的重量是否符合要求（注：该检验的原假设是金属板的重量符合要求）。

答：首先，在stata中导入B1.xlsx文件，设置第一行作为变量名。

也可用import语句加路径获取数据。stata程序如下：

. import excel "C:\Users\oo\Desktop\《统计软件Stata、SAS及实践》报告\data\B1.xlsx", sheet("J1") firstrow
(1 var, 22 obs)

（1）本题的原假设为金属板的重量服从正态分布。使用Shapiro-Wilk W test的swilk命令检验，得出W统计量的分布表，可以看到W统计量=0.97426，其对应p值=0.80697 > 0.05，因此接受原假设，即金属板的重量服从正态分布。程序如下及运行结果：

. swilk 重量

                   Shapiro-Wilk W test for normal data

    Variable |        Obs       W           V         z       Prob>z
-------------+------------------------------------------------------
        重量 |         22    0.97426      0.652    -0.867    0.80697

（2）原假设：金属板的重量符合要求，平均重量为25千克。从第（1）小题得出金属板的重量服从正态分布，使用t统计量的ttest命令检验，可以看到t统计量=1.0067，其对应p值=0.3255> 0.05，从而接受原假设，因此在0.05的显著性水平下，可认为该企业生产金属板的重量符合要求。程序如下及运行结果：

. ttest 重量=25

One-sample t test
------------------------------------------------------------------------------
Variable |     Obs        Mean    Std. Err.   Std. Dev.   [95% Conf. Interval]
---------+--------------------------------------------------------------------
    重量 |      22       25.45    .4470078    2.096653     24.5204     26.3796
------------------------------------------------------------------------------
    mean = mean(重量)                                             t =   1.0067
Ho: mean = 25                                    degrees of freedom =       21

    Ha: mean < 25               Ha: mean != 25                 Ha: mean > 25
 Pr(T < t) = 0.8372         Pr(|T| > |t|) = 0.3255          Pr(T > t) = 0.1628

为研究上市公司对其股价波动的关注程度，一家研究机构对在主板，中小板和创业板上市的190家公司进行了调查，得到了信息数据（B2.csv，见data文件夹）。

实验要求：编写Stata程序，完成并分析以下问题

（1）对企业类型绘制饼图，依据关注度进行分类显示，如下图1；

（2）饼图细节设置：扇区1填充红色，分离扇区（选项：特小三分之一）；扇区2填充黄色，不分离扇区；扇区3填充蓝色，不分离扇区。扇区1、2、3的标签都统一设置为百分比。

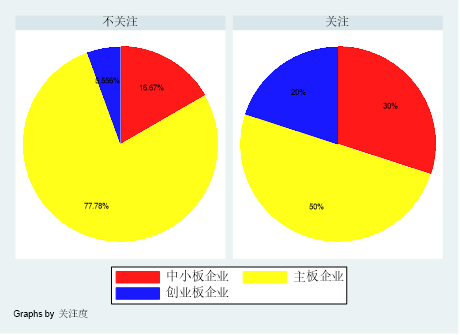
答：①在stata中导入B2.csv文件，设置第一行作为变量名。

. import delimited "C:\Users\oo\Desktop\《统计软件Stata、SAS及实践》报告\data\B2.csv", varnames(1) encoding(UTF-8) clear
(2 vars, 190 obs)

②利用图形工具中的饼图绘制：

③设置类别变量“企业类型”；

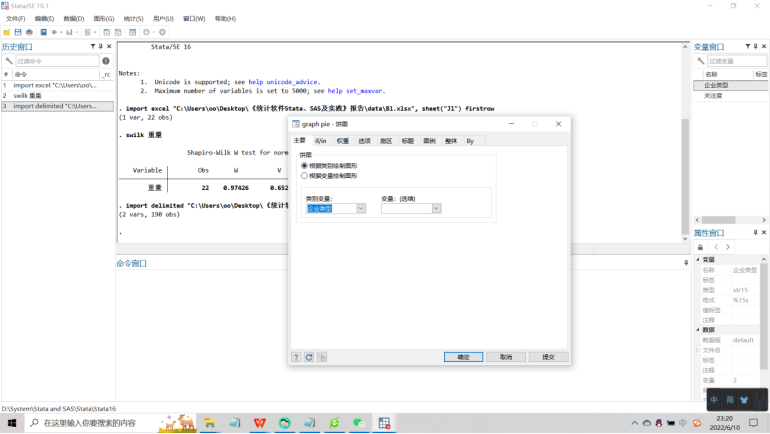
④在扇区属性中设置每个扇区的颜色和分离程度；

⑤在饼图标签属性，设置所有扇区的标签类型为百分比；

⑥按关注度分别绘制饼图；

也可利用绘制饼图的基本命令：graph pie [if] [in] [weight], over (varname) [options]对企业类型绘制饼图。使用options选项中的pie(...)进行饼图的每个扇形外观的细节设置，包括颜色、突出扇形1显示的设定，以及选项plable(...)在所有扇形上百分比的标签设定。最后绘制出和图一一样的饼图。程序如下：

. graph pie, over(企业类型) pie(1, color(red) explode(third_tiny)) pie(2, color(yellow)) pie(3, color(blue)) plabel(_all percent) by(关注度)

下面的每一行数据代表纸箱子的length, width,和height, 单位是厘米。计算每一个箱子的体积、需要的纸板的面积（假定顶部和底部的纸板对折到中间，即：顶部和底部的厚度是两层纸板）。假定纸板的价格为$0.25/平方米。

16 15 24

44 12 32

15 30 45

20 30 36

25 20 40

实验要求：编写SAS程序，完成并分析以下问题

（1）建立一个SAS临时数据集B31读入数据，变量为length，width和 height；

（2）利用数据集B31建立一个新SAS临时数据集B32，它包括B31的所有数据，并建立三个新变量：每个箱子的体积（volume），制造费用（cost），以及每立方米体积的造价y（公式为：y=cost/volume）；

（3）使用建立的数据集B32建立一个新SAS临时数据集B3，只包括其中的volume， cost 和y三个变量。

答：（1）利用数据步创建和管理数据集：建立临时数据集B31读入数据，变量为length，width和 height；利用过程步将结果打印到结果查看器；程序如下：

/* B3(1) */
data B31;					/*创建数据集并命名*/
input length width height;  /*列出数据集的变量名*/
cards;                      
16 15 24
44 12 32
15 30 45
20 30 36
25 20 40
;
run;
proc print data = B31;    /*结果的打印*/
run;

运行结果：

Obs	length	width	height
1	16	15	24
2	44	12	32
3	15	30	45
4	20	30	36
5	25	20	40

（2）通过SET语句复制出数据集B31内的数据建立新的SAS临时数据集B32，它包括B31的所有数据，并建立三个新变量：每个箱子的体积（volume），制造费用（cost），以及每立方米体积的造价y（公式为：y=cost/volume）；程序如下：

/* B3(2) */
data B32;                 /*数据集的创建*/
set B31;                  /* set读取B31的数据，纵向合并数据集,merge(横向)*/
volume = length * width * height;
cost = 0.25 * 0.0001 * (length * width * 4 + length * height * 2 + width * height * 2);
y = cost / volume;
run;
proc print data = B32;   
run;

运行结果：

Obs	length	width	height	volume	cost	y
1	16	15	24	5760	0.06120	.000010625
2	44	12	32	16896	0.14240	.000008428
3	15	30	45	20250	0.14625	.000007222
4	20	30	36	21600	0.15000	.000006944
5	25	20	40	20000	0.14000	.000007000

（3）使用建立的数据集B32建立一个新SAS临时数据集B3，保留其中的volume， cost 和y三个变量，删除length，width和height三个变量。

程序如下：

/* B3(3) */
/* 方法一 keep语句保留变量 */
data B3;                  
set B32(keep = volume cost y);
run;
proc print data = B3;     
run;
/* 方法二 drop语句删除变量 */
data B3;                  
set B32(drop = length width height);
run;
proc print data = B3;     
run;

运行结果：

Obs	volume	cost	y
1	5760	0.06120	.000010625
2	16896	0.14240	.000008428
3	20250	0.14625	.000007222
4	21600	0.15000	.000006944
5	20000	0.14000	.000007000