LeetCode 热题 100—— 二叉树的直径(二叉树）+ 二叉树的层序遍历（二叉树）

目录

543. 二叉树的直径 简单

102. 二叉树的层序遍历 中等

---

简单

给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

示例 1：

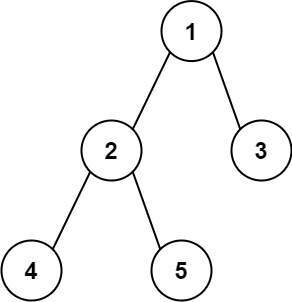
输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

示例 2：

输入：root = [1,2]
输出：1

提示：

• 树中节点数目在范围 [1, 104] 内

• -100 <= Node.val <= 100

//方法一：深度优先搜索
​
/*
最后的算法流程为：我们定义一个递归函数 depth(node) 计算 dnode，函数返回该节点为根的子树的深度。先递归调用左儿子和右儿子求得它们为根的子树的深度 L 和 R ，则该节点为根的子树的深度即为max(L,R)+1。该节点的 dnode值为L+R+1。
递归搜索每个节点并设一个全局变量 ans 记录 dnode 的最大值，最后返回 ans-1 即为树的直径。
*/
​
//时间复杂度：O(N)，其中 N 为二叉树的节点数，即遍历一棵二叉树的时间复杂度，每个结点只被访问一次。
//空间复杂度：O(Height)，其中 Height 为二叉树的高度。由于递归函数在递归过程中需要为每一层递归函数分配栈空间，所以这里需要额外的空间且该空间取决于递归的深度，而递归的深度显然为二叉树的高度，并且每次递归调用的函数里又只用了常数个变量，所以所需空间复杂度为 O(Height) 。
​
class Solution {
    int ans;
    // 计算以 rt 为根的子树的深度（节点数）
    int depth(TreeNode* rt){
        if (rt == NULL) {
            return 0; // 访问到空节点了，返回0
        }
        int L = depth(rt->left); // 左儿子为根的子树的深度（节点数目）
        int R = depth(rt->right); // 右儿子为根的子树的深度
        
        // 更新全局变量 ans：记录当前最长路径的节点数
        ans = max(ans, L + R + 1);
        
        // 返回以当前节点为根的子树的最大深度 用于计算下一个节点
        return max(L, R) + 1; 
    }
public:
    int diameterOfBinaryTree(TreeNode* root) {
        // 初始化最长路径的节点数为1（单节点树的直径为0）
        ans = 1;
        depth(root);
        // 将节点数转换为边数（直径 = 节点数 - 1）
        return ans - 1;
    }
};

102. 二叉树的层序遍历 中等

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1：

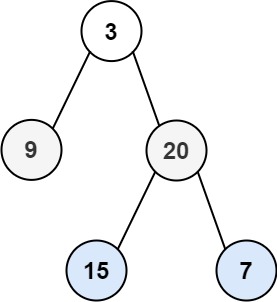
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目在范围 [0, 2000] 内

• -1000 <= Node.val <= 1000

//广度优先搜索
​
​
//时间复杂度：每个点进队出队各一次，故渐进时间复杂度为 O(n)。
//空间复杂度：队列中元素的个数不超过 n 个，故渐进空间复杂度为 O(n)
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> ret;  // 存储最终结果的二维数组
        if (!root) {              // 处理空树的情况
            return ret;
        }
​
        queue<TreeNode*> q;       // 创建队列用于BFS
        q.push(root);             // 根节点入队
        
        while (!q.empty()) {      // 当队列不为空时循环
            int currentLevelSize = q.size();  // 当前层的节点数量
            ret.push_back(vector<int>());     // 为当前层创建空数组
            
            // 只遍历当前层的所有节点
            for (int i = 1; i <= currentLevelSize; ++i) {
                auto node = q.front(); q.pop();  // 队首节点出队
                ret.back().push_back(node->val); // 将节点值加入当前层的数组
                
                // 将子节点（如果存在）入队，为下一层遍历做准备
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
        }
        
        return ret;  // 返回二维数组，每一行代表一层的节点值
    }
};

• ret.push_back(vector<int>()) 这行代码的作用是在二维向量 ret 的末尾添加一个新的空的一维向量。具体来说，它执行了以下操作：

  1. vector<int>()：创建一个空的整数向量（一维数组）。

  2. ret.push_back(...)：将这个空的一维向量添加到 ret 的末尾。

• ret.back() 是一个用于访问容器（如 vector）中最后一个元素的方法。具体到你提供的代码中，ret 是一个存储 vector<int> 的二维数组，ret.back() 表示当前二维数组的最后一行（即当前正在处理的层）。