经典问题 小白鼠试毒药 这个算法你绝对不知道

问题

有1000瓶液体，其中1瓶是毒药，其余的都是水，小白鼠喝了之后一个小时才会生效，问怎样用较少的时间和较少的小白鼠找出这瓶毒药呢？

1000个小白鼠，1个小时？或者1只小白鼠，1000个小时？显然都不是

有一个直观的办法，假如有9个小白鼠，我们把1000瓶药分为10份，每只小白鼠吃一份，这样一次过后就可以把范围缩小到100瓶药，继续实验

但以上均不是最优的办法，其实只需要10只小白鼠，1个小时就可以了！

下面看讲解：

我们可以利用二进制很好地解决这个问题！
首先我们给1000瓶药按999，998，997，996…，3，2，1，0编好号，看了下图就差不多明白了

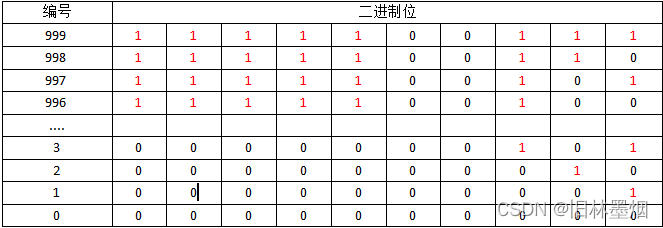
999对应的二进制位就是10位，为什么需要10只小白鼠正是这么来的，我们让这些小白鼠分别对应一位二进制位，假如对应的二进制位值为1，就让小白鼠喝下该瓶液体
比如：
第一只小白鼠喝下编号为999、998、997、996…的液体
第二只小白鼠喝下编号为999、998、997、996…的液体
第三只小白鼠喝下编号为999、998、997、996…的液体
第四只小白鼠喝下编号为999、998、997、996…的液体
第五只小白鼠喝下编号为999、998、997、996…的液体
第六只小白鼠喝下编号为…的液体
第七只小白鼠喝下编号为…的液体
第八只小白鼠喝下编号为999、998、997、996…3的液体
第九只小白鼠喝下编号为999、998…2的液体
第十只小白鼠喝下编号为999、997…3、1的液体

那么死掉的老鼠代表的二进制位就是1，没死掉的就代表0！
假如有毒的液体编号是3，那么第八只和第十只老鼠死了。
反过来，第八只和第十只老鼠死了，我们也可以推出有毒的液体编号是3。

再用一个结果举个例子，假如第八、九、十只老鼠死了，那么代表的二进制为0000000111，可以推出有毒的液体编号是7

是不是很神奇呢！等等！这个问题还没有解决呢！

进阶知识

请读者先理解好上面的讲解再继续看下去哈，防止懵逼！

那么问题来了，上面解读的是1次实验，10只小白鼠，那么假如进行两次实验，至少需要多少只小白鼠呢？答案是七只

两次实验，问题又来了!二进制不能用，那么用三进制！

同样地，我们给1000瓶药按999，998，997，996…，3，2，1，0编好号

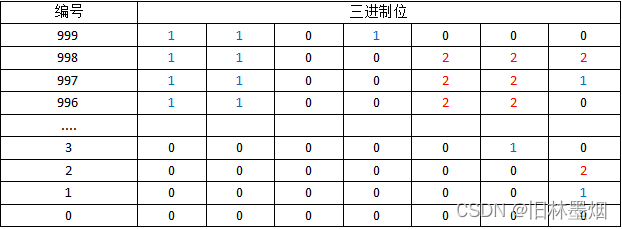
第一次实验
我们的目的是确定进制位值为2的位，假如对应的二进制位值为2，就让小白鼠喝下该瓶液体

比如：
第一只小白鼠喝下编号为…的液体
第二只小白鼠喝下编号为…的液体
第三只小白鼠喝下编号为…的液体
第四只小白鼠喝下编号为…的液体
第五只小白鼠喝下编号为998、997、996…的液体
第六只小白鼠喝下编号为998、997、996…的液体
第七只小白鼠喝下编号为998、2…的液体

哪只小白鼠死掉了就代表对应位三进制的值为2

第二次实验
我们的目的是确定进制位值为1的位，假如对应的二进制位值为1，就让小白鼠喝下该瓶液体

同样的道理，哪只小白鼠死掉了就代表对应位三进制的值为1

进制位值为2、1的都测出来了，0的就没必要测了；

举个例子，6、7号小白鼠第一天死了，3、4号小白鼠第二天死了，那么毒药三进制表示为0011022，可以推出有毒的液体编号是116

当然了，三次实验的就要用四进制了，每次实验就验证一个四进制值就可以了，小白鼠的数量就是进制的最大位数啦！

知识总结

根据以上解读，知道小白鼠数量和实验次数的关系了吧！
小白鼠数量=液体的瓶数转换为实验次数+1进制的最大位数

计算公式就是：
小白鼠数量=[$lo{g}_{实验次数+1}液体数量$]
[]是向下取整的意思

小疑惑：
1、实验过程中小白鼠死掉会影响后面的实验吗？
不会的，小白鼠死掉了，那么其代表的进制位的值已经知道了

2、这是最优的解法吗？
以目前的知识证明，是的，感兴趣可以自行去了解香农熵