每日论文解读（day4）：Tristable property and the high stiffness analysis of Kresling pattern origami [1]

本文链接：https://blog.csdn.net/weixin_52241563/article/details/146045751

首先非常感谢大哥的付出和贡献，该论文于2023年3月发表在IJMS。

先说结论：本文主要描述了对“Kresling”折纸结构的新发现和研究。简单来说，之前我们认为Kresling折纸只有两种能稳定保持的形态（即双稳态），但经过该文的理论推导和实际的折叠实验后，我们发现它实际上可以稳定地保持三种不同的形态（也就是三稳态性）。

接下来介绍Kresling折纸的几何构型部分，因为本节旨在建立一个统一的几何描述标准，分别是三角化圆柱形折纸和三角化圆锥形折纸，所以这里将会详细描述其几何基本构型。

fig.1 Kresling折纸的几何形状 [1]

1、三角化圆柱形折纸

1.1 基本构型与参数

基本结构
圆柱形折纸由重复的三角形阵列组成，每个单元包含一个谷折痕和一个山折痕。图1(a)展示了平板状态的折痕图样，而图1(b)则描述了折叠过程。
主要参数
- n：底面多边形的边数。
- a：底（或顶）多边形的边长。
- α 和 β：定义折纸折叠过程中各折痕比例的两个关键角度。

1.2 折叠状态下的折痕长度

在平面状态经过折叠后，单元内各条折痕的设计长度由下式给出：

1.3 折叠运动的描述

折叠过程采用三个变量来描述：

高度 h：顶面与底面之间的垂直距离。
扭转角 ϕ：描述折叠过程中顶面和底面多边形相对旋转的角度。
半径 R：底面（或外接圆）的半径。

为了计算折叠过程中的折痕实际长度，构建了如下坐标系并定义单元内四个顶点的位置：

通过欧式距离公式得到各折痕的实际长度：

2、三角化圆锥形折纸

2.1 基本构型与参数

圆锥形折纸与圆柱形相似，但在几何描述上引入了以下额外参数：

m：表示顶面多边形与底面多边形边长的比例，满足 0<m<1。当 m=1 时，结构变为圆柱形。

此外，基本参数包括：

n：侧边数。
a：底面多边形的边长。
α 和 β：定义折痕比例的角度。

2.2 折叠状态下的折痕长度

圆锥形折纸在折叠态下的各折痕长度由以下公式给出：

2.3 折叠运动的描述

折叠运动的描述需要考虑顶面和底面两个多边形的外接圆半径：

底面半径为 R
顶面半径为 r（由比例 m 确定）

同样地，构建单元内顶点的坐标：

因此，折痕的实际长度为：

3、两种结构之间的转换

圆锥形折纸相比于圆柱形多了参数 m 和 r。其中，r 与 m 有关，满足当 m=1 时，r=R（即变为圆柱形）。

在实际折叠过程中，一般选取第二稳定态（此处对于圆锥形折纸）作为参考。在图1(c)中，此时认为，折痕 AD 与 BD 的实际长度分别等于设计大小 $L_{AD}$ 和 $L_{BD}$ ，根据这一假设，我们可得：

联立方程，解得第二稳定态下的扭转角 $\phi_0$ 以及满足余弦函数的取值范围：

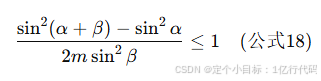
最终得到参数 m 的取值范围：

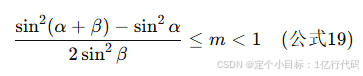
4、总结

论文其他内容将在下面以总结的形式展开，论文之中有以下几点值得我们学习和借鉴：

1）几何描述与统一标准
论文首先建立了一个统一的几何描述标准，将三角化的圆柱形折纸（cylindrical origami）和锥形折纸（conical origami）统一起来研究。作者详细推导了两种结构的基本几何参数（侧边数、底边长度、角度等）以及折叠过程中的主要变量（高度、扭转角、半径等），这为后续动力学和能量分析奠定了基础。

2）发现与验证三稳态特性
传统上，Kresling 折纸被认为只具备双稳态特性，然而该论文通过理论分析和实际折叠试验发现，该结构在折叠过程中实际上存在三个稳定状态。第三稳定状态的出现主要归因于折痕线（特别是谷折痕 BD）的弧形化及整体单元的外弯行为。论文中利用理论模型详细描述了折痕线由直线变为弧线的过程，从而解释了第三稳定状态的形成机制。

3）改进的桁架模型

针对传统桁架模型在描述折纸结构能量变化时的不足，论文提出了修正的桁架模型。主要区别有：

在第一阶段（从平面状态到第二稳定状态），直接利用折痕线的直线距离来计算能量变化；
在第二阶段（从第二稳定状态到第三稳定状态），则引入了折痕线弧形长度的计算，将其作为变形的度量，从而更准确地反映实际结构中的能量跃迁和非线性恢复力。
这种模型的改进不仅可以使能量表观展现出明显的能量跃变，还验证了第三稳定状态的高刚性的特性。

4）能量表观与动态响应分析
论文通过非维化处理，得到了折纸结构在不同折叠状态下的能量表观。能量分析显示，在折叠过程中存在突变点，这一点与第二和第三稳定状态之间的转换密切相关。研究揭示，当折纸结构进入第三稳定状态时，由于谷折痕的弧形化和单元整体外弯，会产生显著的非线性恢复力，从而使得该状态具有极高的刚性和载荷承受能力。

5、引用

[1] Xiaolei Wang et al., ‘Tristable Property and the High Stiffness Analysis of Kresling Pattern Origami’, International Journal of Mechanical Sciences, 256 (2023), p. 108515, doi:10.1016/j.ijmecsci.2023.108515.

解读不能代替原文，好的论文需要您细细品读。