高级数据结构——图

图

图的概念介绍

图是由顶点和边组合.一般我们会以V来定义图的顶点集合(Vertex),以E来定义图的边集合(Edge).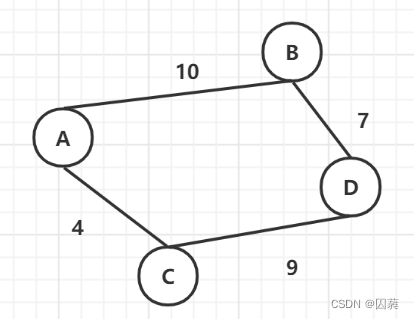

如图,上述即为一个简单的无向图,其中顶点与顶点之间的边上的数值代表该边的权重.
按照是否有方向可以将一个图分为无向图和有向图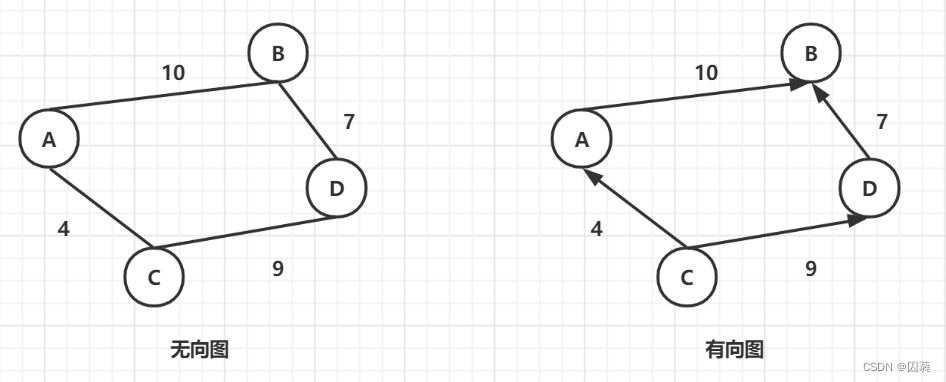

图的存储结构

图的存储结构有两种,分别是邻接表和邻接矩阵.

邻接表

邻接表就是一个链表,链表中每个节点包含4部分:起始顶点,终止顶点,边的权重以及指向下一个节点的指针域.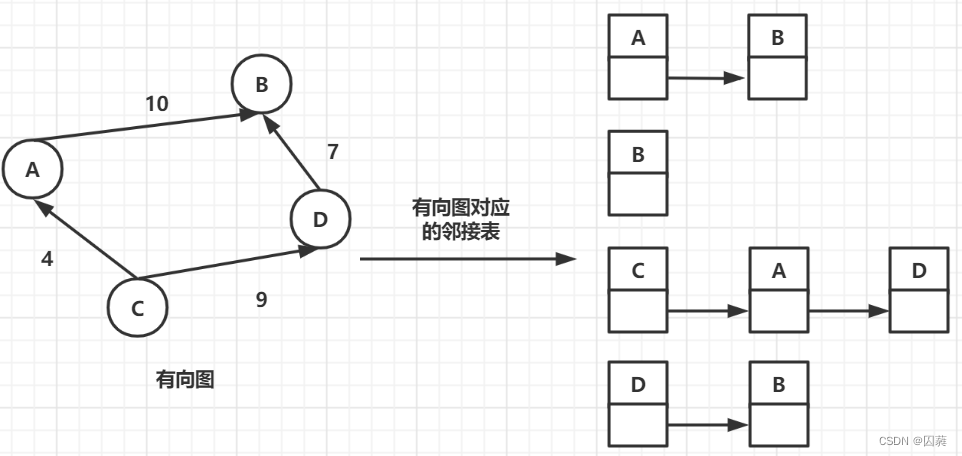
邻接表中每个顶点之后指向的节点都是以该节点作为起始顶点的边的终止顶点.

	// 当两个顶点的边没有设置权重时默认是INF.
	 public static final int INF = Integer.MAX_VALUE;
	// 图的顶点集
    public  char[] V;
	// 邻接表
    public ArrayList<Node> edgeList;
	// 标记图的类型:有向图/无向图
    public boolean isDirect;
    // 邻接表中的节点
    static class Node{
        public int src;
        public int dest;
        public int weight;
        public Node next;
        public Node(int src,int dest,int weight){
            this.src = src;
            this.dest = dest;
            this.weight = weight;
        }
    }
    // 向邻接表中添加节点
	 private void addEdgeChild(int src,int dest,int weight){
	        Node cur = edgeList.get(src);
	        while(cur != null){
	            if(cur.dest == dest){
	                return;
	            }
	            cur = cur.next;
	        }
	        // 头插法插入节点
	        Node node = new Node(src,dest,weight);
	        node.next = edgeList.get(src);
	        edgeList.set(src,node);
	    }

邻接矩阵

邻接矩阵就是一个二维矩阵matrix,其中matrix[i][j]表示顶点i到顶点j的边的权重.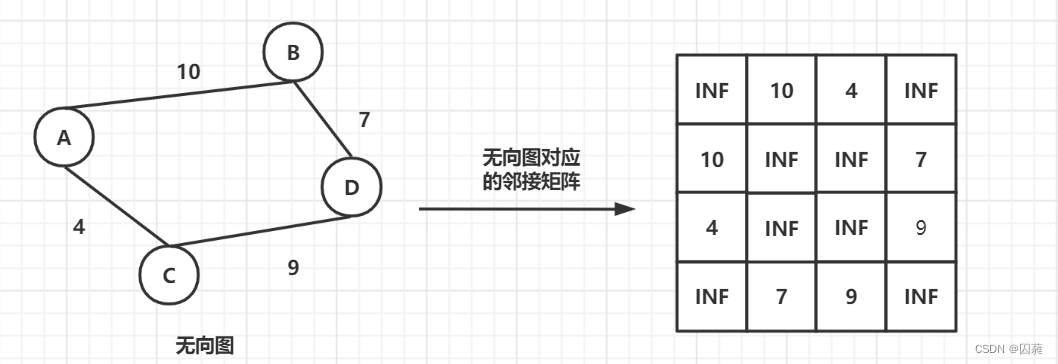
对于无向图而言,其邻接矩阵是一个对称矩阵.

	// 边权重默认为INF
	private static final int INF = Integer.MAX_VALUE;
	// 顶点集
    private char[] V;
    // 邻接矩阵
    private int[][] matrix;
    // 图的类型:有向图/无向图
    private boolean isDirect;
	
	// 邻接矩阵初始化
    public GraphByMatrix(int size, boolean isDirect) {
        V = new char[size];
        matrix = new int[size][size];
        for (int i = 0; i < size; i++) {
            Arrays.fill(matrix[i], INF);
        }
        this.isDirect = isDirect;
    }
	// 初始化顶点集
    public void initV(char[] arr) {
        for (int i = 0; i < arr.length; i++) {
            V[i] = arr[i];
        }
    }
	// 向临界矩阵中添加元素
    public void addEdge(char srcV, char destV, int weight) {
        int srcIndex = getIndexOfV(srcV);
        int destIndex = getIndexOfV(destV);
        if (srcIndex == -1 || destIndex == -1) {
            throw new IndexOutOfBoundsException("不存在这样的顶点");
        }
        matrix[srcIndex][destIndex] = weight;
        if (!isDirect) {
            matrix[destIndex][srcIndex] = weight;
        }
    }
	// 获取某个顶点对应的下标
    private int getIndexOfV(char v) {
        for (int i = 0; i < V.length; i++) {
            if (V[i] == v) {
                return i;
            }
        }
        return -1;
    }

图的遍历

本次介绍以邻接矩阵作为图的存储结构
图的遍历方式分为2种:深度优先遍历(dfs)和广度优先遍历(bfs).

深度优先遍历

深度优先遍历的含义是从图中的一个顶点出发,寻找以其作为起始顶点的边E1,然后输出边E1,之后再以边E1的中止顶点为新的起始顶点递归遍历.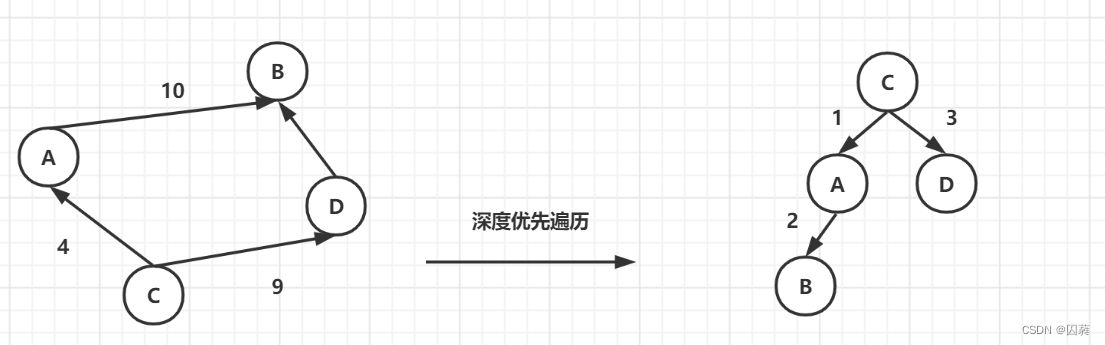

	// 深度优先遍历一般都是采用递归
	public void dfs(char v){
        boolean[] isV = new boolean[V.length];
        int index= getIndexOfV(v);
        dfs(index,isV);
    }
    private void dfs(int index,boolean[] isV){
        System.out.println(V[index] + " ->");
        isV[index] = true;

        for(int i = 0; i < V.length; i++){
            if(matrix[index][i] != INF && !isV[i]){
                dfs(i,isV);
            }
        }
    }

广度优先遍历

广度优先遍历是从图中的一个顶点出发,将所有以其作为起始顶点的边找完后,再以别的顶点为起始顶点去寻找.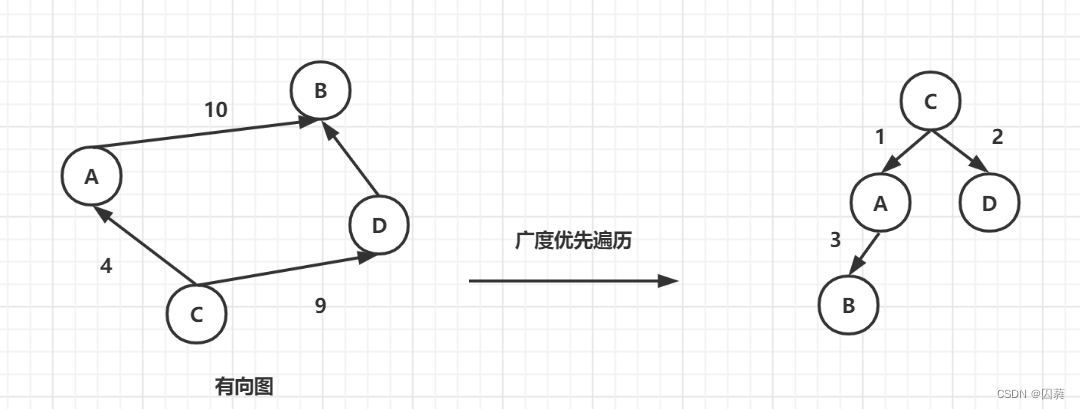

	// 广度优先遍历一般用队列作为载体实现
    public void bfs(char v) {
        boolean[] isV = new boolean[V.length];
        Queue<Integer> q = new LinkedList<>();
        int index = getIndexOfV(v);
        q.offer(index);
        isV[index] = true;
        while(!q.isEmpty()){
            int size = q.size();
            while(size != 0){
                int cur = q.poll();
                System.out.print(V[cur]+" ->");
                for(int i = 0; i < V.length; i++){
                    if(!isV[i] && matrix[cur][i] != INF){
                        isV[i] = true;
                        q.offer(i);
                    }
                }
                size--;
            }
        }
    }

最小生成树

生成树是一个无向连通图的子图,其含义是用尽可能少的边将图中的所有顶点连接起来.在生成树中,从任意一个顶点出发能够访问到图上的任意一个顶点.而最小意味着选取的边的权重和最小.
因此最小生成树就是一棵边权值和最小的生成树.
实现最小生成树的算法有2个,分别是Kruskal算法和Prime算法.

Kruskal算法

Kruskal算法采用的是全局贪心的思想.在一个无向连通子图中,首先选取边权重最小的边,然后把该边的起始顶点和终止顶点利用并查集进行合并,接着在剩下的边中选取边权重最小的边,然后重复上述操作,直到选择了V-1条边(其中V是该无向连通子图的顶点的个数)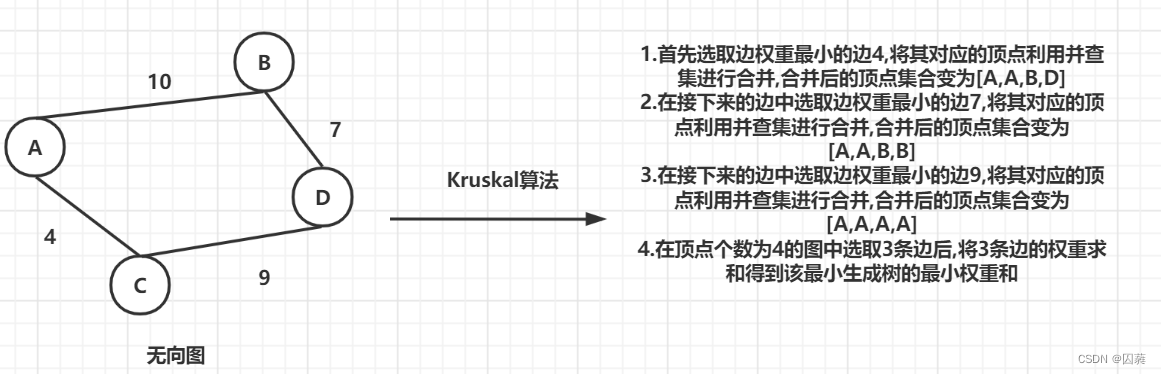

	public int kruskal(GraphByMatrix minTree){
		// 首先将邻接矩阵中的边的权重存放到最小堆中,便于每次取出权重最小的边
        PriorityQueue<Edge> p = new PriorityQueue<>();
        // 初始化最小堆
        for(int i = 0;i < matrix.length; i++){
            for(int j = i + 1; j < matrix.length; j++){
                if(matrix[i][j] != INF){
                    Edge e = new Edge(i,j,matrix[i][j]);
                    p.offer(e);
                }
            }
        }
        // 用并查集判断是否构成回路
        UnionFindSet ufs = new UnionFindSet(V.length);
        // 记录选取的边的个数
        int cnt = 0;
        // 记录最小生成树对应的最小权重和
        int total = 0;
        while(cnt != V.length-1 && !p.isEmpty()){
            Edge e = p.poll();
            // 如果当前边对应的起始顶点和终止顶点已经进行了合并则不再选取该边
            if(ufs.isSameUnion(e.srcIndex,e.destIndex)){
                continue;
            }
            
            minTree.matrix[e.srcIndex][e.destIndex] = e.weight;
            minTree.matrix[e.destIndex][e.srcIndex] = e.weight;
            // 对选取的边的两个顶点进行合并
            ufs.union(e.srcIndex,e.destIndex);
            System.out.println("选择的边" + V[e.srcIndex] + "->" + V[e.destIndex] + ":"+e.weight);
            // 更新最小权重和的值
            total += e.weight;
            cnt++;
        }
        // 如果cnt != V.length-1说明该图本身就不是一个无向连通子图,也就谈不上什么最小生成树了
        return cnt == V.length - 1 ? total : -1;
    }

Prime算法

相比于Kruskal算法而言,Prime算法采用的是局部贪心的思想,即从无向连通子图中随机选取1个顶点A,然后从以该顶点A作为起始顶点的边中选取1个边权重最小的边.之后以边的终止顶点B为起始顶点,再在以顶点A为起始顶点的所有边中和在以顶点B为起始顶点的所有边中选取一个边权重最小的边,重复这个过程直到得到V-1条边(V为该图的顶点个数)

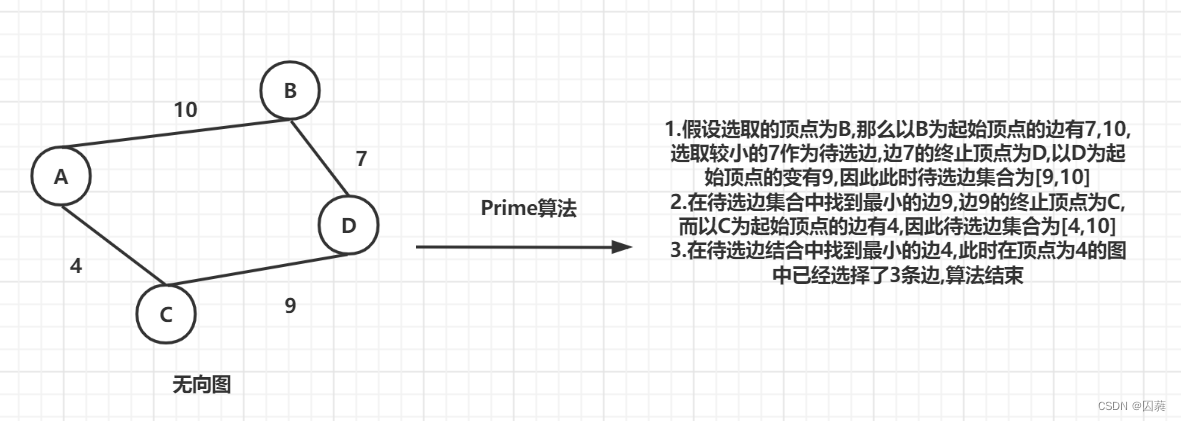
  public int prime(GraphByMatrix minTree,char v){
  		// 首先获取顶点v的下标
        int srcIndex = getIndexOfV(v);
        // 存储选取的边集合
        Set<Integer> setX = new HashSet<>();
        setX.add(srcIndex);
        // 利用最小堆作为待选边集合,便于每次选取边权重最小的边
        PriorityQueue<Edge> p = new PriorityQueue<>();
        // 初始化最小堆
        for(int i = 0; i < V.length; i++){
            if(matrix[srcIndex][i] != INF){
                p.offer(new Edge(srcIndex,i,matrix[srcIndex][i]));
            }
        }
        // 记录选取的边的个数
        int size = 0;
        // 记录最小权重和
        int total = 0;
        while(!p.isEmpty()){
        	// 从待选边集合中选取边权重最小的边
            Edge e = p.poll();
            int src = e.srcIndex;
            int dest = e.destIndex;
            int weight = e.weight;
            if(setX.contains(dest)){
                return -1;
            }else{
            	// 更新最小生成树
                minTree.matrix[src][dest] = weight;
                minTree.matrix[dest][src] = weight;
                size++;
                total += weight;
                setX.add(dest);
                if(size == V.length-1){
                    return total;
                }
            }
            // 以选取的边的终止顶点作为起始顶点,将其没有被选择过的边添加到待选边集合中
            for(int i = 0; i < V.length; i++){
                if(matrix[dest][i] != INF && !setX.contains(i)){
                    p.offer(new Edge(dest,i,matrix[dest][i]));
                }
            }
        }
        return -1;
    }

最短路径

最短路径问题是一个常见的问题.它指的是在从出发点到终点存在多条可达路径的情况下,如何选择一条权重和最小的路径.
最短路径问题分为单源最短路径和多源最短路径,其中单源最短路径是指定了出发点,而多源最短路径则可以实现任意两个顶点之间的最短路径
单源最短路径中常见的算法有Dijkstra算法,Bellman-Ford算法,多源最短路径中常见的算法有Floyd-WarShall算法

Dijkstra算法

Dijkstra算法适用于正向权重的有向图求单源最短路径,无法解决权值为负值的路径问题.
Dijkstra算法也是采用了贪心的思想:即每次都从当前距离出发点距离最短的顶点开始遍历.
首先维护一个dist[]数组和pPath[]数组,其中dist[i]表示从出发点到i点的最短距离,pPath[i]表示从出发点到i点的最短路径中i点的上一个顶点.
假设出发点对应的下边为src,那么初始化dist[i]为INF,dist[src]为0.首先从出发点开始将其能到达的顶点i对应的dist[i]的大小从INF设置为martix[src][i] + dist[src],然后再遍历所有的dist[i],选取没有遍历过且最小的下标i作为起始下标对dist数组进行最短距离的更新,直到所有顶点都被更新过.

 	// dist[i]表示出发点到顶点i的最小距离,pPath[i]表示出发点到顶点i的最短路径中距离顶点i最近的上一个顶点对应的下标
 public void dijkstra(char src,int[] dist,int[] pPath){
 		// 获取出发点对应的下标
        int srcIndex = getIndexOfV(src);
        // 初始化dist数组为INF
        Arrays.fill(dist,INF);
        // 出发点对应的最短距离设置位0
        dist[srcIndex] = 0;
        Arrays.fill(pPath,-1);
        dist[srcIndex] = 0;
        int n = V.length;
        // 标记每个节点是否被访问过
        boolean[] s = new boolean[n];
		
		// 对节点进行遍历
        for(int k = 0; k < n; k++){
            int u = srcIndex;
            int min = INF;
            // 选择未访问过的节点中dist[i]最小的下标i作为起始顶点u
            for(int i = 0; i < n; i++){
                if(!s[i] && dist[i] < min){
                    min = dist[i];
                    u = i;
                }
            }
            // u对应的顶点在这一次遍历中已经访问过了
            s[u] = true;
			// 以u为顶点,对dist数组的其他下标进行最短距离的更新
            for(int v = 0; v < n; v++){
                if(!s[v] && matrix[u][v] != INF && dist[u] + matrix[u][v] < dist[v]){			
                	// 更新dist数组
                    dist[v] = dist[u] + matrix[u][v];
                    // 更新pPath数组
                    pPath[v] = u;
                }
            }
        }
    }

Bellman-Ford算法

Bellman-Ford算法可以解决路径权重为负值的路径问题,但相较于Dijkstra算法的O(n^2) 而言,Bellman-Ford算法的时间复杂度为O(n^3) .
当一个图中不存在权重为负值时,在对dist数组进行更新时,i,j两个顶点的更新顺序的颠倒并不会影响到最终的dist数组的结果,因为dist[i]<=martix[j][i]+dist[j].但当图中存在权重为负值时,dist数组中节点的更新顺序就会影响到最终的结果.为了避免更新顺序造成的"错误",我们可以对节点中的值更新n次(其实n-1次就够了),通过松弛n-1次可以大概率的屏蔽更新顺序的影响.

public boolean bellmanFord(char src,int[] dist,int[] pPath){
		// 初始化和Dijkstra算法一样
        int srcIndex = getIndexOfV(src);
        Arrays.fill(dist,INF);
        dist[srcIndex] = 0;
        Arrays.fill(pPath,-1);
        dist[srcIndex] = 0;
        int n = V.length;

        // 存在负权需要对每个点松弛n-1次.
        for(int k = 0;k < n; k++) {
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    if (matrix[i][j] != INF && dist[i] + matrix[i][j] < dist[j]) {
                        dist[j] = dist[i] + matrix[i][j];
                        pPath[j] = i;
                    }
                }
            }
        }
		// 对dist数组进行验证,看是否存在当前情况下的dist[i]不是最小值的情况
        for(int i = 0; i < n; i++){
            for(int j = 0; j < n; j++){
                if(matrix[i][j] != INF && dist[i]+matrix[i][j] < dist[j]){
                    return false;
                }
            }
        }
        return true;
    }

Floyd-WarShall算法

上述介绍的Dijkstra算法和Bellman-Ford算法解决的都是单源最短路径问题,而Floyd-WarShall算法解决的是多源最短路径问题,既可以实现任意两个点之间的最短路径求解
Floyd-WarShall算法采用的是区间dp的思想.
首先维护一个二维数组dist[][]和二维数组pPath[][],其中dist[i][j]表示从顶点i到顶点j的距离,pPath[i][j]表示的是顶点i到顶点j的最短路径中距离顶点j最近的上一个顶点对应的下标.
考虑这样一个现象,假设顶点i和顶点j的最短路径会经过顶点k,那么dist[i][j] = dist[i][k]+dist[k][j](也就是动态规划中的转移方程).通过这个方程我们实现最短路径的求解.
在求解之前,我们需要先对dist[i][j]数组进行初始化,dist[i][j] = matrix[i][j],pPath[i][j] = i,dist[i][i] = 0.

 public void floydWarShall(int[][] dist,int[][] pPath){
        int n = V.length;
        //pPath[i][j]表示i-j的最短路径上j的前一个点为pPath[i][j]

        //初始化:dist[i][i] = 0,dist[i][j] = martix[i][j]
        for(int i = 0; i < n; i++){
            for(int j = 0; j < n; j++){
                if(matrix[i][j] != INF){
                    dist[i][j] = matrix[i][j];
                    pPath[i][j] = i;
                 }else{
                    dist[i][j] = INF;
                    pPath[i][j] = -1;
                }
                if(i == j){
                    dist[i][j] = 0;
                    pPath[i][j] = -1;
                }
            }
        }

        //更新:以第k个点为中间结点中转的过程
        for(int k = 0; k < n; k++){
            for(int i = 0; i < n; i++){
                for(int j = 0; j < n; j++){
                    if(dist[i][k] != INF && dist[k][j] != INF && dist[i][k] + dist[k][i] < dist[i][j]){
                        dist[i][j] = dist[i][k] + dist[k][j];
                        pPath[i][j] = pPath[k][j];
                    }
                }
            }
        }
    }
}