函数零点计算

前言  

针对任意连续函数的二分法、Aitken方法和牛顿法的实现，以

为例。（默认大家已熟悉算法原理）

一、二分法

（1）定义函数

function F=F(x)
F=x.^3-x-1
end

（2）二分法

a=-9%区间左端点
b=3%区间右端点
format long
if F(a)==0
   fprintf('x=%d is a root',a)
elseif F(b)==0
    fprintf('x=%d is a root',b)
elseif F(a)*F(b)<0
    for i=1:50
        dominl(1)=a
        dominr(2)=b
        domin=[dominl(i),dominr(i)]
        c(i)=sum(domin)/2
        A=F(c(i)).*F(domin)>0
        if A==zeros(1,2)
           fprintf('x=%d is a root',c(i))
        else
           dominl(i+1)=sum((1-A).*domin)
           dominr(i+1)=c(i)
        end
        fprintf('x=%d是一个近似根',c(i))
    end
else
disp('一般二分法不能判断函数在该区间上是否有根(建议对区间分段)')
end
t=a:0.1:b;
plot(F(t))
p=[1 0 -1 -1]
roots(p)

（3）结果

（二）Aitken方法

（1）定义函数

function G=G(x)
G=power(x+1,1/3)%G(x)必须是连续函数
end

（2）判断收敛性

a=1.2%区间左端点
b=1.4%区间右端点
syms x
G1(x)=diff(G(x))
fmin=fminbnd(@(x)G(x),a,b)
fmax=fminbnd(@(x)-G(x),a,b)
dfmax=fminbnd(@(x)-abs(G1(x)),a,b)
dfmin=fminbnd(@(x)abs(G1(x)),a,b)
A=[]
A(1)=a<G(fmin)<b
A(2)=a<G(fmin)<b
A(3)=abs(G1(dfmax))<1
if A==ones(1,3)
    disp('全局收敛')
elseif abs(G1(dfmin))<1
    disp('存在局部收敛，建议缩小区间')
else 
    disp('在该区间不存在收敛子区间，建议寻找其他可能的根区间或更换等价方程')
end

（3）Aitken方法

y0=1.3%任意取收敛区间中的一个数
format long
for i=1:50
    x0(1)=y0
    x1(i)=G(x0(i))
    x2(i)=G(x1(i))
    x(i)=x0(i)-(power(x0(i)-x1(i),2))/(x0(i)-2*x1(i)+x2(i))
    if abs(x(i)-x0(i))>eps
        x0(i+1)=x(i)
    else
        fprintf('%d是近似根',x(1,end-1))
       break
    end
end

% p=[1 0 -3 1]
% roots(p)

（4）结果

（三）牛顿法

（1）一般牛顿法

x0=1.3
syms x
F1(x)=diff(F(x))
for i=1:100

    x1=x0-F(x0)/F1(x0)
    if abs(x0-x1)<eps
        fprintf('%d is a root',x1)
    else
        x0=x1
    end
end

（2）结果

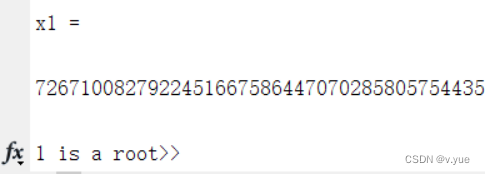
 总结

  牛顿法的算法，我尝试了、和函数，近似解的效果都不错，但是在面对时就不太行，我也不知道为什么。