今天课堂上学习了自己动手构建神经网络,在这里进行一个回顾与总结。
代码需要导入的库以及设置。
from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt
#from sklearn.neural_network import MLPClassifier #多层神经网络
from warnings import simplefilter
simplefilter(action='ignore', category=FutureWarning)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号首先,先定义定义一个层的类和激活函数层类,这里只使用到了Sigmoid和ReLU。
# 定义一个layer
class Layer:
def __init__(self):
pass
#前向计算
def forward(self, input):
return input
#反向传播
def backward(self, input, grad_output):
pass
# 定义Sigmoid激活层
class Sigmoid(Layer):
def __init__(self):
pass
def _sigmoid(self,x):
return 1.0/(1+np.exp(-x))
#前向计算
def forward(self,input):
return self._sigmoid(input)
#反向传播,算梯度
def backward(self,input,grad_output):
sigmoid_grad = self._sigmoid(input)*(1-self._sigmoid(input)) # 对Sigmoid函数进行求导
return grad_output*sigmoid_grad
#定义ReLU激活层
class ReLU(Layer):
def __init__(self):
pass
def forward(self,input):
return np.maximum(0,input) # relu函数为max(0,x)
def backward(self,input,grad_output):
relu_grad = input>0 #relu函数导数为1 if x>0 else 0
return grad_output*relu_grad之后再定义一个隐藏层。
隐藏层初始化时需要输入传入的数据大小,传出数据的大小,以及学习率。之后会自动生成初始的weights和biases。
#隐藏层
class Dense(Layer):
def __init__(self, input_units, output_units, learning_rate=0.8):
self.learning_rate = learning_rate
self.weights = np.random.randn(input_units, output_units)#初始化影响很大
self.biases = np.zeros(output_units)
def forward(self,input):
return np.dot(input,self.weights)+self.biases
def backward(self,input,grad_output):
# 计算梯度
grad_input = np.dot(grad_output, self.weights.T)
grad_weights = np.dot(input.T,grad_output)/input.shape[0]
grad_biases = grad_output.mean(axis=0)
# 梯度下降
self.weights = self.weights - self.learning_rate*grad_weights
self.biases = self.biases - self.learning_rate*grad_biases
return grad_input接下来,实现一个基本的多层神经网络。
#基本的多层神经网络
class MLPClassifier(Layer):
def __init__(self):
self.network = [] # 设置一个存放层的列表,将使用的每一层添加到该列表中
self.network.append(Dense(2,64))
self.network.append(ReLU())
self.network.append(Dense(64,32))
self.network.append(Sigmoid())
self.network.append(Dense(32,16))
self.network.append(Sigmoid())
self.network.append(Dense(16,1))
self.network.append(Sigmoid())
def forward(self,X):
self.activations = [] # 用于存储每一层的输出结果
input = X
for layer in self.network:
self.activations.append(layer.forward(input))
input = self.activations[-1] # 每一层的输出作为下一层的输入,所以input等于self.activations[-1]
assert len(self.activations) == len(self.network)
return self.activations
def predict(self,X):
y_pred = self.forward(X)[-1] # 将最后一个输出的值作为最终的值,进行分类
y_pred[y_pred>0.5] = 1 # 因为上面最后一个输出经过了Sigmoid函数,所以所有的值会被调整为0-1之间
y_pred[y_pred<=0.5] = 0
return y_pred
def predict_proba(self,X):
logits = self.forward(X)[-1]
return logits
def train(self,X,y):
# 先前向计算,再反向传播,梯度下降更新权重参数w,b
self.forward(X)
layer_inputs = [X]+self.activations # 因为actiations只包含每一层的输出,而不包含最开始的输入X,所以将X添加到layer_inputs中
logits = self.activations[-1]
# 损失函数需要自己定义,这里使用均方误差函数(MSE)
loss = np.square(logits - y.reshape(-1,1)).sum()
loss_grad = 2.0*(logits-y.reshape(-1,1))
for layer_i in range(len(self.network))[::-1]: # 因为是进行反向传播,所以是从后往前进行传播,所以需要将range(len(self.network))进行反转。
layer = self.network[layer_i] # 根据layer_i判断当前是第几层
loss_grad = layer.backward(layer_inputs[layer_i],loss_grad) # 调用该层的反向传播方法。
return np.mean(loss)最后通过一个数据集来进行分类,同时绘制损失值的图像。
# 使用半月形数据集
x_train,y_train = datasets.make_moons(n_samples=1000,noise=0.2,random_state=666)
plt.scatter(x_train[y_train==0,0],x_train[y_train==0,1])
plt.scatter(x_train[y_train==1,0],x_train[y_train==1,1])
# 神经网络实例化,同时绘制损失的图像。
MLP = MLPClassifier()
losses=[]
for e in range(3000):
loss = MLP.train(x_train,y_train)
losses.append(loss)
plt.plot(losses)
plt.grid()最后,绘制边界观察分类效果如何。
#画边界线
def plot_decision_boundary(model, X, y):
x0_min, x0_max = X[:,0].min()-1, X[:,0].max()+1
x1_min, x1_max = X[:,1].min()-1, X[:,1].max()+1
x0, x1 = np.meshgrid(np.linspace(x0_min, x0_max, 100), np.linspace(x1_min, x1_max, 100))
Z = model.predict(np.c_[x0.ravel(), x1.ravel()])
Z = Z.reshape(x0.shape)
plt.contourf(x0, x1, Z, cmap=plt.cm.Spectral)
plt.ylabel('x1')
plt.xlabel('x0')
plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(y))
plot_decision_boundary(MLP,x_train,y_train)具体的分类效果可以通过在上面的定义神经网络中修改层数,输出大小,学习率以及最后通过的激活函数来对比不同的效果。
这是自己得出的结果。
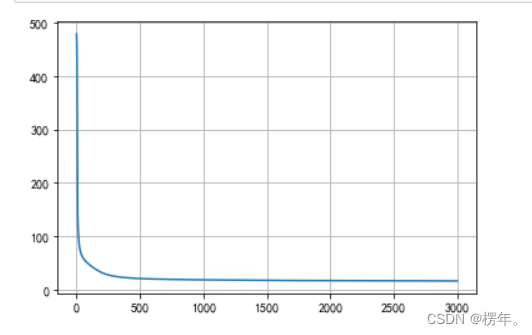

以上是自己对学习完神经网络的一些观点,如有意见欢迎指正。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








