L1-SVD算法原理

1.联合时间的逆问题

首先给出多快拍下的远场窄带接收信号模型，如下式所示：

这里有个前提（先验）：假设信号S必须在空域上稀疏，在时域上不必稀疏。

计算S中每一空域方向上所有快拍的范数：

并加入S的范数惩罚函数（增强稀疏度）：

2.SVD处理

为了降低计算复杂度和对噪声的敏感度，采用奇异值分解(singular value decomposition,SVD)的方法，将Y分解为信号子空间和噪声子空间，从T维降到K维，（T是快拍数，K是信源个数），只保留信号子空间，不保留噪声子空间（MUSIC,Pisarenko和最小范数子空间方法需要保留噪声子空间），从而估计出A中的哪些列组合成信号子空间。SVD如下式：

其中 表示KxK阶单位矩阵，表示Kx(T-K)阶

-SVD具体流程框图如下

通过降维后，原问题就变成了

3.二阶锥规划(second-order cone programming,SOCP)问题

上述问题中包含以下式子：

该式既不是线性的，也不是二次的，所以我们将其转化为一个二阶锥规划，二阶锥规划通常可以处理以下锥约束形式：

二阶锥规划对于包含二阶锥，凸二次型以及线性形式的目标函数最优化来说，是一个比较合适的方法，考虑选择SOC规划，而不是一般非线性最优化解决该问题的主要原因是内点算法对求数值解的有效性。除了能获得有效数值解外，SOC规划具有坚实的理论基础，是半定规划与凸圆锥规划的一种特殊情形。

我们将上述问题转化为二次锥规划形式：

这里提醒一个常用的处理方法：目标函数里的p和q分别是原目标函数对应式子的上界，就是只要使p，q最小，原式的值就能取到最小，因为p，q的最小值最多只能取到原式的最小值（下界），不可能比原式的最小值还要小。

4.将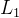-SVD转化为SOCP详细证明

首先引入辅助变量p和q，目的是将非线性放到约束里面去，使目标函数变为线性的：

由于第二个约束条件中等号左边式子是非负实值（因为有范数），所以可转化为以下式子：

其中代表全为1的N维列向量。

观察式子

可以进一步转化为

最终得到

从上式可以看出，目标函数是线性的，约束条件集合包括二次，线性以及二阶锥形式。