7-32 哥尼斯堡的“七桥问题”,自己做两个测试点递归解决超时(焯:
#include <bits/stdc++.h>
using namespace std;
vector<int> path;
vector<vector<bool>> graph;
vector<vector<bool>> edge;
int n,m,v1,v2;
bool flag=false;
void dfs(int start,int v,int cnt){
if (flag) return;
//v是当前访问点,start是起点,edge是已经走过的边,cnt是走过边的数目
if (cnt==m){
if (start==v) flag=true;
return;
}
//从这个点出发,尝试走那些没走过的边
for (int w=0;w<n;w++){ //v->w有路并且没有走过
if (graph[v][w] && !edge[v][w]){
edge[v][w]=1;edge[w][v]=1;
cnt++;
dfs(start,w,cnt);
edge[v][w]=0;edge[w][v]=0;
cnt--;
}
}
}
int main(){
//包含所有边且从起点回到自己的路径不重复
scanf("%d %d",&n,&m);
//dfs走遍所有所有长度为m的路径
//记录走过边的情况和当前到达点的情况,判断是否存在
graph.resize(n);
for (int i=0;i<n;i++) graph[i].push_back(false);
edge.resize(n);
for (int i=0;i<n;i++) edge[i].push_back(false);
for (int i=0;i<m;i++){
scanf("%d %d",&v1,&v2);
graph[v1-1][v2-1]=true;
graph[v2-1][v1-1]=true;
}
//记录走过的边,每走过一条边就把两个点对应的边设为1
for (int start=0;start<n;start++){
dfs(start,start,0);
if (flag){
printf("1");
return 0;
}
flag=false;
edge.clear();
}
printf("0");
}
用定理判断:图连通 + 所有节点度数都是偶数
- 如果需要记录 DFS 和 BFS 的步数,即从起始点到当前节点走过的步数:
- DFS 可以加全局变量 step,回溯法处理
- BFS 可以记录每层的最后一个节点,当访问每层的最后一个节点之后 step++
- 图论相关内容:
- 简单图: 每条边连接着两个不同的顶点(没有自回路);没有两条边连接着同一对顶点(没有重边)
- 多重图:简单图的两条性质都可以打破
- 简单路径:路径上的顶点都不相同
- 同构图:两个图的顶点集存在一个一一映射 f,并且一个图中邻接的两个顶点在映射后仍然邻接
- 图不变量:只和抽象图结构相关的属性,同构图的任何图不变量都相等,即若两个图的某个图不变量不相等,这两个图必然不同构。图不变量包括顶点数量,边数量,顶点度集合
- 关节点/割点:移除该点和该点连接的边后,图的连通分量变多的那些点,边也有类似的概念,术语是 桥
- 点割集/分离集:移除分离集中的点之后图不再连通,边也有类似概念,术语是 边割集
- 点连通度:点割集的最少点数。如果图的点连通度是 k,图是 j-点连通的(j<=k),边也有类似概念,连通度是图不变量
- 欧拉回路/欧拉路径:包含所有边的简单回路/简单路径,点也有类似概念,术语是 哈密尔顿回路/哈密尔顿路径
- 对于多重图:每个顶点度都是偶数 ⟺ \iff ⟺至少有两个不同的点间有欧拉回路;有且仅有两个顶点度是奇数 ⟺ \iff ⟺图有欧拉路径
- 对于顶点数n >=3 的简单图:每个顶点的度>=n/2 ⇒ \Rightarrow ⇒ 有哈密尔顿回路;任意不邻接的顶点 u 和 v,deg(u)+deg(v)>=n ⇒ \Rightarrow ⇒ 有哈密尔顿回路
- 一些图:
-
完全图 K n K_n Kn:简单图且每个顶点都和其他n-1个顶点相连

-
环 C n C_n Cn:顶点数n>=3,包含边 { v 1 , v 2 } , { v 2 , v 3 } , . . . , { v n − 1 , v n } \{v_1,v_2\},\{v_2,v_3\},...,\{v_{n-1},v_n\} {v1,v2},{v2,v3},...,{vn−1,vn}
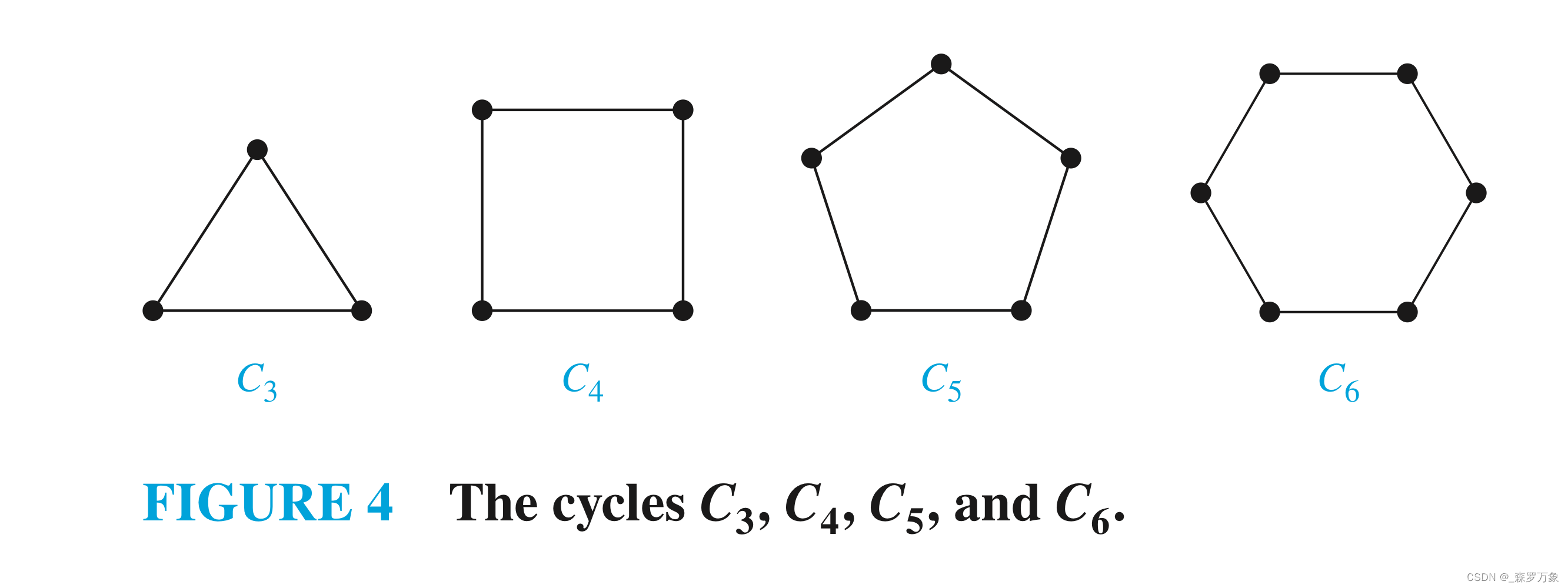
-
轮 W n W_n Wn:在轮 C n C_n Cn中心添加一个点,并与环上的点都相连
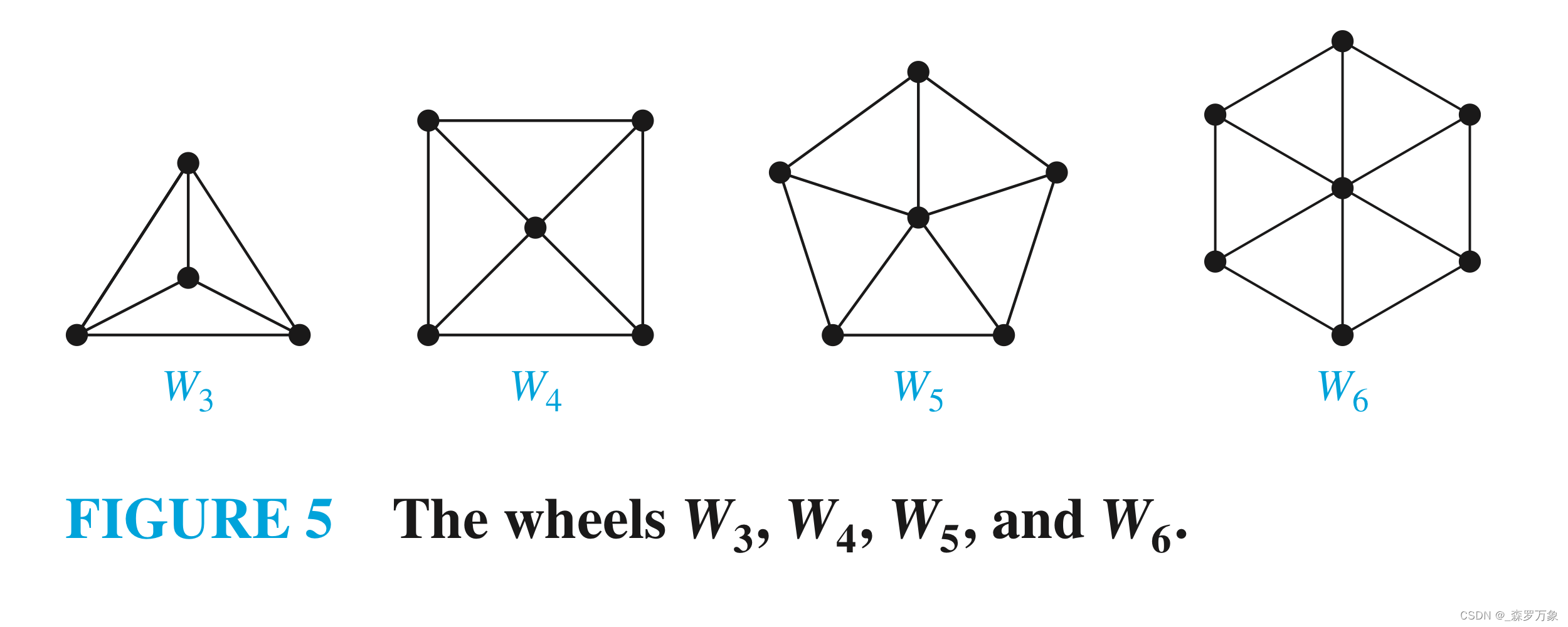
-
超立方体 Q n Q_n Qn: 2 n 2^n 2n个点的超立方体图,每个点由长度为n的字符串表示,当两个点的字符串表示恰好只有1位不同时它们之间有边相连

-
- 平面图:在一个平面上,没有任何边(可以是直线或曲线)相交的图
- 欧拉定理:一个平面简单图有 e 条边和 v 个顶点,r 是平面图分成的区域, r = e − v + 2 r = e - v + 2 r=e−v+2
- 一个平面简单图有 e 条边和 v 个顶点,v>=3 ⇒ \Rightarrow ⇒ e<=3v-6,若没有长度为3的回路,则进一步 e<=2v-4
- 一个平面简单图,任意顶点的度不超过5
- 初等分割:移去图的边 { u , v } \{u,v\} {u,v},再添加顶点 w w w 和 边 { w , v } , { u , w } \{w,v\},\{u,w\} {w,v},{u,w} 得到一个新图。一个平面图通过初等分割仍然是平面图
- 同胚图:从同一个图出发经过一系列初等分割得到的图
- 图不是平面图 ⟺ \iff ⟺ 包含 K 3 , 3 K_{3,3} K3,3 和 K 5 K_{5} K5 的同胚子图
- 对偶图:一个图的每个区域对应一个点,若区域有公共边(只在一点相接的情况除去),则对应的的点相连
- 简单图的着色:每个点分配一种颜色,相连的点颜色不同
- 色数:完成简单图着色所需最少颜色数,用 χ ( G ) \chi(G) χ(G) 表示
- 四色定理:平面图的色数不超过4
- 从图的顶点 i 到 j 有长度为 r 的
A
i
j
r
A^{r}_{ij}
Aijr 不同路径数,累乘邻接矩阵可以:
- 求得任意顶点间的不同路径条数
- 检验图是否连通
- 求得两点直接的最短路径长度
void DFS(int v){
//O(N^2)
//从起始点访问到v这个节点已经走了step步
cout << v << ' ';
visited[v]=true;
for (int i=0;i<nV;i++){
if (weightedG[v][i]!=(weightType)0 && !visited[i]){
step++;
DFS(i);
step--;
}
}
}
//☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆
//☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆
void BFS(int v){
//O(N^2)
queue<int> q;
visited[v]=true;
q.push(v);
int last=v; //第一层只有一个元素,自己就是队尾
cout << v << ' ';
while (!q.empty()){
int w=q.front();q.pop(); //从起始点访问到w这个节点已经走了step步
for (int i=0;i<nV;i++){
if (weightedG[w][i]!=(weightType)0 && !visited[i]){
cout << i << ' ';
visited[i]=true;
q.push(i);
}
}
}
if (w==last){
last=q.back(); //这一层已经全部访问,下一层已经全部入队,下一层的最后一个节点就是队尾的
step++;
}
}
#include <iostream>
#include <queue>
#define MaxSize 100
using namespace std;
template<typename weightType>
class mEdge{
public:
int v1,v2;
weightType weight;
mEdge(int _v1,int _v2,weightType _weight):v1(_v1),v2(_v2),weight(_weight){};
};
template<typename weightType,typename dataType>
class mGraph{
public:
//邻接矩阵表示的有权图
//图是一种多对多关系,是链表和树的扩展
//(v,w)是无向边,<v,w>是有向边
//图的数据包括非空有限顶点集和有限边集
//{G_00,G_10,G_11,...,G_n-1n-1}可以省一半空间,Gij的下标是(i*(i+1)/2+j)
//☆有权图如果没有边应该怎么表示?☆
int nV,nE; //边数和顶点数
weightType weightedG[MaxSize][MaxSize]={0}; //带权重的图
dataType data[MaxSize]={0}; //存每个顶点的数据
bool visited[MaxSize]={false}; //遍历图需要
mGraph(int vertexNum):nE(0),nV(vertexNum){};
void InsertEdge(mEdge<weightType>* e){
if (e->v1>=nV && e->v2>=nV){
cout << "边的顶点违法" << endl;
return;
}
weightedG[e->v1][e->v2]=e->weight;
nE++;
}
void DFS(int v){
//O(N^2)
cout << v << ' ';
visited[v]=true;
for (int i=0;i<nV;i++){
if (weightedG[v][i]!=(weightType)0 && !visited[i]) DFS(i);
}
}
void reSetVisited(){
//遍历结束之后需要重置visited方便下次遍历
for (int i=0;i<nV;i++) visited[i]=false;
}
//☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆
//☆☆☆☆这里必须这么写,不能在while里cout w,会有重复☆☆☆☆
//☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆
void BFS(int v){
//O(N^2)
queue<int> q;
visited[v]=true;
q.push(v);
cout << v << ' ';
while (!q.empty()){
int w=q.front();q.pop();
for (int i=0;i<nV;i++){
if (weightedG[w][i]!=(weightType)0 && !visited[i]){
cout << i << ' ';
visited[i]=true;
q.push(i);
}
}
}
}
};
template<typename weightType>
class EdgeAndNode{ //□-
public:
weightType weight;
int vertexIndex;
EdgeAndNode<weightType>* next;
EdgeAndNode(weightType w,int i):weight(w),vertexIndex(i),next(nullptr){};
EdgeAndNode(weightType w,int i,EdgeAndNode<weightType>* n):weight(w),vertexIndex(i),next(n){};
};
template<typename weightType>
class lEdge{
public:
int v1,v2;
weightType weight;
lEdge(int _v1,int _v2,weightType w):v1(_v1),v2(_v2),weight(w){};
};
template<typename weightType,typename dataType>
class firstNode{ //□
public:
dataType data;
int vertexIndex;
EdgeAndNode<weightType>* firstEdge;
firstNode(dataType d,int i):data(d),vertexIndex(i),firstEdge(nullptr){};
};
template<typename weightType,typename dataType>
class lGraph{
public:
int nV,nE; //边数和顶点数
firstNode<weightType,dataType>* weightedG[MaxSize]; //带权重的图
bool visited[MaxSize]={false}; //遍历图需要
lGraph(int vertexNum){
nV=vertexNum;nE=0;
for (int i=0;i<nV;i++) weightedG[i]=new firstNode<weightType,dataType>((dataType)-1,i);
}
lGraph(int vertexNum,dataType data[]){
nV=vertexNum;nE=0;
for (int i=0;i<nV;i++) weightedG[i]=new firstNode<weightType,dataType>(data[i],i);
}
void InsertEdge(lEdge<weightType>* e){
int i;
for (i=0;i<nV && weightedG[i]->vertexIndex!=e->v1;i++);
if (i==nV){
cout << "边的起点不存在" << endl;
return;
}
EdgeAndNode<weightType>* tmp=new EdgeAndNode<weightType>(e->weight,e->v2,weightedG[i]->firstEdge);
weightedG[i]->firstEdge=tmp;
}
void DFS(int v){
visited[v]=true;
cout << v << ' ';
EdgeAndNode<weightType>* tmp=weightedG[v]->firstEdge;
while (tmp){
if (!visited[tmp->vertexIndex]) DFS(tmp->vertexIndex);
tmp=tmp->next;
}
}
void BFS(int v){
//遍历当前节点的邻接节点并入队
queue<int> q;
q.push(v);
cout << v << ' ';
visited[v]=true;
while (!q.empty()){
int w=q.front();q.pop();
EdgeAndNode<weightType>* tmp=weightedG[w]->firstEdge;
while (tmp){
if (!visited[tmp->vertexIndex]){
cout << tmp->vertexIndex << ' ';
visited[tmp->vertexIndex]=true;
q.push(tmp->vertexIndex);
}
tmp=tmp->next;
}
}
}
};
int main(){
int vertexNum,edgeNum;
cin >> vertexNum;
mGraph<int,int>* mg=new mGraph<int,int>(vertexNum);
//lGraph<int,int>* lg=new lGraph<int,int>(vertexNum);
cin >> edgeNum;
for (int i=0;i<edgeNum;i++){
int v1,v2,weight;
cin >> v1 >> v2 >> weight;
mEdge<int>* e=new mEdge<int>(v1,v2,weight);
//lEdge<int>* e=new lEdge<int>(v1,v2,weight);
mg->InsertEdge(e);
//lg->InsertEdge(e);
}
mg->BFS(0);
//lg->BFS(0);
return 0;
}


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










