目录
相关定义(队列将在BFS用到)
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#define TRUE 1
#define FALSE 0
#define MAXSIZE 100
#define MaxVertexNum 100 //最大顶点数
#define Infinity 65535 //表示 ∞
#define OK 1
#define ERROR 0
typedef int VertexType; //顶点数据类型,数字为例
typedef int EdgeType;
typedef int Status;
typedef struct{ //无向图的邻接矩阵
VertexType data[MaxVertexNum]; //顶点数据数组
EdgeType edge[MaxVertexNum][MaxVertexNum]; //邻接矩阵数组
int vertexnum, edgenum; //顶点数,边数
}MGraph;
typedef int QElemType;
typedef struct{
QElemType data[MAXSIZE];
int front, rear;
}SqQueue;
//初始化队列
Status InitQueue(SqQueue *Q){
Q->front=Q->rear=0;
return OK;
}
//判断队列空否
Status QueueEmpty(SqQueue *Q){
if(Q->front == Q->rear)
return TRUE;
else return FALSE;
}
//判断队列满否
Status QueueFull(SqQueue *Q){
if((Q->rear+1)%MAXSIZE == Q->front)
return TRUE;
else return FALSE;
}
//入队
Status EnQueue(SqQueue *Q, QElemType e){
if((Q->rear+1)%MAXSIZE == Q->front){
printf("队列满,无法入队!");
return ERROR;
}
Q->data[Q->rear]=e;
Q->rear=(Q->rear+1)%MAXSIZE;
return OK;
}
//出队
Status DeQueue(SqQueue *Q, QElemType *e){
if(Q->front == Q->rear){
printf("队列空,无法出队!");
return ERROR;
}
*e = Q->data[Q->front];
Q->front=(Q->front+1)%MAXSIZE;
return OK;
}创建无向网(邻接矩阵存储)
void CreateMGraph(MGraph *G){ //无向网
int i, j, k=0;
VertexType v1, v2;
EdgeType w;
printf("输入顶点数及边数(逗号隔开):");
scanf("%d,%d", &G->vertexnum, &G->edgenum); //具体顶点数,边数
for(i=0;i<G->vertexnum;i++){
G->data[i]=i;
}
for(i=0;i<G->vertexnum;i++)
for(j=0;j<G->vertexnum;j++)
G->edge[i][j]=Infinity; //初始化邻接矩阵(边全为∞)
printf("为顶点之间创造边(Vi,Vj)以及权重(空格隔开):\n");
for(;k<G->edgenum;k++){
scanf("%d,%d %d", &v1, &v2, &w);
if(v1==-1||v2==-1)
{
printf("图中无此顶点!\n");
return;
}
G->edge[v1-1][v2-1]=w;
G->edge[v2-1][v1-1]=w; //对称矩阵
}
}打印邻接矩阵
void Display(MGraph G)
{
int i,j;
printf("\n-------------------------------");
printf("\n 邻接矩阵:\n\n");
printf("\t ");
for(i=0;i<G.vertexnum;i++)
printf("\t%d",G.data[i]+1);
printf("\n");
for(i=0;i<G.vertexnum;i++)
{
printf("\t%d",G.data[i]+1);
for(j=0;j<G.vertexnum;j++)
{
if(G.edge[i][j]==Infinity)
printf("\t∞");
else printf("\t%d",G.edge[i][j]);
}
printf("\n");
}
}Prim算法得最小生成树
void MiniSpanTree_Prim(MGraph G){
int min, i, j, k;
int adjvex[MaxVertexNum];
int lowcost[MaxVertexNum];
lowcost[0]=0;
adjvex[0]=0;
for(i=0;i<G.vertexnum;i++){
lowcost[i]=G.edge[0][i];
adjvex[i]=0;
}
for(i=1;i<G.vertexnum;i++){
min=Infinity;
j=1; k=0;
while(j<G.vertexnum){
if(lowcost[j]!=0 && lowcost[j]<min){
min=lowcost[j];
k=j;
}
j++;
}
printf("(%d,%d), %d\n", adjvex[k]+1, k+1, G.edge[adjvex[k]][k]);
lowcost[k]=0;
for(j=1;j<G.vertexnum;j++){
if(lowcost[j]!=0 && G.edge[k][j]<lowcost[j]){
lowcost[j]=G.edge[k][j];
adjvex[j]=k;
}
}
}
}BFS
//递归BFS
void BFS(MGraph G){
int i, j;
SqQueue Q; InitQueue(&Q);
for(i=0;i<G.vertexnum;i++)
visited[i]=FALSE;
for(i=0;i<G.vertexnum;i++){ //每个顶点走一遍
if(!visited[i]){
printf("%d", G.data[i]+1); //访问Vi
visited[i]=TRUE; //标记已访问
EnQueue(&Q,i); //将其下标入队
while(!QueueEmpty){
DeQueue(&Q,&i); //队头元素出队给i
for(j=0;j<G.vertexnum;j++){
// 判断其它顶点若与当前顶点存在边且未访问过
if((G.edge[i][j]==1) && !visited[j]){
printf("%d", G.data[j]+1);
visited[j]=TRUE;
EnQueue(&Q,j); //Vj访问后就入队
}
}
}
}
}
}DFS
enum{False,True} visited[MaxVertexNum]; //访问标志
//递归DFS
void DFSM(MGraph G, int i){ //从Vi开始的DFS
int j;
printf("%d", G.data[i]+1); //访问
visited[i]=TRUE; //标记已访问
for(j=0;j<G.vertexnum;j++){
if((G.edge[i][j]!=Infinity) && !visited[j]){
DFSM(G, j); //(Vi,Vj)存在且Vj没被访问,则又从Vj出发寻找下一个邻接点
}
}
}
void DFS(MGraph G){ //整个图的DFS遍历
int i;
for(i=0;i<G.vertexnum;i++){
visited[i]=FALSE;
}
for(i=0;i<G.vertexnum;i++){
if(!visited[i])
DFSM(G,i);
}
}整体代码:
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#define TRUE 1
#define FALSE 0
#define MAXSIZE 100
#define MaxVertexNum 100 //最大顶点数
#define Infinity 65535 //表示 ∞
#define OK 1
#define ERROR 0
typedef int VertexType; //顶点数据类型,数字为例
typedef int EdgeType;
typedef int Status;
typedef struct{ //无向图的邻接矩阵
VertexType data[MaxVertexNum]; //顶点数据数组
EdgeType edge[MaxVertexNum][MaxVertexNum]; //邻接矩阵数组
int vertexnum, edgenum; //顶点数,边数
}MGraph;
typedef int QElemType;
typedef struct{
QElemType data[MAXSIZE];
int front, rear;
}SqQueue;
//初始化队列
Status InitQueue(SqQueue *Q){
Q->front=Q->rear=0;
return OK;
}
//判断队列空否
Status QueueEmpty(SqQueue *Q){
if(Q->front == Q->rear)
return TRUE;
else return FALSE;
}
//判断队列满否
Status QueueFull(SqQueue *Q){
if((Q->rear+1)%MAXSIZE == Q->front)
return TRUE;
else return FALSE;
}
//入队
Status EnQueue(SqQueue *Q, QElemType e){
if((Q->rear+1)%MAXSIZE == Q->front){
printf("队列满,无法入队!");
return ERROR;
}
Q->data[Q->rear]=e;
Q->rear=(Q->rear+1)%MAXSIZE;
return OK;
}
//出队
Status DeQueue(SqQueue *Q, QElemType *e){
if(Q->front == Q->rear){
printf("队列空,无法出队!");
return ERROR;
}
*e = Q->data[Q->front];
Q->front=(Q->front+1)%MAXSIZE;
return OK;
}
void Display(MGraph G)
{
int i,j;
printf("\n-------------------------------");
printf("\n 邻接矩阵:\n\n");
printf("\t ");
for(i=0;i<G.vertexnum;i++)
printf("\t%d",G.data[i]+1);
printf("\n");
for(i=0;i<G.vertexnum;i++)
{
printf("\t%d",G.data[i]+1);
for(j=0;j<G.vertexnum;j++)
{
if(G.edge[i][j]==Infinity)
printf("\t∞");
else printf("\t%d",G.edge[i][j]);
}
printf("\n");
}
}
void CreateMGraph(MGraph *G){ //无向网
int i, j, k=0;
VertexType v1, v2;
EdgeType w;
printf("输入顶点数及边数(逗号隔开):");
scanf("%d,%d", &G->vertexnum, &G->edgenum); //具体顶点数,边数
for(i=0;i<G->vertexnum;i++){
G->data[i]=i;
}
for(i=0;i<G->vertexnum;i++)
for(j=0;j<G->vertexnum;j++)
G->edge[i][j]=Infinity; //初始化邻接矩阵(边全为∞)
printf("为顶点之间创造边(Vi,Vj)以及权重(空格隔开):\n");
for(;k<G->edgenum;k++){
scanf("%d,%d %d", &v1, &v2, &w);
if(v1==-1||v2==-1)
{
printf("图中无此顶点!\n");
return;
}
G->edge[v1-1][v2-1]=w;
G->edge[v2-1][v1-1]=w; //对称矩阵
}
}
void MiniSpanTree_Prim(MGraph G){
int min, i, j, k;
int adjvex[MaxVertexNum];
int lowcost[MaxVertexNum];
lowcost[0]=0;
adjvex[0]=0;
for(i=0;i<G.vertexnum;i++){
lowcost[i]=G.edge[0][i];
adjvex[i]=0;
}
for(i=1;i<G.vertexnum;i++){
min=Infinity;
j=1; k=0;
while(j<G.vertexnum){
if(lowcost[j]!=0 && lowcost[j]<min){
min=lowcost[j];
k=j;
}
j++;
}
printf("(%d,%d), %d\n", adjvex[k]+1, k+1, G.edge[adjvex[k]][k]);
lowcost[k]=0;
for(j=1;j<G.vertexnum;j++){
if(lowcost[j]!=0 && G.edge[k][j]<lowcost[j]){
lowcost[j]=G.edge[k][j];
adjvex[j]=k;
}
}
}
}
enum{False,True} visited[MaxVertexNum]; //访问标志
//递归DFS
void DFSM(MGraph G, int i){ //从Vi开始的DFS
int j;
printf("%d", G.data[i]+1); //访问
visited[i]=TRUE; //标记已访问
for(j=0;j<G.vertexnum;j++){
if((G.edge[i][j]!=Infinity) && !visited[j]){
DFSM(G, j); //(Vi,Vj)存在且Vj没被访问,则又从Vj出发寻找下一个邻接点
}
}
}
void DFS(MGraph G){ //整个图的DFS遍历
int i;
for(i=0;i<G.vertexnum;i++){
visited[i]=FALSE;
}
for(i=0;i<G.vertexnum;i++){
if(!visited[i])
DFSM(G,i);
}
}
//递归BFS
void BFS(MGraph G){
int i, j;
SqQueue Q; InitQueue(&Q);
for(i=0;i<G.vertexnum;i++)
visited[i]=FALSE;
for(i=0;i<G.vertexnum;i++){ //每个顶点走一遍
if(!visited[i]){
printf("%d", G.data[i]+1); //访问Vi
visited[i]=TRUE; //标记已访问
EnQueue(&Q,i); //将其下标入队
while(!QueueEmpty){
DeQueue(&Q,&i); //队头元素出队给i
for(j=0;j<G.vertexnum;j++){
// 判断其它顶点若与当前顶点存在边且未访问过
if((G.edge[i][j]==1) && !visited[j]){
printf("%d", G.data[j]+1);
visited[j]=TRUE;
EnQueue(&Q,j); //Vj访问后就入队
}
}
}
}
}
}
void main(){
MGraph G;
CreateMGraph(&G);
Display(G);
MiniSpanTree_Prim(G);
printf("Result of DFS traverse:\n");
DFS(G);
putchar('\n');
printf("Result of BFS traverse:\n");
BFS(G);
}示例
通过例子来说明算法操作的结果。
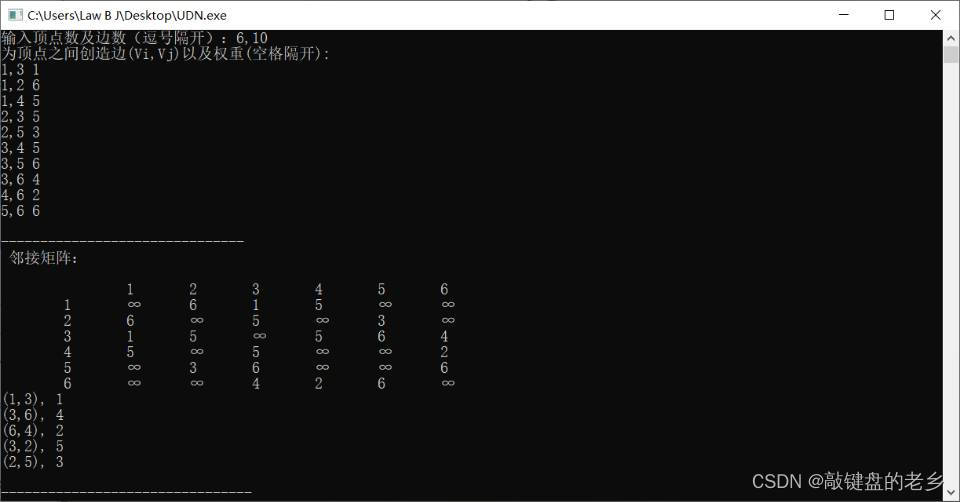
设有下图中给出的无向网

程序运行得到:
最小生成树
BFS和DFS
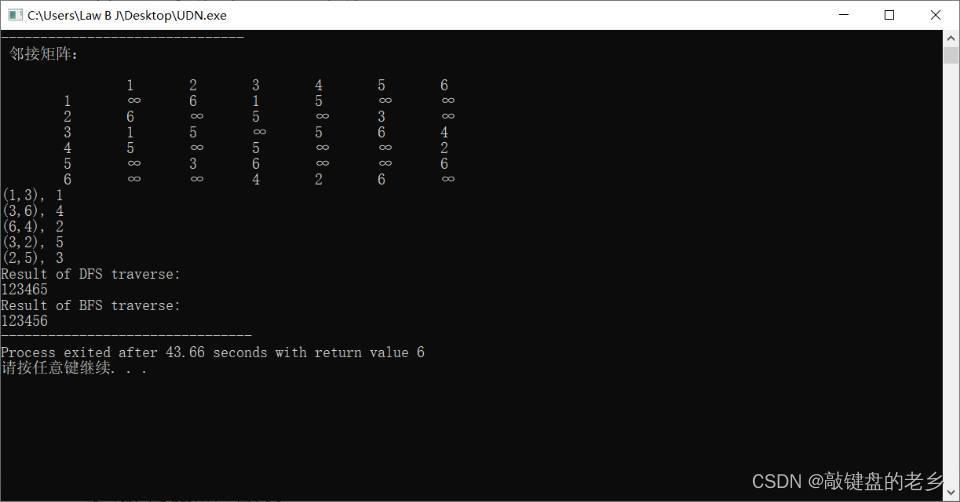








 本文介绍了如何使用邻接矩阵创建无向网,并展示了Prim算法求最小生成树的过程。此外,还详细讲解了广度优先搜索(BFS)和深度优先搜索(DFS)在图中的应用。通过实例演示,读者可以了解算法在实际问题中的运用。
本文介绍了如何使用邻接矩阵创建无向网,并展示了Prim算法求最小生成树的过程。此外,还详细讲解了广度优先搜索(BFS)和深度优先搜索(DFS)在图中的应用。通过实例演示,读者可以了解算法在实际问题中的运用。
















 6217
6217

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








