E - Sugoroku 4(abc)

E - Sugoroku 4

传送门

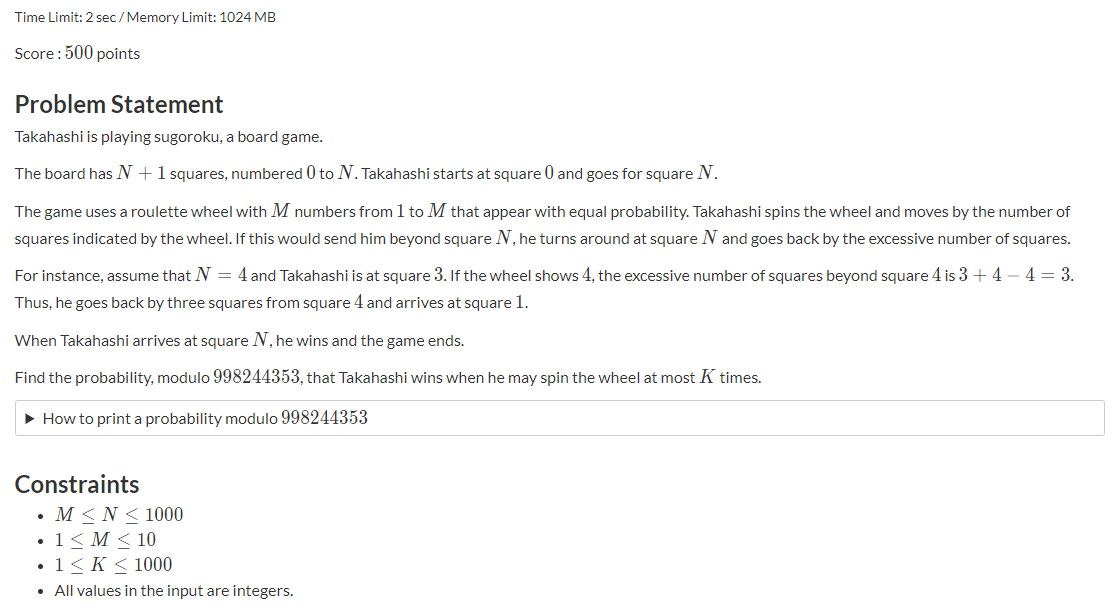
题意：0 - n 长度得数轴，每次走骰子为1-m得长度，若超过长度n则折回超过得长度，总共走k次，统计k次走到n得概率
例如： n = 4, m = 4, k = 3,初始位置为0；
若第一次骰子为3, 0->3；
若第二次骰子为3，3->2;
若第三次骰子为3，2->3.

样例输入

10 5 6

样例输出

184124175

题解：
骰子得概率都为 $\frac{1}{m}$ ,即统计到n得方案数$f$，概率即为$f\ast \frac{1}{m}$;
$\frac{1}{m}$即用乘法逆元表示，即$m^{p-2}$，总共骰k次
$$概率即为\sum _{i=1}^{k}f\ast m^{p-2}$$
$f[i,j]$表示前i次骰子，走到j得方案数.
时间复杂度为$O(nmk+logmod)$

#include <unordered_map>
#include <cstring>
#include <algorithm>
#include <iostream>

using namespace std;
typedef long long LL;
const int N = 1e3 + 10, mod = 998244353;
LL n, m, k;
LL f[N][N];

LL qmi(int a, int b, int p)
{
    LL res = 1;
    while (b)
    {
        if (b & 1) res = res * a % p;
        a = a * (LL)a % p;
        b >>= 1;
    }
    return res;
}

void solve() {
	cin >> n >> m >> k;
	f[0][0] = 1;
	LL p = qmi(m, mod - 2, mod);   
	for(int i = 1; i <= k; i ++ )
	{
		for(int j = 0; j < n; j ++ )
		{
			for(int z = 1; z <= m; z ++ )
			{
				int t = (j + z);
				if(t > n) t = 2 * n - t;
				f[i][t] += (f[i - 1][j] * p) % mod;
				f[i][t] %= mod;
			}
		}
	}
	LL sum = 0;
	for(int i = 1; i <= k; i ++ )
		sum = (sum + f[i][n]) % mod;
	cout << sum << endl;
}

int main() {
	int T = 1;
	while (T--) {
		solve();
	}
	return 0;
}