无约束优化方法----Powell法

Powell法的python实现

前面我们介绍了一维搜索的两种优化方法：黄金分割法以及二次插值法。本节我们介绍无约束优化问题常用的Powell法(本质上是共轭方向法)。

1. Powell法

Powell法将整个计算过程分为若干个阶段，每一个阶段由n+1次一维搜索组成。根据共轭方向的概念以及性质，Powell法的核心思想是：首先沿着坐标轴的方向依次进行一维搜索，然后将初次迭代的起始点与末次迭代得到的一个极值点连接构成一个新方向，并沿新方向进行一次一维搜索，此时完成一轮迭代，然后重复上述迭代过程直至满足终止条件。

1.1 Powell法的迭代步骤

1.2 例题

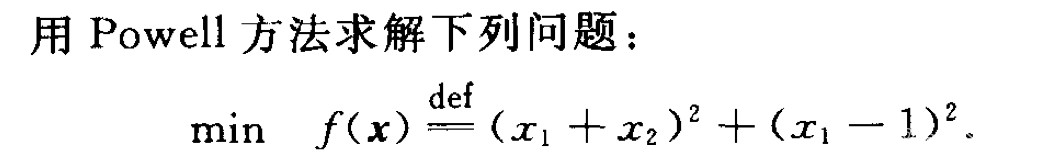
初始点$x^{(0)}=[2,1{]}^T$

1.3 代码

# import package
import sympy as sp
from sympy import *
import numpy as np
import matplotlib.pyplot as plt
import math

# Powell方法
def Powell(f,x1,x2,epsilon,k,S,x_initial,x_point):

    # 沿坐标轴1的方向进行一维搜索
    alpha = symbols('alpha')
    f1 = f.subs({x1:(x_initial+alpha*S[0])[0],x2:(x_initial+alpha*S[0])[1]}).evalf()
    
    # 次数不高,可直接采用求导的方法求极值点
    alpha1 = solve(diff(f1,alpha),alpha)[0]
    x_new1 = x_initial + alpha1*S[0]

    # 沿坐标轴2的方向进行一维搜索
    f2 = f.subs({x1:(x_new1+alpha*S[1])[0],x2:(x_new1+alpha*S[1])[1]}).evalf()
    alpha2 = solve(diff(f2,alpha),alpha)[0]
    x_new2 = x_new1 + alpha2*S[1]

    # 构造共轭方向
    S1 = np.array(x_new2-x_initial)
    # 沿共轭方向进行一维搜索
    f3 = f.subs({x1:(x_new2+alpha*S1)[0],x2:(x_new2+alpha*S1)[1]}).evalf()
    alpha3 = solve(diff(f3,alpha),alpha)[0]
    x_new3 = x_new2 + alpha3*S1
    x_point.append([x_initial,x_new1,x_new2,x_new3])
    
    
    # 精度判断--满足精度要求即可退出函数 
    if math.sqrt(sum([i**2 for i in (x_new3-x_initial)])) <= epsilon:
        f_min = f.subs({x1:x_new3[0],x2:x_new3[1]})
        # 为了绘图方便将其转为ndarray
        x_point = np.array(x_point)
        print('最优解为：',x_new3)
        print('最优值为：',f_min)
        print('迭代次数为：',k)
        #print('迭代轨迹为：',x_point)
        return None
      
    # 递归调用函数
    k += 1 # 迭代次数加1
    x_initial = x_new3
    S = np.array([S[-1],S1])
    Powell(f,x1,x2,epsilon,k,S,x_initial,x_point)

# 构造函数表达式
x1 = sp.Symbol('x1')
x2 = sp.Symbol('x2')
f = (x1+x2)**2+(x1-1)**2
display(f)

# 初始化参数
k = 0
S = np.array([[1,0],[0,1]])
epsilon = 0.001
x_initial = np.array([2,1])
x_point = list()
Powell(f,x1,x2,epsilon,k,S,x_initial,x_point = x_point)

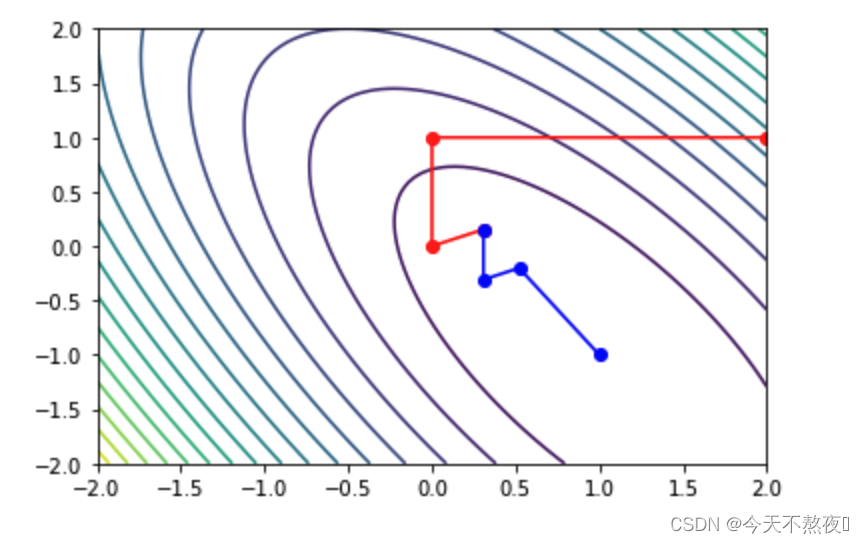
# 可视化
def plt_contour(f,x1,x2):
    f = sp.lambdify([x1,x2],f,'numpy')
    x1 = np.linspace(-2,2,100)
    x2 = np.linspace(-2,2,100)
    X1,X2 = np.meshgrid(x1,x2)
    Z = f(X1,X2)
    fig = plt.contour(X1,X2,Z,20)
    return fig
fig = plt_contour(f,x1,x2)
# 第一次
plt.plot([x_point[0][i][0] for i in range(len(x_point[0]))],
         [x_point[0][i][1] for i in range(len(x_point[0]))],
         marker = 'o',color = 'r')
# 第二次
plt.plot([x_point[1][i][0] for i in range(len(x_point[1]))],
            [x_point[1][i][1] for i in range(len(x_point[1]))],
            marker = 'o',color = 'b')