无约束优化方法----改进的Powell法

最新推荐文章于 2024-11-28 15:32:32 发布

今天不熬夜⁠

最新推荐文章于 2024-11-28 15:32:32 发布

阅读量1.1k

点赞数 3

分类专栏：优化设计文章标签： python numpy 数学建模

本文链接：https://blog.csdn.net/weixin_53356632/article/details/130767144

版权

文章介绍了改进的Powell法，即修正的共轭方向法，与原始Powell法的区别在于其迭代过程。提供了一个使用Python实现的示例，包括一维搜索、终止条件以及反射点和共轭方向的计算。此外，还展示了如何用numpy和sympy库进行数值优化，并给出了可视化移动轨迹的方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

改进Powell法的Python实现

上一次介绍了Powell法的迭代步骤、对应例题的Python实现。本节介绍改进Powell法（修正的共轭方向法）。

1. 改进的Powell法

改进Powell法与Powell法最大的区别主要在于：
在这里插入图片描述

1.1 Powell法的计算流程

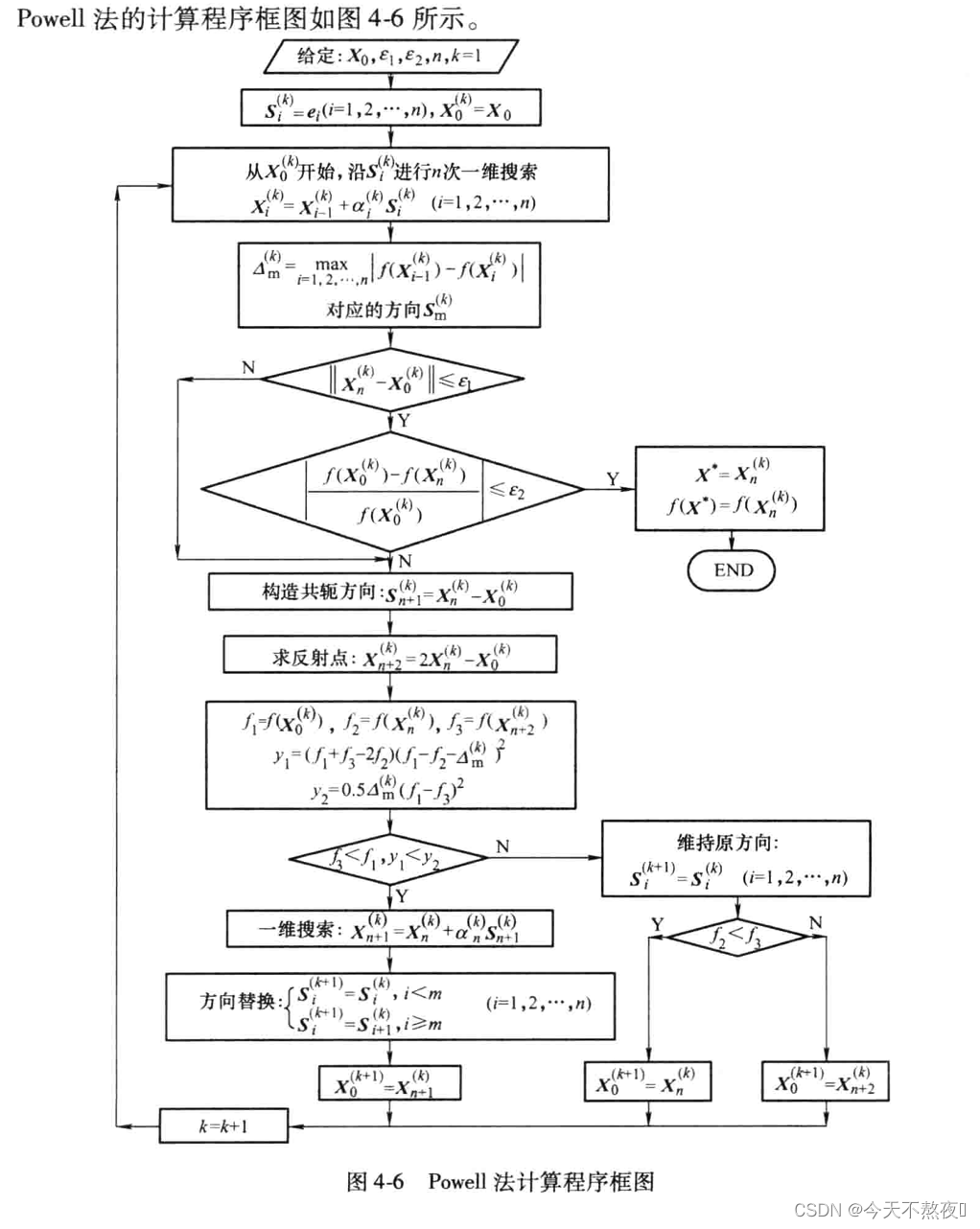
在这里插入图片描述

1.2 例题

在这里插入图片描述

1.2.1 Python实现：

import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
from sympy import *

def Powell_modified(x_0,fun,x,f_np,n,epsilon1,epsilon2,S,x_point,k=0): 
    
    # 从初始点开始进行n次一维搜索
    x_new = np.zeros((n,len(x_0)))
    lambd = symbols('lambd')
    delta_m = np.zeros(n)
    x_initial = x_0.copy()
    for i in range(n):
        
        x_n = x_initial + lambd*S[i]
        f_lambd = fun.subs({
   x[j]:x_n[j] for j in range(len(x_n))})
        lambd_value = solve(diff(f_lambd,lambd),lambd)
        x_new[i] = x_initial + lambd_value[0]*S[i]
        delta_m[i] = abs(f_np(*[x_initial[j] for j in range(len(x_initial))])-f_np(*[x_new[i][j] for j in range(len(x_new