（精读）二元传染和Ising数据的单纯复形完全重构

卜茶茶

已于 2024-05-24 01:10:31 修改

阅读量500

点赞数 5

分类专栏：文献阅读文章标签：重构

于 2024-05-09 22:39:37 首次发布

本文链接：https://blog.csdn.net/weixin_53406075/article/details/138283998

版权

文献阅读专栏收录该内容

4 篇文章 0 订阅

订阅专栏

文献翻译，帮助自己好理解，不另作他用。（其中很多基础知识和图片摘自网络）

文章原标题为：Full reconstruction of simplicial complexes from binary contagion and Ising data

原文链接：

Full reconstruction of simplicial complexes from binary contagion and Ising data | Nature Communicationshttps://www.nature.com/articles/s41467-022-30706-9

泊松分布的“入"最大似然估计 - CreatorKou - 博客园 (cnblogs.com)

期望最大化（EM）算法：从理论到实战全解析 - 知乎 (zhihu.com)

最大似然估计基本原理及数学推导摘自公众号：控我所思制之以衡

摘要

以前基于数据的重建工作主要集中在具有成对或两体相互作用的复杂网络上。人们对具有高阶或多体相互作用的网络越来越感兴趣，提出了基于观测数据重建此类网络的需求。我们基于两种类型的离散状态动力学的二进制时间序列数据，开发了一个结合统计推理和期望最大化的一般框架，以完全重构两体和三体相互作用的2-单纯复形。我们进一步阐明了一个两步方案，以提高重建精度，同时显著减少计算负荷。通过合成的和真实的2-单纯复形，我们验证了该框架，证明了所有的连接都可以被真实地识别出来，并且可以推断出2-单纯复形的完整拓扑。并且本文研究了噪声数据或随机干扰的影响，证明了所提框架的鲁棒性。

正文

在网络科学与工程中，从数据中寻找网络拓扑结构和节点动力学方程是研究的一个分支领域。这一点很重要，因为网络在现实世界中无处不在，但它们的连接拓扑和控制网络属性和物理可观察性的内在动力系统的细节通常是未知的。这些细节不仅是为了理解，也是为了保护、禁用或控制网络动态行为(取决于具体的应用)，一个可行的方法是解决通过可用的观测数据确定网络细节的逆问题。对于数学和物理科学中的反问题，网络反问题都是具有挑战性的。这一领域以前的工作主要集中在“传统”网络上，只有成对相互作用。现有的方法包括基于驱动响应、自适应同步、噪声相关、压缩感知、最大似然估计和格兰杰因果关系的方法。数据可以来自连续时间或离散时间的动态过程。例如，驱动响应和自适应同步方法使用来自连续时间非线性耦合系统的数据，而最大似然估计方法适用于来自离散时间动态系统的数据。在本文中，由于高阶网络已经成为网络科学研究的一个最先进的子领域，我们开发了一个重建框架，用于从时间序列数据中寻找具有高阶相互作用的网络拓扑。

虽然两两或节点对节点的交互是网络中常见的类型，但人们已经认识到，高阶交互也无处不在，而且很重要。

为什么高阶交互很重要？例如，在社交网络中，在说服个人购买新产品方面，多个朋友的集体推荐往往比单个朋友的推荐更有说服力。在谣言传播过程中，如果一条虚假新闻被许多人同时分享或传播，它很可能被个人接受。类似的情况也发生在神经元网络中，其中放电事件通常是许多神经元之间兴奋性和抑制性相互作用的结果。

在所有这些情况下，相互作用在网络中的一组节点之间同时出现，用传统的成对相互作用来描述网络已不再足够，必须考虑超越成对关系的高阶相互作用。在数学上，高阶相互作用可以被描述为超图或单纯复形，即包含高阶简单体的网络。

k-单纯形描述了(k + 1)个节点之间的同时交互，其中0 -单纯形指定了一个孤立的节点(即没有任何交互)，1-单纯形表示传统的两两交互，2-单纯形表示三个节点之间的同时交互等等。

过去三年来，人们对高阶网络的兴趣日益浓厚。例如，（超图）研究了超图上的随机游走，其中行走者根据共享超边的数量和大小选择下一个目的地。在超图上构造了一组随机游走，其参数可以控制动力学对大小超边的偏向，并阐明了游走策略和游走时间对群落检测的影响。建立了超图上一般动态过程的稳定性条件，并构造了一个具有一阶和二阶跃迁、双稳性和滞后性等动力学现象的超图社会传染模型。（单纯复形）提出了一个简单的社会传染模型，并证明了2-单纯形中的强化机制可以导致不连续的相变。本文分析了单纯复形的异质性对具有集体和个体传染的SIS(易感-受感染-易感)传播模型的影响，并提出了一个研究单纯复形中SIS动力学的节点对逼近理论，认为该理论比马尔可夫链和平均场方法更准确。提出了一种在单纯复形中包含思想整合和信息传递的社会传播模型，并确定了导致信息爆发的关键条件。提出了一个简单的活动驱动模型，并分析了简单和时间演化相互作用的影响。在网络重建方面，最近开发了一种从成对链接的网络数据中检测高阶相互作用的统计方法。

在本文中，我们开发了一个框架来重建具有高阶交互的复杂网络。具体地说，我们关注具有2-单纯复形的网络，并假设网络上的动态过程是生成二进制时间序列数据的社会传染模型和简化伊辛模型。

（1）方法：基于最大似然估计的统计推断类型

（2）目的：同时完全重建成对交互和2-单纯复形，将我们的工作与最近基于链接数据的方法区分开。

（3）中心任务：估计每个节点连接到重建或目标节点(成对交互)的概率，以及任意两个节点与目标节点形成三体（2-单纯形）的概率。

（4）改良：提出了一个两步过程，大大提高了计算效率，并提出了一个有效的截断过程，以确定单纯复形的最终重建结构。

（5）验证：利用3个合成单纯复形和4个真实单纯复形，我们证明了我们的重建方法的准确性，并建立了它对网络平均程度和随机波动变化的鲁棒性。我们的工作代表了基于观察到的时间序列数据重建具有高阶相互作用的复杂网络的初步努力。

结论

一、单纯复形

二、社会传染动力学

同伴影响和强化机制在社会传染的动态过程中无处不在，网络中的高阶互动由此产生。提出了一种考虑2-单纯复形强化的社会传染模型，该模型利用SIS型带有二元状态动态变量的传播动力学。

三、简化伊辛动力学

伊辛模型由于其在统计物理相变中的基本作用而在许多领域出现。它也被应用于许多社会制度。虽然网络上的Ising动力学已经得到了广泛的研究，但以前的研究仅针对具有成对相互作用的网络进行。据我们所知，还没有研究过具有高阶相互作用的网络上的Ising动力学。

Ising模型的提出是为了解释铁磁物质的相变，即磁铁在加热到一定临界温度以上会出现磁性消失的现象，而降温到临界温度以下又会表现出磁性。这种有磁性、无磁性两相之间的转变，是一种连续相变（也叫二级相变）。

Ising模型假设铁磁物质是由一堆规则排列的小磁针构成，每个磁针只有上下两个方向（自旋）。相邻的小磁针之间通过能量约束发生相互作用，同时又会由于环境热噪声的干扰而发生磁性的随机转变（上变为下或反之）。涨落的大小由关键的温度参数决定，温度越高，随机涨落干扰越强，小磁针越容易发生无序而剧烈地状态转变，从而让上下两个方向的磁性相互抵消，整个系统消失磁性，如果温度很低，则小磁针相对宁静，系统处于能量约束高的状态,大量的小磁针方向一致,铁磁系统展现出磁性。而当系统处于临界温度的时候，Ising模型表现出一系列幂律行为和自相似现象。

为了解决2-单纯形的协同强化效应，我们在2-单纯复形上定义了一个简单的伊辛动力学。每个节点有两种可能的状态:自旋向下( $S{_{i}^{t}}=+1$ )或自旋向上( $S_{i}^{t}=-1$ )。初始时刻，每个节点 $i$ 的状态随机分配为 $+1$ 或，概率相等。将哈密顿函数定义为:

其中， $J_{1}$ 和 $J_{2}$ 分别为二体和三体相互作用的强度， $\left ( i,j \right )$ 和 $\left ( i,j,k \right )$ 分别为2-单纯复形中的二体和三体连接。哈密顿量的第一项描述了边之间的相互作用(即两体连接)，第二项包含了来自2-单纯形的三体相互作用。在每个时间步长，每个节点 $i$ 的自旋翻转概率（根据反转概率生成二进制时间序列）由 $f_{i}\left ( t+1 \right )=\left ( 1+e^{\delta \Delta E_{i}^{t}} \right )^{-1}$ 给出，其中 $\delta$ 为逆温度。

表示节点 $i$ 在时刻 $t$ 翻转引起的能量变化，其中 $\partial _{i}$ 和 $\bigtriangledown _{i}$ 分别是包含节点 $i$ 的1-单纯形集和2-单纯形集。

四、统计推断框架

对于发生在大小为N的2-单纯复形上的SIS和Ising过程，表示节点在不同时间步长状态的可用时间序列数据可以存储在数据矩阵S中，其中每一行是表示该时间步长所有节点状态的时间字符串，每一列是一个节点在不同时间步长的状态。我们用统计推理框架从数据矩阵S重构了2-单纯复形。该任务包括三个步骤:

(1)基于可用数据矩阵S建立似然函数;

(2)根据期望最大化(EM)方法的思想，通过最大化似然函数获得二体和三体相互作用的连接概率;

(3)执行改进的两步重建策略，显著提高计算效率。

五、重构性能的量化

机器学习中真假阳性的定义：

真阳性True Positive :实际为真，预测也为真，即正样本被正确识别的数量。

真阴性True Negative:实际为假，预测也为假，即负样本被正确识别的数量。

假阳性False Positive :实际为假，预测为真，即误报的负样本数量。

假阴性False Negative:实际为真，预测为假，即漏报的正样本数量。

TP+FN：真实正样本的总和，正确分类的正样本数量+漏报的正样本数量。

FP+TN：真实负样本的总和，负样本被误识别为正样本数量+正确分类的负样本数量。

TP+TN：正确分类的样本总和，正确分类的正样本数量+正确分类的负样本数量。

第一个词代表是否预测正确：真正的XX或者错误的XX！

第二次词代表预测结果如何：XX的正例（阳性）或者XX的负例（阴性）。

本文中使用F1分数来量化重建精度，这是一个全局性能指标，定义为 $F1=\frac{2P*R}{P+R}$

其中 $P=\frac{TP}{TP+FP}$ 、 $R=\frac{TP}{TP+FN}$ 。（F1的确定？）

更大的F1值对应的精度更高，F1 = 1表示原始网络结构已经完全重构，误差为零。

六、重建合成和现实世界的单纯复形

ERSC随机单纯复形；SFSC无标度单纯复形；SWSC小世界单纯复形

图1展示了重建三个合成2-单纯复形的结果，其中正方形、菱形和圆形表示重建两体连接的性能，而不同方向的三角形表示重建三体连接的性能。从图1可以看出几个特征。1、重构精度随着时间序列长度T的增加而增加，在T≥8000时可以达到单位值。2、二体和三体简单体的平均度k1和k2对重建精度的影响不同。特别是如图1a-c所示，k1值越小，两类简单体的重建精度越高。这可以通过k1的值越小意味着需要重建的两体连接越少来理解，从而提高了相同时间序列长度的两体连接的精度。同时，较少的二体连接减少了重建三体连接的复杂性，从而提高了重建精度。对于k2的影响，从图1d-f可以看出，k2的取值仅影响三体连接的重建精度，对2-单纯复形中不依赖于三体连接的两体连接的重建精度影响不大。3、由于三体相互作用的复杂结构及其对二体相互作用的依赖性，三体相互作用的重建精度低于二体相互作用。

图2显示了重建四个现实世界的2-简单复合体的结果:Hypertext200948, Thiers1249, InVS1550和lyonschool51,52。由数据集构建的2-单纯复形的基本参数如表1所示。由图2可以看出，对于现实世界的网络，无论是二体相互作用还是三体相互作用的重建精度都随着时间序列的长度而增加。值得注意的是，这些网络结构非常不规则，使重建变得复杂。然而，当T = 20,000时，F1得分可以超过80%。

一个具有实际意义的问题是我们的重建框架对随机扰动的鲁棒性。为了解决这个问题，我们在数据矩阵S中随机翻转感染状态的一小部分 $f$ 和相同数量的易感状态，并研究 $f$ 对以 $F1$ 为特征的重建精度的影响。三种合成的2-单纯复形和三种真实的2-单纯复形的结果如图3所示。可以看出，增加翻转的分数 $f$ 会导致 $F1$ 的减小。特别是，即使30%的感染状态被翻转( $f=0.3$ )，两体连接的 $F1$ 值也可以高达50%，证明了我们的框架在针对数据随机波动重建成对链接时的鲁棒性。

讨论

“网络结构”主要是指以网络的邻接矩阵为特征的成对连接的集合。由于目标是确定任意两个节点之间是否存在联系，现有的方法侧重于适合确定“两体”相互作用，例如基于成对相关或同步。从时间序列数据中找到复杂网络中高阶连接的问题尚未得到解决。

具有高阶连接的网络结构，也称为单纯复形，由高阶张量表示。例如，网络中的三体相互作用或2-简单体可以用秩为3的张量来描述。在结构上，单纯复形明显比只有成对连接的传统网络复杂，并且前者可以预期更丰富的动力学，这已经开始研究。从反问题的角度来看，从时间序列数据重构单纯复形是一个巨大的挑战。

本文专注于具有2-单纯复形的复杂网络，我们开发了一个统计推断框架，通过该框架，网络中的所有二体和三体相互作用可以同时从二进制时间序列数据中找到，即不需要关于要重建的网络的先验知识。我们的重建框架的主干是最大似然估计，它产生所有可能的成对和三体连接的概率，以及将概率与实际相互作用联系起来的标准。为了显著提高计算效率，我们提出并测试了两步法和截断法来确定简单配合物的真实结构。重建框架经受住了合成和现实世界单纯复形的准确性和对随机波动的鲁棒性测试。

未解决的问题：

（1）重建框架是根据来自社会传染动力学和简化Ising动力学的二进制时间序列数据制定的。如何从不同动态过程产生的数据中重构高阶网络是需要研究的问题。

（2）我们的统计推理方法是为2-单纯复形开发的，这可能是超越具有成对相互作用的传统网络的“最简单”网络结构。重建具有高阶相互作用的网络，如3-单纯复形和超图，是值得研究的。

（3）在较短的时间序列中，有必要研究提高重建精度的方法。

方法

一、统计推断框架的细节（以SIS为例)

我们通过一个说明性的例子来描述统计推断框架的细节，如图4所示，其中展示了一个N = 30个节点的2-单纯复形及其数据矩阵，分别在图4a、b中。对于这样一个承载SIS动态的网络，易感节点 $i$ （即 $S_{i}^{t}=0$ ）被感染的概率（即 $S_{i}^{t}=1$ ）仅由被感染的邻居和被感染的2-单纯形决定，其中2-单纯形中的另外两个节点在时间 $t$ 都被感染。从感染状态到易感状态的转换概率不依赖于邻居的状态。因此，构建网络只需要考虑从易感状态到感染状态的转移概率。我们强调，假设感染概率 $\beta _{1}$ 和 $\beta _{2}$ 以及恢复概率 $\mu$ 等动力学过程的细节是未知的，只有节点状态的二进制时间序列是可用的。图4给出了一个说明性的示例来描述我们方法的细节。

1、建立似然函数

思想：通过统计推断的方法将此问题转化为了似然函数最大化问题，即借助条件概率公式，可写出个体 i 的状态翻转是由其余任意单个个体激发的概率以及任意两个个体的协同强化而激发的概率，然后根据每一时间步中翻转次数的期望即可得到个体 i 在所有时间段被感染次数的似然函数。

让 $j\rightarrow i$ 表示节点 $j$ 对节点 $i$ 的状态有直接的影响。例如,节点 $j$ 可以直接传播病毒或发送的信息给节点 $i$ ，这意味着节点 $j$ 是节点 $i$ 的直接邻居节点之一。节点 $i$ 和 $j$ 从而形成1-单纯形，独立于时间 $t$ 的一个属性。同样,让 $j,k\rightarrow i$ 表示来自节点 $j$ 和 $k$ 的协同强化效应对节点i状态有直接影响的事件，它也与 $t$ 无关。在下文中，我们确定节点 $i$ 和节点 $j$ 连接的概率，以及三个节点 $i,j,k$ 形成三体连接 $\left ( i,j,k \right )$ 的概率。

在给定 $S_{j}^{t}=1$ 和 $S_{i}^{t}=0$ 的情况下， $S_{i}^{t+1}=1$ 和 $j\rightarrow i$ 的条件概率可以写成

$P_{j\rightarrow i}=P\left ( j\rightarrow i | S_{i}^{t}=0,S_{j}^{t}=1,S_{i}^{t+1}=1 \right )$ 为节点 $i$ 在条件 $S_{i}^{t}=0,S_{j}^{t}=1,S_{i}^{t+1}=1$ 下被节点 $j$ 感染的概率， $P_{j\rightarrow i}> 0$ 意味着节点 $j$ 是节点 $i$ 的邻居； $P_{j}^{i}=P\left ( S_{i}^{t+1}=1 |S_{i}^{t}=0,S_{j}^{t}=1 \right )$ 是在 $S_{i}^{t}=0,S_{j}^{t}=1$ 的条件下 $S_{i}^{t+1}$ 的概率，可以通过矩阵 $S$ 计算出来。（图中绿框和蓝框展示了例子）

在给定 $S_{j}^{t}S_{k}^{t}=1$ 和 $S_{i}^{t}=0$ 的情况下， $S_{i}^{t+1}=1$ 和 $jk\rightarrow i$ 的条件概率可以写成

根据式3,4，在 $t_{m}+1$ 时刻易感节点 $i$ 被感染的期望数量为

其中 $\Psi _{j}^{t_{m}}$ 表示节点 $j$ 在 $t_{m}$ 时刻被感染的事件， $\Psi _{jk}^{t_{m}}$ 表示节点 $j$ 和 $k$ 在 $t_{m}$ 时刻被感染的事件，取值为0或者1， $\varepsilon _{i}$ 表示由采集数据误差引起的噪声。

一般来说，给定数量的事件在固定时间间隔内发生的概率由泊松分布表征，因此我们使用泊松分布来捕捉节点i被感染时间的随机性。泊松分布的一个优点是可以用EM算法进行数学分析和计算。具体来说，似然函数可以描述为

2、基于EM算法的似然函数最大化

思想：根据EM方法的思想，进而估计出每个节点与重构节点构成两体的概率及任意两个节点与重构节点构成三体的概率。我们使用EM方法最大化似然函数，以确定Eq. 6中的参数Θ。对式6取对数形式，得到

将Jensen不等式应用于方程7右侧的对数项，得到

然后将Eq. 7的最大化问题转化为最大化下式:即（8）代入（7）中

将12式分别对 $P_{j\rightarrow i}$ ， $P_{jk\rightarrow i}$ ， $\varepsilon _{i}$ 求偏导

方程(Eqs. 9-11)和式(Eqs. 16-18)可用于求解 $P_{j\rightarrow i}$ ， $P_{jk\rightarrow i}$ ， $\varepsilon _{i}$ 。特别地，将这三个参数初始化为1，然后计算公式9-11中的 $\rho _{j}^{t_{m}}$ ， $\rho _{jk}^{t_{m}}$ ， $\rho _{\varepsilon _{i}}^{t_{m}}$ 的值，将它们代入公式16-18中，求出 $P_{j\rightarrow i}$ ， $P_{jk\rightarrow i}$ ， $\varepsilon _{i}$ 的值。我们重复这个过程，直到达到收敛。由于单次迭代过程不能保证全局优化，所以我们将上述迭代过程进行多次，并选择适当的值，使Eq. 12中的数量达到最大值。

例如，如图4c所示，根据此迭代过程给出 $P_{j\rightarrow 13}$ 和 $P_{jk\rightarrow 13}$ 的值，其中 $P_{j\rightarrow 13}$ > 0，并给出 $P_{jk\rightarrow 13}$ 的前10个值。同样，对于每个节点i，可以计算出 $P_{j\rightarrow i}$ 和 $P_{jk\rightarrow i}$ 的所有值。如图4d所示，横坐标上方的每一列对应于一个节点预测的1-单纯形概率(图4d的左子图)和2-单纯形概率(图4d的右子图)，蓝点和红点分别表示实际的和不存在的两体或三体连接。

3、改进的两部重建策略

思想：理论上来讲，通过对概率值截断后即可以得到重构结果。然而，不难发现仅利用前两步进行重构的效率非常低，其复杂度主要来源于对于2-单纯形的预测，因为在预测每个节点所属的2-单纯形时，都需要计算出 $\binom{n-1}{2}$ 的概率值。利用单纯复形自身的性质，提出了一种改进的两步走重构策略，即首先预测出每个节点的“近似”邻居，并提取出预测邻居的时间序列；然后仅基于提取出的时间序列，即可进一步高效预测出每个节点所属的两体及三体交互。（因为简单复合体的特殊性决定了与节点i构成2-单纯形的另外两个节点必须是节点i的邻居，因此如果节点j或节点k不是节点i的邻居，则不需要计算Pjk→i的概率。）

重构过程可以分为两步。第一步，预测每个节点的“近似”邻居·，并提取其在数据矩阵S中的对应列，得到压缩的数据矩阵。第二步，基于压缩后的数据矩阵，通过迭代式9-11和16-18，预测每个节点i的 $P_{j\rightarrow i}$ 和 $P_{jk\rightarrow i}$ 的值。我们的两步方法不是为一般具有挑战性的任务而设计的，即始终如一地推断任意高阶单纯复形的所有子面。实际上，我们的方法需要单纯复合体的闭合条件:需要事先知道重构的网络是一个2-单纯复合体。在此前提下，两步策略首先从推断的两体相互作用中推断出两体相互作用，然后推断出三体相互作用(即2-单纯形)。两步法是重建2-简配合物的一种有效方法，但目前的方法还不够成熟，不能用于重建超图，因为它的第二步是从邻居(即边)中找到三角形。在第一步中，由于忽略了三体相互作用，预测的邻体并不准确。实际上，这一步的主要目的是确定邻居的近似范围，以减少计算 $P_{jk\rightarrow i}$ 的时间。在不考虑三体相互作用的情况下，在tm + 1时刻被感染的易感节点的期望数量可以简单地表示为

其中记号 $P_{j\rightarrow i}^{0}$ 用来强调节点j只是节点i的“近似”邻居。假设节点i在每个时间段内被感染的次数Ψi服从泊松分布，我们得到似然函数为

用EM方法最大化似然函数，得到

同样通过迭代得到收敛后的参数估计值。值得注意的是， $P_{j\rightarrow i}^{0}$ 是一个概率，我们需要确定重建节点的“近似”邻居。理论上，“近似”邻居可以通过测试 $P_{j\rightarrow i}^{0}$ 是非零的。然而，由于噪声或与假设的偏差，实际上这是不可行的。例如，如图4f所示，即使 $P_{6\rightarrow 13}^{0}=0.0002$ 和 $P_{14\rightarrow 13}^{0}=0.0006$ ，节点6和14也不是节点13的邻居。为了克服这个困难，我们提出了一种截断方法来确定节点i的邻居，如下所示。

首先，请注意，当预测的邻居较少时，第二步的时间复杂度可以显著降低，但是预测的邻居太少会导致丢失邻居。相反，过多的邻居会增加时间复杂度。一种解决方案是使用合理的截断来确定每个节点的“近似”邻居。为此，我们重新排序概率 $P_{j\rightarrow i}^{0}$ 按降序排列，并在最大间隙中放置一个阈值Δi:

接下来，我们再次使用公式26来找到一个小于Δi的新阈值 $\bar{\Delta}_{i}$ 。最后，当 $P_{j\rightarrow i}^{0}> \bar{\Delta}_{i}$ 时，节点j被视为节点i的“近似”邻居。截断方法可以保证检测到所有的真实邻居和2-单纯体。（阈值的确定？）

一旦获得节点i的“近似”邻居，就可以提取这些邻居的时间序列(图4f, g)。节点i及其2-单纯形的邻居可以基于第二步快速重新预测，即基于压缩数据矩阵迭代公式9-11和公式16-18。例如，节点13的预测结果如图4h所示，其中各节点的 $P_{j\rightarrow i}$ 和 $P_{jk\rightarrow i}$ 的情况如图4i所示。然后可以根据图4i的结果确定每个节点的实际二体和三体连接。

因为在第二步中对两体连接的识别进行了细化，所以如果 $P_{j\rightarrow i}$ > 0，我们简单地假设节点j是节点i的邻居。根据前面的工作，我们假设节点i和j在 $P_{j\rightarrow i}>0$ 或 $P_{i\rightarrow j}>0$ 时连接。三体相互作用的情况更为复杂，解对噪声或误差敏感。事实上，使用条件 $P_{jk\rightarrow i}>0$ 作为检测(i, j, k)为2单纯形的标准可能会导致许多误报。我们的解决方案是重新排序 $P_{jk\rightarrow i}$ ，并通过再次使用Eq. 26获得新的阈值 $\hat{\Delta }_{i}$ 。因此，当 $P_{jk\rightarrow i}\geq \hat{\Delta }_{i}$ 时形成一个实际的2-单纯形(i, j, k)。为了消除预测中的冲突，我们假设当至少满足三个条件中的两个时便存在一个2-单纯形(i, j, k)，例如， $P_{jk\rightarrow i}\geq \hat{\Delta }_{i}$ , $P_{ik\rightarrow j}\geq \hat{\Delta }_{j}$ ，和 $P_{ij\rightarrow k}< \hat{\Delta }_{k}$ ，但当 $P_{jk\rightarrow i}\geq \hat{\Delta }_{i}$ ， $P_{ik\rightarrow j}< \hat{\Delta }_{j}$ 和 $P_{ij\rightarrow k}< \hat{\Delta }_{k}$ 同时存在时不存在2-单纯形。采用两步策略，我们可以重构整个二简复合体。如图4a所示，2-单纯复形得到了精确的重构。总的来说，两步策略不仅大大减少了计算时间，而且显著提高了重建精度。

二、合成的和现实世界的2-单纯复形的构造

随机单纯复形(ERSC):首先，以概率 $p_{1}$ 连接任意两个节点生成一个随机图。然后，我们以概率 $p_{2}$ 在任意三个节点之间添加2-simplexes，其中p1和p2的公式为:

然后可以使用概率 $p_{1}$ 和 $p_{2}$ 构造具有指定平均度的随机2-单纯复形。

SFSC (Scale-free simplisimplicomplex)（无标度单纯复形）:首先，生成一个无标度网络，其中每个新节点将m条边连接到具有度偏好的旧节点（高度节点）。然后，我们根据公式28中的概率 $p_{2}$ 在任意三个节点之间添加2-单纯形。1-单纯形的平均度可以计算为

小世界单纯复形(SWSC):首先，从一个规则晶格(所有节点都有相同的度2m)生成一个小世界网络，其重新布线的概率为p。然后，我们根据公式28中的概率 $p_{2}$ 在任意三个节点之间添加2-单纯复形。1-单纯复形的平均度数由式29给出。

来自真实世界数据的2-单纯复形。在每个真实世界的数据集中，面对面的相互作用以20秒的时间分辨率进行了测量。首先，我们根据数据生成一个加权网络，其中权重表示在整个时间窗口内一对节点之间的交互次数。其次，我们删除任何权重小于给定阈值ζ的链接，并将保留链接的权重设置为1，以生成一个未加权的网络。最后，我们以5分钟的时间窗口将数据分割成多个片段，并记录所有的2-单纯体。特别是，如果三个节点在短时间内相互通信，则认为它们构成了三体连接。我们记录每个片段中2-单纯形的频率。根据所有片段的总频率，我们保留频率最高的前50%的2-单纯形，并将其计数为实际的2-单纯形。图2a-d显示了四个现实世界的2-简配合物的可视化。

补充信息

一、不同疫情条件下的重建精度

一般情况下，重建精度取决于疫情情况。在正文中，生成数据的参数值选择在流行阈值附近，即在三角驱动和边驱动的过渡附近。为了评估在其他机制下选择参数值对重建结果的影响，我们重点研究了两个量:重新标度的边传染性α和重新标度的三角形传染性ω，并研究了它们对二体和三体连接重建精度的影响。特别是，社会传染概率为 $\beta_{1}=\frac{\alpha }{k_{1}}$ 和 $\beta_{2}=\frac{\omega }{k_{2}}$ ，其中k1和k2分别是2-单纯复合体中两体和三体连接的平均程度。

不同的β1和β2值对重建结果的影响有显著差异。当β1或β2的值较大时，感染的节点较多，难以判断在重构中是哪些感染的节点将感染传播给了节点。相反，当β1和β2的值较小时，一个易感节点很难被其他节点感染，导致重建任务缺乏有用的数据。所以需要适当选择β1和β2的值，以达到可接受的重建精度。我们系统地研究了不同的参数设置(例如，根据重新标度的传染性α和ω)及其对重建精度的影响。

具体地说，我们研究了N = 200, k1 = 14, k2 = 4的无标度单纯复形(SFSC)。图S1显示了不同ω值下稳定状态下感染节点的ρ∗的平均分数。可以看出，随着ω的增加，潜在社会传染动态的相变性质从连续变为不连续。此外，感染节点密度ρ0的不同初始值会影响双稳态区域中与健康和地方病状态相关的稳态感染密度ρ *。（？）

然后，我们分别在边流行病阈值 $\alpha _{c}$ 以下、附近和上方选择3个不同的α值(0.5、0.8和1.5)，研究不同ω值对重建精度的影响。具体地说，我们选择ω = 0.8, 2.4和4.0，它们分别位于三角形流行病阈值 $\omega _{c}$ 的下方，附近和上方。1、图S2(a)显示，当α = 0.5时，二体和三体连接的重建精度不高，这是因为当重新标度的边传染性α较小时，单纯复形的社会传染难以传播。2、增大ω值可以提高重建精度。例如，如图S2(b)所示，对于α = 0.8且时间较长的序列，当ω = 2.4时，二体连接和三体连接的重建精度最高，因为ω值小意味着三体连接的协同增强作用不显著，而ω值大则会削弱两体连接的相互作用，特别是当α值接近边缘阈值时。这两种效应都会导致重建二体或三体连接的困难。3、图S2(c)显示，当α = 1.5时，ω = 2.4时二体和三体连接的重建精度一般高于其他两种情况，因为较小的ω值(如ω = 0.8)不能产生较强的三体连接的协同增强效应，而较大的ω值(如ω = 4)则会导致大多数节点被感染。综上所述，当α和ω值接近各自的流行阈值时，重建精度可能达到最高。

二、一步法与两步法的比较

为了比较一步法和两步法的精度和时间复杂度，我们使用了不同大小和平均度的无标度单纯复形(SFSC)。结果如图所示。S3和S4。特别是，从图S3可以看出，无论是二体重建还是三体重建，两步法的精度都要高于一步法。当网络规模较大时，两步法的优越性更加明显。图S4展示了这两种方法的运行时间，这两种方法是在MATLAB2016a中实现的，并在具有2.60 ghz Intel处理器、28个CPU内核和192 gb RAM的Linux机器上运行。可以看出，两步法所需的计算时间比一步法所需的计算时间低一个数量级以上。

三、从简化动力学重构2-简单配合物

（草稿，有点乱.....）

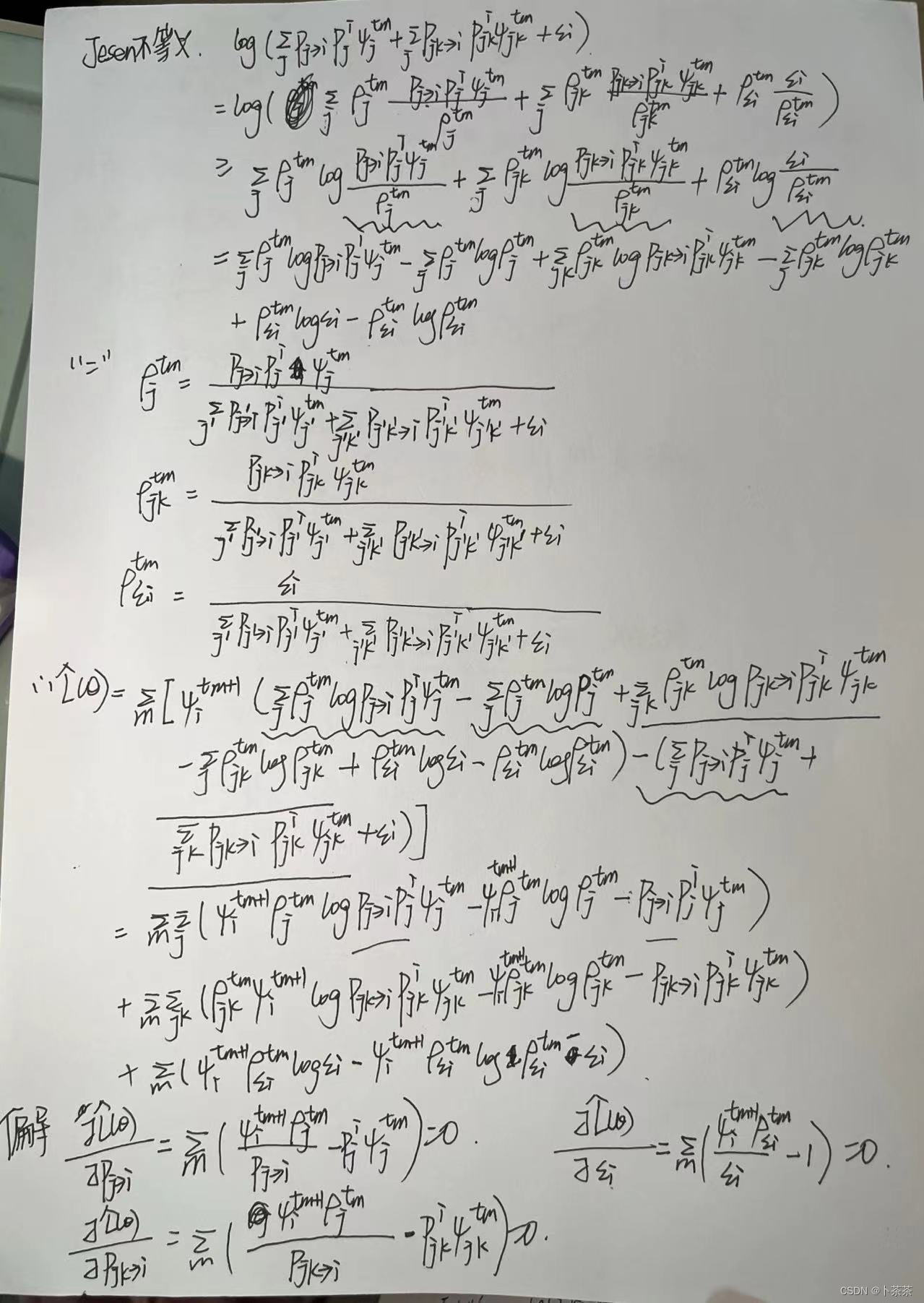
我们注意到，根据翻转概率 $f_{i}\left ( t+1 \right )=\left ( 1+e^{\delta \Delta E_{i}^{t}} \right )^{-1}$ ，在每个时间步长，无论邻居的状态如何，每个节点总是有一个或大或小的翻转概率，因此时间序列数据中总是存在噪声。因此，第二步的两体连接预测根据正文中的式(26)进行截断，而不是像社会传染动力学那样简单地从零开始。对于预测三体连接，可以使用与社会传染动力学相同的截断方法。

C、简化伊辛动力学的代表性重构结果

图S5和图S6分别显示了N = 100和N = 200时随机单纯复形(ERSC)、无标度单纯复形(SFSC)和小世界单纯复形(SWSC)的结果。图S7显示了四个现实世界的2-单纯复形的重建结果。
类似于从社会传染模型重构2-单纯复形的情况。图S5-S7表明，增加时间序列长度T可以提高二体和三体连接的重建精度。此外，较小的k1值往往会提高这两种简单体的重建精度。不同的k2值对重建精度影响不大。对于同样数量的数据，较大的网络通常会导致较低的精度。最后，二体连接的重建精度普遍高于三体连接。

四、以事件数量表示的重构性能

我们将F1分数作为无标度单纯复形(SFSC)(图S8)和四个现实世界的2-单纯复形(图S9)的事件数的函数，其中在每个节点上计算事件数。例如，100个事件意味着每个节点在易感状态和受感染状态之间有100个切换。可以看出，重构精度随着事件数量的增加而增加。此外，二体和三体连接的重建精度随k1(即1-单纯形的平均度)的增大而减小，而k2(即2-单纯形的平均度)的取值仅影响三体连接的精度，对二体连接的重建精度影响不大。虽然较大的单纯复形需要更多的事件才能达到一定的F1分数，但只要有足够的数据，仍然可以实现较高的重建精度。得出的结论是，基于事件数的结果与基于模拟时间T的结果基本相同。

五、信息测度

在最近的工作[2]中，引入了一个名为O-information (Ω)的重要信息度量，它可用于表征协同和冗余主导的系统，并量化高阶相互依赖性。由本文引理1（参考文献[2]中）可知，O-information只能捕捉到超出两两关系的相互作用，因此不适合描述两个变量的相互作用，即不能用来重构两两关系。
更具体地说，对于三个离散变量的系统，对于n = 3时，O-information定义为

根据该度量，当Ω(X3) > 0时，系统为冗余主导;反之(Ω(X3) < 0)，则为协同主导。为了将我们的方法与这种基于O-information的方法进行比较，我们计算了任意三个变量之间的O-information值。如果为负，则三个变量之间存在交互作用(三体连接)，否则不存在连接。结果如图S10所示，其中显示任意三个点的O-information值，其中蓝点表示存在三体连接，红点表示不存在三体连接。可见，大多数存在的三体相互作用的O-information值确实为负，但许多不存在的三体相互作用的o信息值也为负，使得无法区分两种情况，无法确定存在的三体相互作用。
总体而言，[PRE 100, 032305(2019)]中提出的O-information方法依赖于动态变量时间序列之间的强相关性来预测协同结构。在我们的例子中，动态时间序列数据是通过交替更新迭代获得的，即每个节点的状态转换是由相邻节点在前一时刻的状态决定的，导致任意时刻不同节点对之间只有弱相关性。因此，O-information方法不适合从动态时间序列数据中预测高阶结构。

六、时间序列长度对重建性能的影响

研究了不同噪声水平(翻转比)f: f = 0(无噪声)、0.1、0.2和0.3时，合成和现实2-单纯复形对时间序列长度T的重建性能，结果如图所示。分别是S11和S12。这些结果表明，对于短时间序列，重构性能对噪声敏感。
例如，当f的值从0变为0.1时，F1分数会有相当大的下降。无论噪声水平如何，增加时间序列长度总能提高二体和三体相互作用的重建性能。

卜茶茶

关注

5
点赞
踩
4

收藏

觉得还不错? 一键收藏
打赏
0
评论
（精读）二元传染和Ising数据的单纯复形完全重构

以前基于数据的重建工作主要集中在具有成对或两体相互作用的复杂网络上。人们对具有高阶或多体相互作用的网络越来越感兴趣，提出了基于观测数据重建此类网络的需求。我们基于两种类型的离散状态动力学的二进制时间序列数据，开发了一个结合统计推理和期望最大化的一般框架，以完全重构两体和三体相互作用的2-单纯复形。我们进一步阐明了一个两步方案，以提高重建精度，同时显著减少计算负荷。通过合成的和真实的2-单纯复形，我们验证了该框架，证明了所有的连接都可以被真实地识别出来，并且可以推断出2-单纯复形的完整拓扑。
复制链接

扫一扫