DFS解题

目录

递归

区分递归和递推

DFS的主要思想

DFS---凑算式问题（可以用next_permutation()）

蓝桥杯-三羊献瑞

蓝桥杯-凑算式

整数划分有多少种划分

​

 DFS 排列组合问题

---

递归

区分递归和递推

写递归的代码时，每一次调用函数只做一小件事，然后把剩下的工作传到新一次调用里

1.要找到每一次工作的相似性

2.不能相似的原因很可能是缺少参数，因为有时候不加一个参数，每次传的参数都无法发生变化，就会陷入死循环，栈溢出

3.注意递归的出口

几个常见的用递归能解的小题：

//字符串反转
string F(string s){
	if(s.size()==1)return s;
	return F(s.substr(1,s.size()-1))+s[0];
} 
int main(){
	string s="evol";
	cout<<F(s);
}

//求杨辉三角第m层的第n个数
int F(int m,int n){
	if(n==1)return 1;
	if(m==n)return 1;
	return F(m-1,n-1)+F(m-1,n);
} 
int main(){
	cout<<F(3,2);
}

//3个A,2个B一共有多少种排列组合
int F(int A,int B){
	if(A==0 || B==0)return 1;
	return F(A-1,B)+F(A,B-1);
} 

DFS的主要思想

使用栈保存未被检测的结点，结点按照深度优先的次序被访问并依次被压入栈中，并以相反的次序出栈进行新的检测

DFS解题时通常用到两个数组

• 一个用来标记该点是否被访问过
• 一个用来把该点放入

从一个走迷宫常用的解题模板引入：

const int maxn = 100;		//最大范围 
bool visit[maxn][maxn];		// 访问标记
int map[maxn][maxn];		// 坐标范围
int dir[4][2] = { 0,1,
				  0,-1,
				  1,0,
				  -1,0 }; // 方向向量，(x,y)周围的四个方向

bool Check(int x, int y) // 边界条件和约束条件的判断
{
	if (!visit[x][y] && ...) // 满足条件且此点没有被访问过
		return 1;
	else // 与约束条件冲突或者此点已经被访问过
		return 0;
}

void dfs(int x, int y)
{
	visit[x][y] = 1; // 标记该节点被访问过
	if (map[x][y] == G) // 出现目标G
	{
		...... // 做相应处理
			return;
	}
	for (int i = 0; i < 4; i++)
	{
		if (Check(x + dir[i][0], y + dir[i][1]))
         // 按照规则生成下一个节点，这样就试探了所有的情况
			dfs(x + dir[i][0], y + dir[i][1]);   
	}
	return; // 上边的递归已经运行完退出来了，回溯
}

下面整理一些遇到的典型的DFS题目类型

DFS---凑算式问题（可以用next_permutation()）

蓝桥杯-三羊献瑞

 思路：本题是一个典型的凑算式问题，一共有八个不可以重复的数，要让它们满足这个等式

一共8个数，从0~9中找——依次对应为a[0]~a[7]

不可以重复——设立visit数组，如果i已经放入a数组了，visit[i]=1

如何深度搜索——dfs的参数就写a[index]的下标index，找遍这8个数

递归退出的条件——找够了8个数且满足这个算式，这样也刚好与上边的深度搜索吻合了，

                                正因为index++,最终才会==8，得以退出递归

#include<iostream>
using namespace std;

int a[8];
bool visit[10];

void dfs(int index) {
	//退出条件
	if (index == 8) {
		if (
			(a[0] * 1000 + a[1] * 100 + a[2] * 10 + a[3]) +
			(a[4] * 1000 + a[5] * 100 + a[6] * 10 + a[1])
			== (a[4] * 10000 + a[5] * 1000 + a[2] * 100 + a[1] * 10 + a[7])
			) 
		{

			cout << a[4] << a[5] << a[6] << a[1];
			return;
		}
	}
	
	else {
		for (int i = 0; i <= 9; i++) {
			if (index == 0 && i == 0) continue;//不可能把0赋值给a[0]
			if (index == 4 && i != 1)continue;//a[4]必定==1
			//最精髓的地方
			if (visit[i] == 0) {   //如果0~9中这个数还没用过
				visit[i] = 1;		//现在用了
				a[index] = i;		//给当前这层递归的a[index]赋上这个还没用过的数
				dfs(index + 1);		//去下一层递归给a[index]赋一个值
				visit[i] = 0;		//之前的递归都退出后，相当于试完了一种情况，现在0~9又都能用了，开始新的一轮
			}
		}
	}
	
}

int main() {
	dfs(0);		//显然index从0开始
}

蓝桥杯-凑算式

 思路：和上边的题一模一样，上边是汉字对应数字凑算式，这个是字母对应数字

1.要a[9]

2.要visit[9]

3.深度靠index++

4.退出条件是找够9个且凑成了算式

5.一些微妙的不同，上边是输出，return，这个是计数，其实都一个道理

6.细节，这个题是1~9，而visit数组对应的下标是（1~9）-1

7.犯错的点，注意不管怎样都要return

#include<iostream>
using namespace std;

int a[9];
bool visit[9];
int cnt = 0;

void dfs(int index) {
	if (index == 9) {
		if (a[0] + a[1] / a[2] + (a[3]*100 + a[4] *10+ a[5]) / 
            (a[6] * 100 + a[7] * 10 + a[8]) == 10)
			cnt++;
		return;    //要么cnt++要么不加，但是最终一定要return的
	}

	else {
		for (int i = 1; i <= 9; i++) {
			if (visit[i-1] == 0) {
				visit[i-1] = 1;
				a[index] = i;
				dfs(index + 1);
				visit[i-1] = 0;
			}
		}
	}
}

int main() {
	dfs(0);		//显然index从0开始
	cout << cnt;
}

【关于为什么要回溯的理解】所有开关串联一盏灯，现在

有的开关开着有的开关没开，要试出怎样能点亮这盏灯——首先拉一个开关，拉下，不亮，要拉上去….直到试完所有的一个开关的情况

然后到了两个开关的试探，拉两盏灯，拉下，不亮，要拉上去再试新的

试探完一种情况，拉上去这个过程，就是递归中dfs结束后的回溯

但是在做了上面两道题之后，发现了next_permutation(a,a+n)函数......

需要头文件<algorithm>

next_permutation()的返回值：当当前序列不存在下一个排列时，返回false，否则返回true

next_permutation(num,num+n)函数是对数组num中的前n个元素进行全排列，同时并改变num数组的值

#include <iostream>  
#include <algorithm>  
using namespace std;  
int main()  
{  
    int num[3]={1,2,3};  
    do  
    {  
        cout<<num[0]<<" "<<num[1]<<" "<<num[2]<<endl;  
    }while(next_permutation(num,num+3));  
    return 0;  
}  

输出结果为：

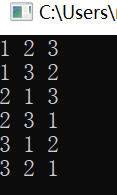
 需要强调的是，next_permutation（）在使用前需要对欲排列数组按升序排序，否则只能找出该序列之后的全排列数

于是...三羊代码变成

#include<iostream>
#include<algorithm>
using namespace std;

int a[10]={0,1,2,3,4,5,6,7,8,9};

int main() {
	do{
		if(a[4]==1 && 
            (a[0] * 1000 + a[1] * 100 + a[2] * 10 + a[3]) +
			(a[4] * 1000 + a[5] * 100 + a[6] * 10 + a[1])== 
            (a[4] * 10000 + a[5] * 1000 + a[2] * 100 + a[1] * 10 + a[7])
            )
            {
				cout << a[4] << a[5] << a[6] << a[1];
				break;
			}
			
		
	}while(next_permutation(a,a+10));
	
}

于是，凑算式代码变成

#include<iostream>
#include<algorithm>
using namespace std;

int a[9]={1,2,3,4,5,6,7,8,9};

int main(){
	int cnt=0;
	do{
		if (a[0] + a[1] / a[2] + (a[3]*100 + a[4] *10+ a[5]) / 
            (a[6] * 100 + a[7] * 10 + a[8]) == 10)
			cnt++;
		
	} while(next_permutation(a,a+9));
	cout<<cnt;
}

国赛里也有一道题是这样，w(ﾟДﾟ)w

 

那么，可以对字符串之类不是数的东西进行全排列吗？

void dfs(string s,int k){   //k代表当前关注点是字符数组中的第几位，这个参数挺常用的
	if(k==s.size()-1) cout<<s<<endl;
	for(int i=k;i<s.size();i++){
		swap(s[i],s[k]);    //把它后边所有的和它交换一次，试探
		dfs(s,k+1);
		swap(s[k],s[i]);  	//回溯 
	}
} 
int main(){
	dfs("abcd",0);
}

整数划分有多少种划分

 令n=m1+m2+...+mi;

(1)当n=1时，不论m的值为多少（m>0)，只有一种划分即{1};

(2)当m=1时，不论n的值为多少，只有一种划分即n个1，{1,1,1,...,1};

(3)当n=m时，根据划分中是否包含n，可以分为两种情况：

      (a)划分中包含n的情况，只有一个即{n}；

      (b)划分中不包含n的情况，这时划分中最大的数字也一定比n小，即n的所有(n-1)划分。 因此 q(n,n) =1 + q(n,n-1);

(4)当n<m时，由于划分中不可能出现负数，因此就相当于q(n,n);

(5)但n>m时，根据划分中是否包含最大值m，可以分为两种情况：

       (a)划分中包含m的情况，即{m, {x1,x2,...xi}}, 其中{x1,x2,... xi} 的和为n-m，因此这情况下为q(n-m,m)

       (b)划分中不包含m的情况，则划分中所有值都比m小，即n的(m-1)划分，个数为q(n,m-1);

      因此 q(n, m) = q(n-m, m)+q(n,m-1);
 

#include<iostream>
using namespace std;
int F(int n, int m) {
	if(n < 1 || m < 1) return 0;
	if(n == 1 || m == 1) return 1;
	if(n < m) return F(n, n);
	if(n == m) return F(n, m-1) + 1;

	return F(n, m-1) + F(n-m, m);
}
int main() {
	cout<<F(6, 6)<<endl;
	return 0;
}

 DFS 排列组合问题

【在n个球中任意取出m个不放回，求有多少种不同的取法】

这道题的核心思想是，当前这个球取还是不取？

取---->它的子问题是在剩下的n-1个中取m-1个

不取---->它的子问题是在剩下的n-1个中取m个

再写好出口条件，最后把取不取两种情况加起来就好

//在n个球里取m个 
int dfs(int n,int m){
	//dfs(n-1,m-1)的出口 
	if(m==0) return 1;
	//dfs(n-1,m)的出口 
	if(n==m) return 1;
	return dfs(n-1,m)+dfs(n-1,m-1); 
}

上边一道同理的题： 

//3个A,2个B一共有多少种排列组合
int F(int A,int B){
	if(A==0 || B==0)return 1;
	return F(A-1,B)+F(A,B-1);
}