7.Pandas 数据可视化图-2-CSDN博客

import matplotlib.pyplot as plt
import numpy as np

# 模拟数据（示例：正态分布）
data = np.random.randn(1000)  

plt.hist(
    x,  # 必选：数据（列表、数组等）
    bins=None,  # 分组数量/区间，核心参数
    range=None,  # 数据范围（元组，如 (min, max) ）
    density=False,  # 是否归一化为概率密度
    color='blue',  # 柱子颜色
    alpha=0.7,  # 透明度
    edgecolor='black',  # 柱子边框颜色
    linewidth=1.2,  # 边框宽度
    label='直方图',  # 图例标签
)
plt.legend()
plt.show()

关键参数详解

参数	作用与用法	示例
`x`	输入数据（1D 数组 / 列表），必选参数	`data = np.random.rand(100)`
`bins`	分组方式： - 整数：指定分组数量（如 `bins=10` ） - 数组：自定义分组区间（如 `bins=[0, 2, 5, 10]` ）	`bins=15` 或 `bins=[0, 1, 3, 6]`
`range`	限制数据范围，仅统计 `[min, max]` 内的数据，可截断异常值	`range=(0, 10)`
`density`	是否归一化： - `False`（默认）：Y 轴为频数（count） - `True`：Y 轴为概率密度（总和为 1）	`density=True`
`color`	柱子填充颜色（支持英文、十六进制等）	`color='#FF6347'` 或 `color='red'`
`edgecolor`	柱子边框颜色	`edgecolor='white'`
`alpha`	透明度（0 全透明～1 不透明），用于叠加图或突出对比	`alpha=0.5`

含多分组对比

# 两组模拟数据
data1 = np.random.normal(0, 1, 1000)  # 正态分布
data2 = np.random.uniform(-3, 3, 1000)  # 均匀分布

plt.figure(figsize=(8, 5))
# 绘制第一组
plt.hist(data1, bins=20, density=True, color='skyblue', edgecolor='black', alpha=0.7, label='正态分布')
# 绘制第二组（叠加，调整透明度）
plt.hist(data2, bins=20, density=True, color='orange', edgecolor='black', alpha=0.5, label='均匀分布')

plt.xlabel('数值')
plt.ylabel('概率密度')
plt.title('Matplotlib 直方图对比')
plt.legend()
plt.grid(axis='y', alpha=0.3)  # 加 Y 轴网格
plt.show()

1.1.2 Seaborn 实现（更简洁，适配 Pandas）

Seaborn 的 histplot 对直方图做了封装，支持直接传入 Pandas DataFrame，且默认集成核密度估计（KDE），更适合数据分析场景。

语法：

import seaborn as sns
import pandas as pd

# 构造 DataFrame（示例）
df = pd.DataFrame({
    'value': np.random.randn(1000),
    'category': np.random.choice(['A', 'B'], 1000)  # 分组类别
})

sns.histplot(
    data=df,  # 必选：DataFrame/Series
    x='value',  # 数据列（用于 X 轴）
    hue='category',  # 分组列（不同类别用不同颜色）
    bins='auto',  # 分组策略（auto 为自动优化）
    kde=True,  # 是否叠加核密度曲线
    stat='count',  # 统计量：count（频数）/ density（概率密度）/ probability（概率）/ proportion（比例）
    element='bars',  # 图形元素：bars（默认直方图）/ step（阶梯图）/ poly（多边形）
    palette='Set1',  # 配色方案
    alpha=0.6,  # 透明度
)

关键参数详解

参数	作用与用法	示例
`data`	输入数据（Pandas DataFrame/Series），必选（与 `x` 配合）	`data=df`
`x`	指定 DataFrame 中用于绘制直方图的列名（连续型数据）	`x='salary'`
`hue`	分组列名（离散型，不同分组用不同颜色区分）	`hue='gender'`
`bins`	分组方式： - 整数：指定分组数 - `'auto'`：自动优化分组（推荐） - 数组：自定义区间	`bins='auto'` 或 `bins=12`
`kde`	是否叠加核密度曲线（KDE），快速看分布形态	`kde=True`
`stat`	统计量类型： - `count`（默认）：Y 轴为频数 - `density`：概率密度 - `probability`：概率（总和为 1）	`stat='density'`
`element`	图形样式： - `'bars'`（默认）：标准直方图 - `'step'`：阶梯直方图 - `'poly'`：多边形填充	`element='step'`
`palette`	配色方案（Seaborn 或 Matplotlib 配色，如 `'Set2'`、`'tab10'` 等）	`palette='Pastel1'`

# 构造带分组的数据
df = pd.DataFrame({
    'score': np.concatenate([
        np.random.normal(60, 10, 500),  # 组 A：均值60，标准差10
        np.random.normal(70, 8, 500)    # 组 B：均值70，标准差8
    ]),
    'group': ['A']*500 + ['B']*500
})

plt.figure(figsize=(8, 5))
sns.histplot(
    data=df, 
    x='score', 
    hue='group',  # 按 group 分组，不同颜色
    bins='auto',  # 自动优化分组
    kde=True,     # 叠加核密度曲线
    stat='density',  # Y 轴为概率密度
    element='bars', 
    palette='Set2', 
    alpha=0.6
)
plt.xlabel('考试分数')
plt.ylabel('概率密度')
plt.title('Seaborn 分组直方图（含 KDE）')
plt.show()

直方图 vs 柱状图（避坑）

对比项	直方图（Histogram）	柱状图（Bar Plot）
数据类型	连续型数据（如身高、分数、时间）	离散型数据（如类别、名称、年份）
柱子含义	柱子宽度代表区间（连续），高度代表频率	柱子宽度无意义，高度代表类别数值
柱子间距	无间距（连续区间）	有间距（区分离散类别）
核心作用	展示数据分布形态（如正态、偏态）	对比类别间的数值大小

1.2 任务：分析所有顾客的总消费金额，观察不同消费水平的人数

1.2.1 数据准备

1.数据读取

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['axes.unicode_minus'] = False 
sns.set_style('whitegrid',{'font.sans-serif':['Arial','SimHei']})

df = pd.read_excel(r'D:\superstore_2011-2015.xlsx')
df.head(3)

2.获取需要分析字段

df = df[['顾客编号','顾客类型','总额']]
df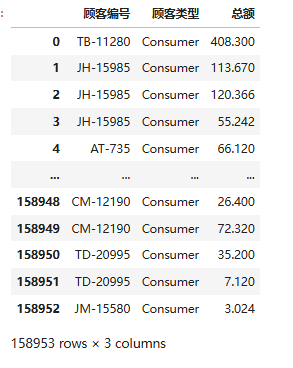

3. 分组时可用min函数保留相同字符串的字段

df.groupby('顾客编号').aggregate({'顾客类型':min,'总额':sum}) 
#分组时可用min函数保留相同字符串的字段

1.2.2 图形可视化

1.箱型图

df_buyer = df.groupby('顾客编号').aggregate({'顾客类型':min,'总额':sum}) 
sns.boxplot(data=df_buyer,y='总额')

2.分类型箱型图

plt.rcParams['axes.unicode_minus'] = False
sns.set_style('whitegrid',{'font.sans-serif':['SimHei','Arial']})
df_buyer = df.groupby('顾客编号').aggregate({'顾客类型':min,'总额':sum}) 
sns.boxplot(data=df_buyer,x='顾客类型',y='总额')

3.增强型箱型图

plt.rcParams['axes.unicode_minus'] = False
sns.set_style('whitegrid',{'font.sans-serif':['SimHei','Arial']})
df_buyer = df.groupby('顾客编号').aggregate({'顾客类型':min,'总额':sum}) 
sns.boxenplot(data=df_buyer,x='顾客类型',y='总额')

4.seaborn.histplot()直方图绘制

sns.histplot(data=df_buyer,x='总额',stat='probability',binwidth=500,hue='顾客类型')

1.横轴为总额（横轴必须是连续字段）

2.每一个区间的数据的数量（100个...）作为直方图的高度，

3.每个柱形或者每一个区间它的宽度

参数：用变量x可以指定横轴

stat 也就是统计的缩写

stat='probability' 表示这个数出现的频率，也就是比例

binwidth=500 每个区间的跨度都是500元，如：0-500元，500-1000元

hue='顾客类型' 用不同的颜色区分不同的顾客类型

bins=[0,1000,10000,20000,30000] 人为划分区间

kde=True 将柱形高低绘制成平滑曲线¶

sns.histplot(data=df_buyer,x='总额',kde=True)

人为划分区间bins

sns.histplot(data=df_buyer,x='总额',bins=[0,1000,10000,20000,30000])

使用 Seaborn 的 displot 函数创建一个分面图（Facet Grid），用于展示不同顾客类型下的 “总额” 分布情况。

sns.displot(
    data=df_buyer,       # 数据源（Pandas DataFrame）
    x='总额',            # X轴：数值型变量（如消费总额）
    col='顾客类型',      # 按列分面：将不同顾客类型的分布绘制成独立子图
)

1.2.3 cut函数划分数据区间

Pandas.cut（）按照指定分割点，计算每个数据分别处于哪一个区间

pd.cut() 关键参数

参数	作用	示例
`bins`	分箱边界： - 列表：自定义区间（如 `[0, 1000, 10000]`） - 整数：自动划分 N 个等宽区间（如 `bins=5`）	`bins=[0, 500, 1000, float('inf')]`
`labels`	自定义每个区间的标签（需与 `bins` 长度匹配）	`labels=['低', '中', '高']`
`right`	是否包含右边界（默认 `True`，即左开右闭区间 `(a, b]`）	`right=False` → 左闭右开 `[a, b)`
`include_lowest`	是否包含最小值（处理边界值）	`include_lowest=True`

pd.cut(df_buyer['总额'],bins=[0,1000,10000,20000,30000])

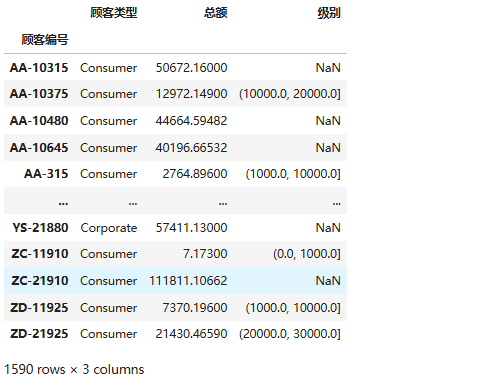
使用 pandas.cut() 函数将 df_buyer 中的 总额 列进行分箱（Binning）操作，根据消费金额将客户划分为不同级别，并将结果存储在新列 级别 中。

df_buyer['级别'] = pd.cut(
    df_buyer['总额'],                  # 待分箱的列
    bins=[0, 1000, 10000, 20000, 30000]  # 分箱边界（左开右闭区间）
)

分箱规则：

区间范围	对应级别（自动生成）
0 ≤ 总额 < 1000	`(0, 1000]`
1000 ≤ 总额 < 10000	`(1000, 10000]`
10000 ≤ 总额 < 20000	`(10000, 20000]`
20000 ≤ 总额 < 30000	`(20000, 30000]`

分析不同级别客户特征

df_buyer['级别']=pd.cut(df_buyer['总额'], bins=[0, 1000, 10000, 20000, 30000],labels=['穷','中','富','壕'])
df_buyer

统计各级别客户数量

level_counts = df_buyer['级别'].value_counts().sort_index()
print(level_counts)

与其他变量关联分析

# 分析级别与性别、年龄等的关系
sns.barplot(data=df_buyer, x='级别', y='年龄', hue='性别')

注意事项

区间开闭问题：

默认 right=True，即 (a, b]，若需左闭右开（如 [a, b)），需设置 right=False。

缺失值处理：
pd.cut() 会将 NaN 保留为 NaN，若需特殊处理，可先填充：
df_buyer['总额'] = df_buyer['总额'].fillna(0)  # 将NaN填充为0
边界值处理：

若数据中存在刚好等于边界的值，需通过 include_lowest=True 确保最小值被包含。

1.2.4 绘制自定义分区的直方图

df_level = df_buyer.groupby('级别').count()
df_level

sns.barplot(data=df_level,x=df_level.index,y='总额')

2. 核密度估计法

** 核密度估计法（Kernel Density Estimation，KDE）** 是一种非参数统计方法，用于估计随机变量的概率密度函数（PDF）。它通过核函数对数据点进行平滑拟合，从而揭示数据的分布形态（如单峰、多峰、对称性等），无需预先假设数据服从特定分布（如正态分布）。

2.1 基本原理

对于每个数据点 xi，用一个核函数（如正态分布曲线）在其周围 “扩散” 一个概率密度值，然后将所有数据点的核函数结果叠加，得到整体的密度估计曲线。
公式表示为：

其中：

n 是数据点数量，

h 是带宽（Bandwidth）（控制平滑程度的参数），

K(⋅) 是核函数（常用核函数包括正态核、均匀核、三角核等）。

关键参数

带宽（h）：

h 越小，曲线越 “尖锐”，保留更多局部细节，但可能过拟合（噪声明显）；

h 越大，曲线越平滑，可能掩盖真实分布特征（如多峰结构）。

核函数类型：
常用核函数对结果影响较小，默认选择正态核（最平滑）。

核函数类型：
常用核函数对结果影响较小，默认选择正态核（最平滑）。

2.2 核密度估计 vs. 直方图

对比维度	直方图	核密度估计
数据展示形式	离散化区间（分箱）的频数 / 频率	连续平滑的密度曲线
依赖参数	分箱数、箱宽	带宽 h、核函数类型
优势	直观展示数据分布的大致轮廓	揭示分布的细微特征（如多峰）
缺点	分箱方式影响结果，可能丢失细节	结果抽象，需结合实际数据理解

2.3常用场景

探索数据分布

识别数据是否为单峰、多峰分布，是否存在离群值或异常区域。

示例：分析用户消费金额的分布是否呈现 “长尾效应” 或 “双峰特征”。

对比组间分布差异

对不同分组数据（如不同性别、不同地区）分别绘制核密度曲线，观察分布的位置、形状差异。

示例：比较新老用户的消费金额分布是否存在显著偏移。

与其他图表结合

脊线图（Ridgeline Plot）：展示多个分组的核密度曲线沿某一维度排列，适合对比分布的变化趋势。

等高线图 / 二维核密度图：用于二维数据（如 x 和 y 变量），展示数据在平面上的密度分布（类似地形图）。

<