Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional (傅立叶特征使网络在低维域学习高频函数)

顾默@

已于 2024-04-13 00:33:34 修改

阅读量970

点赞数 2

分类专栏：有关论文的一些算法文章标签：学习 pytorch 图像处理 python linux

于 2024-04-10 21:33:27 首次发布

本文链接：https://blog.csdn.net/weixin_53765004/article/details/137611475

版权

Abstract

我们展示了通过一个简单的傅里叶特征映射传递输入点可以使多层感知机(MLP)学习低维问题域中的高频函数。这些结果揭示了计算机视觉和图形的最新进展，通过使用 MLP 来表示复杂的3D 对象和场景，实现了最先进的结果。使用来自神经切线核(NTK)文献的工具，我们表明，标准的 MLP 无论在理论上还是在实践中都无法学习高频。为了克服这种光谱偏差，我们使用傅里叶特征映射将有效的 the neural tangent kernel (NTK) 转换成带宽可调的平稳核。我们提出了一种选择特定问题的傅里叶特征的方法，这种方法可以大大提高与计算机视觉和图形社区相关的低维回归任务的 MLP 的性能。

Introduction

最近在计算机视觉和图形方面的一系列研究用深度完全连接网络(也称为多层感知器或 MLP)参数化的连续函数取代了对象、场景几何和外观的传统离散表示方法(例meshes and voxel grids网格和体素网格) ·。这些 MLP，我们称之为基于坐标的”MLP，以低维坐标作为输入(通常在三维中的点) ，并被训练以在每个输入位置输出形状，密度和/或颜色的表示(参见图1)。
在这里插入图片描述
图1:傅里叶特征改善了各种高频低维回归任务的基于坐标的 MLP 的结果，包括直接(b，c)和间接(d，e)监督。我们可视化一个图像回归任务(b)的示例 MLP (a) ，其中网络的输入是一个像素坐标，输出是该像素的颜色。将坐标直接传递到网络(顶部)会产生模糊的图像，而使用傅里叶特征映射(底部)对输入进行预处理使 MLP 能够表示更高频率的细节。

这个策略很有说服力，因为基于坐标的 MLP 可以适应基于梯度的优化和机器学习，而且可以比网格采样的表示数量级更紧凑。已经使用基于坐标的 MLP 来表示图像(称为“组合模式生成网络”) ，体积密度，占用率和符号距离，并且已经在形状表示，纹理合成，来自图像的形状推断和新视图合成等多种任务中取得了最先进的结果。

我们利用最近在使用神经切线核(NTK)的核回归建模深度网络行为方面的进展，从理论和实验上表明标准 MLP 不适合这些低维坐标视觉和图形任务。特别是，MLP 难以学习高频函数，这种现象在文献中被称为“光谱偏差”。NTK 理论认为，这是因为标准的基于坐标的 MLP 对应的核具有快速的频率下降，这有效地阻止了它们能够表示自然图像和场景中存在的高频内容。

最近的一些工作已经实验性地发现，输入坐标的启发式正弦映射(称为“位置编码”)允许 MLP 表示更高的频率内容。我们观察到这是傅里叶特征的一个特例 : 将输入坐标 v 映射到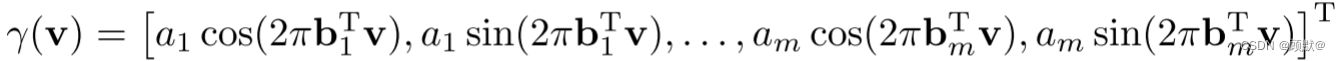在这里插入图片描述
然后将它们传递给 MLP。我们表明，这种映射将 NTK 转换成一个平稳(平移不变)的内核，并能够通过修改频率向量 bj 来调整 NTK 的频谱，从而控制相应的 MLP 可以学习的频率范围。我们表明，设置 aj = 1和从各向同性分布中随机抽样 bj 的简单策略取得了良好的性能，并且这个分布的规模(标准差)远远大于它的具体形状。我们用这种傅里叶特征输入映射训练 MLP 跨越一系列与计算机视觉和图形社区相关的任务。如图1所示，我们提出的映射显著提高了基于坐标的 MLP 的性能。总之，我们作出以下贡献:
1.我们利用 NTK 理论和简单的实验表明，傅里叶特征映射可以用来克服基于坐标的 MLP 对低频的光谱偏差，通过允许他们学习更高的频率(第4节)。
2.我们证明了一个适当选择尺度的随机傅里叶特征映射可以显著改善计算机视觉和图形学中许多低维任务中基于坐标的 MLP 的性能(第5节)。

related work

我们的工作受到广泛使用基于坐标的 MLP 来表示各种视觉信号(包括图像和3D 场景)的激励。特别是，我们的分析旨在澄清实验结果，表明使用对数间隔轴对齐频率的正弦曲线的坐标输入映射(他们称之为“位置编码”)改善了基于坐标的 MLPs 在二维图像的新视图合成任务上的性能和来自冷冻电子显微的蛋白质结构建模。我们分析了这种技术，表明它对应于 MLP 的 NTK 的修改，并且我们表明，其他非轴对齐的频率分布可以优于这种位置编码。

先前在自然语言处理和时间序列分析方面的著作使用了类似的位置编码来表示时间或一维位置。特别是，Xu 等人利用随机傅里叶特征(RFF)逼近具有正弦输入映射的平稳核，并提出技术来调整映射参数。我们的工作通过直接解释这种映射为结果网络的 NTK 的修改来扩展它。此外，我们还解决了多维坐标的嵌入，这是视觉和图形任务所必需的。

为了分析在通过 MLP 之前将傅立叶特征映射应用于输入坐标的影响，我们依赖于最近的理论工作：使用 NTK 在无限宽度和无限小学习率的限制下建模神经网络作为核回归。特别是，我们使用了 Lee 等人和 Arora 等人的分析，这些分析整个梯度下降法网络的输出仍然接近那些收敛速度受 NTK 矩阵特征值支配的线性动态系统。对 NTK 特征分解的分析表明，其特征值谱作为频率的函数迅速衰减，这解释了广泛观察到的深度网络对学习低频函数的“光谱偏差”。

我们利用这个分析来考虑在网络之前添加一个傅里叶特征映射的含义/问题，并且我们表明这个映射对 NTK 的特征值谱和相应的网络的收敛性质在实际中有显著的影响。