[文献阅读] (VaDE)Variational Deep Embedding: An Unsupervised and Generative Approach to Clustering

本文链接：https://blog.csdn.net/weixin_53834244/article/details/145797713

文献信息：腾讯2017年发在IJCAI上的一篇论文[1611.05148] Variational Deep Embedding: An Unsupervised and Generative Approach to Clustering，提出了使用VAE和GMM的一种新的聚类模型VaDE

摘要

得益于VAE（变分自编码器）的研究，这一成果很快被用于聚类任务的研究上，人们希望在聚类上这会比传统的自编码器效果更好。

在该论文中，提出了一个聚类框架，VaDE(Variational Deep Embedding)，它结合了VAE和用于聚类任务的高斯混合模型GMM。与传统的VAE不同，关键的区别在于，VaDE使用混合的高斯先验来代替VAE的单一高斯先验，这种先验本质上适用于聚类任务。

实验结果表明，VaDE在不同模式的5个基准上显著优于最先进的聚类方法。

Abstract

This week’s report examines VaDE (Variational Deep Embedding), which combines Variational Autoencoders (VAEs) and Gaussian Mixture Models (GMMs) for unsupervised clustering. Unlike traditional VAEs that use a single Gaussian prior, VaDE employs a mixture of Gaussians to better capture the distribution of data for clustering. The model integrates a deep neural network with a GMM to generate data and uses the evidence lower bound (ELBO) for optimization. Experimental results demonstrate VaDE’s superior performance over state-of-the-art clustering methods on multiple benchmarks. The report also includes a PyTorch implementation and analysis of VaDE’s effectiveness in clustering tasks, highlighting its potential for unsupervised learning applications.

GMM(高斯混合模型)

混合模型

混合模型是一个可以用来表示在总体分布（distribution）中含有 K 个子分布的概率模型，换句话说，混合模型表示了观测数据在总体中的概率分布，它是一个由 K 个子分布组成的混合分布。混合模型不要求观测数据提供关于子分布的信息，来计算观测数据在总体分布中的概率。

高斯混合模型

高斯混合模型可以看作是由 K 个单高斯模型组合而成的模型，这 K 个子模型是混合模型的隐变量（Hidden variable）。一般来说，一个混合模型可以使用任何概率分布，这里使用高斯混合模型是因为高斯分布具备很好的数学性质以及良好的计算性能。

举个不是特别稳妥的例子，比如我们现在有一组狗的样本数据，不同种类的狗，体型、颜色、长相各不相同，但都属于狗这个种类，此时单高斯模型可能不能很好的来描述这个分布，因为样本数据分布并不是一个单一的椭圆，所以用混合高斯分布可以更好的描述这个问题，如下图所示：

图中每个点都由 K 个子模型中的某一个生成。

在聚类任务上，GMM算法认为，每一个聚类都可以用一个高斯分布来描述，而数据集则可以被认为是这些高斯分布的混合。GMM的目标是：找出最能代表数据的高斯分布的参数（均值、协方差和混合系数）。

EM（期望最大化）算法通常用于优化GMM的参数。(EM算法)迭代地执行以下两个步骤：

期望步骤 (E-step)：给定当前的模型参数，计算数据点属于每个聚类的概率。
最大化步骤 (M-step)：更新模型参数以最大化观测数据的似然。

关于GMM具体原理见高斯混合模型（GMM），比较详细易懂

这里只贴一下教科书的定义，方便回顾

VaDE

生成过程

文章首先描述生成过程，这是为了对先验过程下一个定义。

VaDE通过一个高斯混合模型（Gaussian Mixture Model, GMM）和一个深度神经网络（a deep neural network, DNN）来建模数据生成的过程。建模的过程分为3步：

由GMM选择一个cluster（c）；
根据cluster生成一个潜在的embedding（z）；
用DNN将embedding解码码为observable（x’）。VaDE的优化还是以VAE的形式，所以加了一个不同的DNN来将observable编码码为潜在embedding，这样证据下限（evidence lower bound, ELBO）就能用随机梯度变分贝叶斯（Stochastic Gradient Variational Bayes, SGVB）和重参数技巧（reparameterization trick）进行优化了。

下图是VaDE的结构图。

在这里插入图片描述

生成过程的数学描述

在这里插入图片描述

其中，K是预定义好的值，这里我们知道K=10， $π_k$ 是聚类器 k 的先验分布，则 $π∈R_+^K$ ,那么属于每一类的概率和即为1（ $_{k=1}^{10}π_k=1$ ）， $C a t (π)$ 是类别分布。选择好cluster c 后，则可以得到对应的高斯混合模型的均值 $μ_c$ 和方差 $σ_c^2$ ，从而采样到潜在变量 z 。用DNN f(z;θ) 将z编码为观测样本 x 了。联合概率 $p (x, z, c)$ 可以分解为： $p (x, z, c) = p (x ∣ z) p (z ∣ c) p (c)$ 。因为他们是条件独立的，所以概率又可以定义为

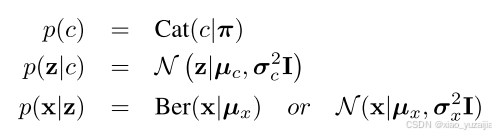
在这里插入图片描述

定义这些先验概率用于推导目标函数。

变分下界（证据下界ELBO）

我们要找到目标 $l o g (P (x))$ 的一个下界，这个下界称为证据下界ELBO。通过最大化证据下界ELBO，从而最大化给定数据的似然 $l o g (P (x))$ 。

关于证据下界ELBO的推导方式，原文使用的是Jensen’s不等式得到的。还有一种方式就是[1606.05908] Tutorial on Variational Autoencoders中使用的，会易懂一些，可见上一篇博客https://blog.csdn.net/weixin_53834244/article/details/145667771?spm=1001.2014.3001.5501

与VAE相比，VaDE在公式推导中多了一个变量c。

通过Jensen’s不等式，log似然可以写作

在这里插入图片描述

如果使用Tutorial on Variational Autoencoders的推导结果的话，也可以直接写成这个形式

在这里插入图片描述

其中， $L_{ELBO}$ 是evidence lower bound， q(z,c|x) 是变分后验，用于逼近真实后验 p(z,c|x) ，其可以被分解为：

在这里插入图片描述

于是 $L_{ELBO}$ 可以写成

在这里插入图片描述

最后使用SGVB估计器和重参数化技巧，LELBO(x)可以重写为如下。这五项的展开比较复杂，具体推导可以看变分深度嵌入(Variational Deep Embedding, VaDE) - 凯鲁嘎吉 - 博客园

在这里插入图片描述

梳理一下算法流程

结果

在这里插入图片描述

在MNIST上作者特意与VAE+GMM做了比较，这个VAE+GMM在观测空间上使用VAE，然后直接在VAE潜空间上使用GMM。而VaDE与此的不同在于，第二项KL项中，混合高斯先验 $p (z, c)$ 代替了传统VAE的 $N (0, I)$ 先验。并且让GMM的三个参数 $\mu,σ)$ 都参与梯度下降。

在这里插入图片描述

所以作者专门做了此对比，来说明第二项KL项的重要性。

在这里插入图片描述

实验

https://github.com/GuHongyang/VaDE-pytorch

import torch
import torch.nn as nn
import torch.nn.functional as F
from tqdm import tqdm
from torch.optim import Adam
import itertools
from sklearn.mixture import GaussianMixture
from sklearn.metrics import accuracy_score
import numpy as np
import os

import ipdb


def cluster_acc(Y_pred, Y):
    from sklearn.utils.linear_assignment_ import linear_assignment
    assert Y_pred.size == Y.size
    D = max(Y_pred.max(), Y.max())+1
    w = np.zeros((D,D), dtype=np.int64)
    for i in range(Y_pred.size):
        w[Y_pred[i], Y[i]] += 1
    ind = linear_assignment(w.max() - w)
    return sum([w[i,j] for i,j in ind])*1.0/Y_pred.size, w


def block(in_c,out_c):
    layers=[
        nn.Linear(in_c,out_c),
        nn.ReLU(True)
    ]
    return layers

class Encoder(nn.Module):
    def __init__(self,input_dim=784,inter_dims=[500,500,2000],hid_dim=10):
        super(Encoder,self).__init__()

        self.encoder=nn.Sequential(
            *block(input_dim,inter_dims[0]),
            *block(inter_dims[0],inter_dims[1]),
            *block(inter_dims[1],inter_dims[2]),
        )

        self.mu_l=nn.Linear(inter_dims[-1],hid_dim)
        self.log_sigma2_l=nn.Linear(inter_dims[-1],hid_dim)

    def forward(self, x):
        e=self.encoder(x)

        mu=self.mu_l(e)
        log_sigma2=self.log_sigma2_l(e)

        return mu,log_sigma2


class Decoder(nn.Module):
    def __init__(self,input_dim=784,inter_dims=[500,500,2000],hid_dim=10):
        super(Decoder,self).__init__()

        self.decoder=nn.Sequential(
            *block(hid_dim,inter_dims[-1]),
            *block(inter_dims[-1],inter_dims[-2]),
            *block(inter_dims[-2],inter_dims[-3]),
            nn.Linear(inter_dims[-3],input_dim),
            nn.Sigmoid()
        )



    def forward(self, z):
        x_pro=self.decoder(z)

        return x_pro


class VaDE(nn.Module):
    def __init__(self,args):
        super(VaDE,self).__init__()
        self.encoder=Encoder()
        self.decoder=Decoder()

        self.pi_=nn.Parameter(torch.FloatTensor(args.nClusters,).fill_(1)/args.nClusters,requires_grad=True)
        self.mu_c=nn.Parameter(torch.FloatTensor(args.nClusters,args.hid_dim).fill_(0),requires_grad=True)
        self.log_sigma2_c=nn.Parameter(torch.FloatTensor(args.nClusters,args.hid_dim).fill_(0),requires_grad=True)


        self.args=args


    def pre_train(self,dataloader,pre_epoch=10):

        if  not os.path.exists('./pretrain_model.pk'):

            Loss=nn.MSELoss()
            opti=Adam(itertools.chain(self.encoder.parameters(),self.decoder.parameters()))

            print('Pretraining......')
            epoch_bar=tqdm(range(pre_epoch))
            for _ in epoch_bar:
                L=0
                for x,y in dataloader:
                    if self.args.cuda:
                        x=x.cuda()

                    z,_=self.encoder(x)
                    x_=self.decoder(z)
                    loss=Loss(x,x_)

                    L+=loss.detach().cpu().numpy()

                    opti.zero_grad()
                    loss.backward()
                    opti.step()

                epoch_bar.write('L2={:.4f}'.format(L/len(dataloader)))

            self.encoder.log_sigma2_l.load_state_dict(self.encoder.mu_l.state_dict())

            Z = []
            Y = []
            with torch.no_grad():
                for x, y in dataloader:
                    if self.args.cuda:
                        x = x.cuda()

                    z1, z2 = self.encoder(x)
                    assert F.mse_loss(z1, z2) == 0
                    Z.append(z1)
                    Y.append(y)

            Z = torch.cat(Z, 0).detach().cpu().numpy()
            Y = torch.cat(Y, 0).detach().numpy()

            gmm = GaussianMixture(n_components=self.args.nClusters, covariance_type='diag')

            pre = gmm.fit_predict(Z)
            print('Acc={:.4f}%'.format(cluster_acc(pre, Y)[0] * 100))

            self.pi_.data = torch.from_numpy(gmm.weights_).cuda().float()
            self.mu_c.data = torch.from_numpy(gmm.means_).cuda().float()
            self.log_sigma2_c.data = torch.log(torch.from_numpy(gmm.covariances_).cuda().float())

            torch.save(self.state_dict(), './pretrain_model.pk')

        else:


            self.load_state_dict(torch.load('./pretrain_model.pk'))




    def predict(self,x):
        z_mu, z_sigma2_log = self.encoder(x)
        z = torch.randn_like(z_mu) * torch.exp(z_sigma2_log / 2) + z_mu
        pi = self.pi_
        log_sigma2_c = self.log_sigma2_c
        mu_c = self.mu_c
        yita_c = torch.exp(torch.log(pi.unsqueeze(0))+self.gaussian_pdfs_log(z,mu_c,log_sigma2_c))

        yita=yita_c.detach().cpu().numpy()
        return np.argmax(yita,axis=1)


    def ELBO_Loss(self,x,L=1):
        det=1e-10

        L_rec=0

        z_mu, z_sigma2_log = self.encoder(x)
        for l in range(L):

            z=torch.randn_like(z_mu)*torch.exp(z_sigma2_log/2)+z_mu

            x_pro=self.decoder(z)

            L_rec+=F.binary_cross_entropy(x_pro,x)

        L_rec/=L

        Loss=L_rec*x.size(1)

        pi=self.pi_
        log_sigma2_c=self.log_sigma2_c
        mu_c=self.mu_c

        z = torch.randn_like(z_mu) * torch.exp(z_sigma2_log / 2) + z_mu
        yita_c=torch.exp(torch.log(pi.unsqueeze(0))+self.gaussian_pdfs_log(z,mu_c,log_sigma2_c))+det

        yita_c=yita_c/(yita_c.sum(1).view(-1,1))#batch_size*Clusters

        Loss+=0.5*torch.mean(torch.sum(yita_c*torch.sum(log_sigma2_c.unsqueeze(0)+
                                                torch.exp(z_sigma2_log.unsqueeze(1)-log_sigma2_c.unsqueeze(0))+
                                                (z_mu.unsqueeze(1)-mu_c.unsqueeze(0)).pow(2)/torch.exp(log_sigma2_c.unsqueeze(0)),2),1))

        Loss-=torch.mean(torch.sum(yita_c*torch.log(pi.unsqueeze(0)/(yita_c)),1))+0.5*torch.mean(torch.sum(1+z_sigma2_log,1))


        return Loss






    def gaussian_pdfs_log(self,x,mus,log_sigma2s):
        G=[]
        for c in range(self.args.nClusters):
            G.append(self.gaussian_pdf_log(x,mus[c:c+1,:],log_sigma2s[c:c+1,:]).view(-1,1))
        return torch.cat(G,1)




    @staticmethod
    def gaussian_pdf_log(x,mu,log_sigma2):
        return -0.5*(torch.sum(np.log(np.pi*2)+log_sigma2+(x-mu).pow(2)/torch.exp(log_sigma2),1))