动态规划：完全背包下的组合数与排列数问题

最新推荐文章于 2023-12-10 15:02:23 发布

不是黏人精

最新推荐文章于 2023-12-10 15:02:23 发布

阅读量186

点赞数 2

文章标签：动态规划算法

本文链接：https://blog.csdn.net/weixin_53928977/article/details/129272652

版权

首先，将一切模板忘记，将滚动数组忘记。把目光集中于【动态规划】本身。什么是动态规划的特性？【最优子结构】、【重叠子问题】、【状态转移方程】！

如何判断这个问题和最优子结构是否有关？和重叠子问题是否有关？画出搜索树！准确的来说，【用回溯法手动画出搜索树】！

这是方法论根本！！依据搜索树，不仅可以查看是否存在【重叠子问题】，也可以发掘【状态转移方程】，所谓动态规划/记忆化搜索，只不过是**【优化穷举法的“奇技淫巧”】**

通过题目来入手吧！

完全背包下的组合数：518零钱兑换II

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

题目数据保证结果符合 32 位带符号整数。

先说结论！实际上，这题画出搜索树作用不是很大

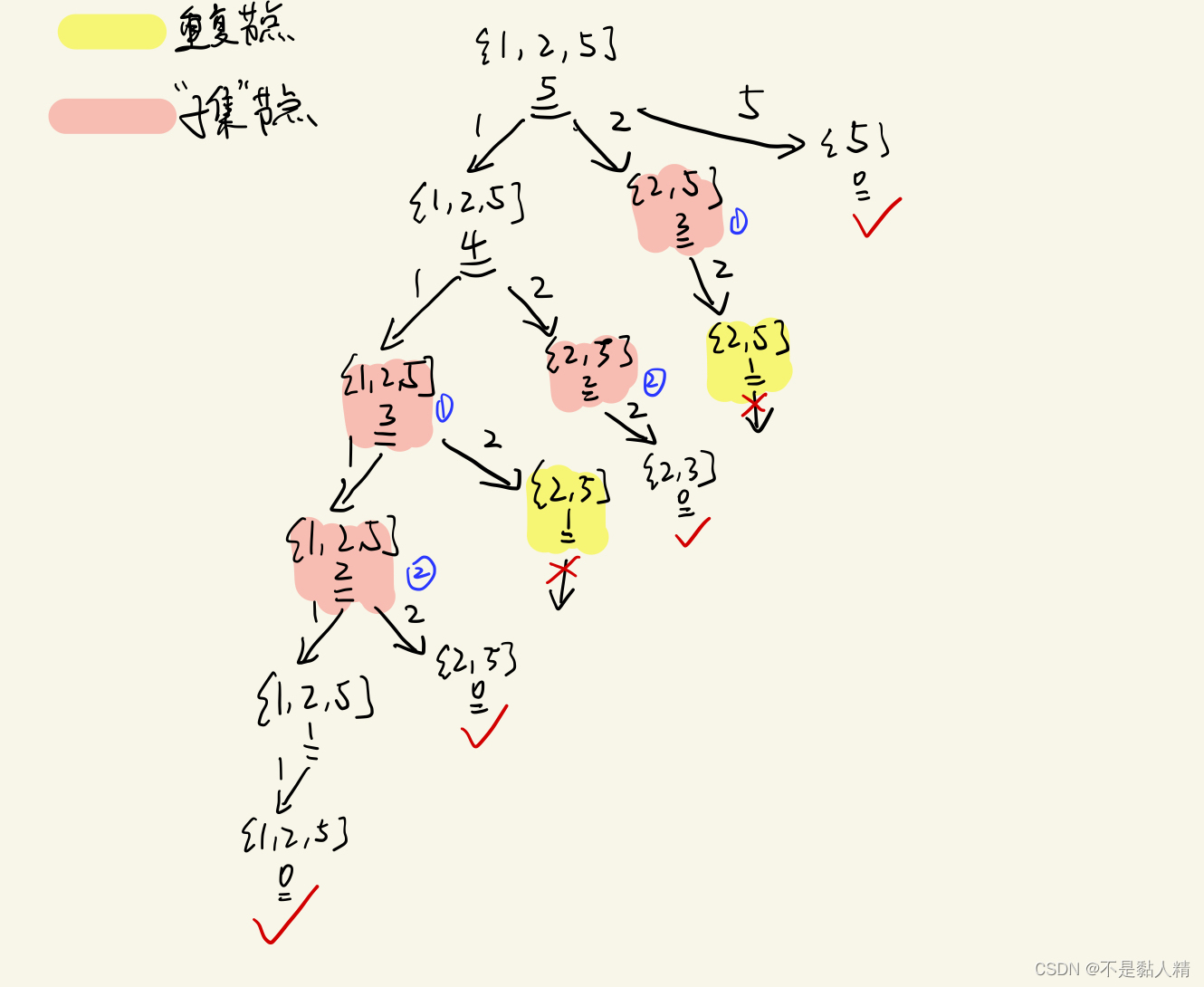
如图所示，图中的【重复节点】很少，由于组合数的性质，为了去重（例如：{2，1，1} 和 {1，2，1}是等价的），那么导致每个节点的状态之一【选择集合】有所不同，因此我们只能通过dp数组的定义来推导它们之间的关系，也就是【状态转移方程】

并且需要强调的是！dp数组一定要定义成二维的，因为我们的状态之一【选择集合】在搜索中不断变化（在不考虑【空间压缩】这一优化手段时 ）。

dp数组的定义：dp[i][j]，使用coins中的 i 个硬币，可以组成金额 j 的方法（组合数）是多少？
状态转移方程如何确定？其实这一步就是利用了【”子集“节点】（这是我自己定义的节点，意思是其中一个节点的所有状态（选择集合，目标值）是另一个节点所有状态的子集）那么如何推导呢？从dp数组的定义入手！首先分情况考虑：

if(j >= coins[i-1]) {
		dp[i][j] = dp[i-1][j] + dp[i][j-coins[i-1]];
}
else {
		dp[i][j] = dp[i-1][j];
}

if … 成立时，说明我们可以从【选择集合】中，挑选当前硬币，来凑目标值。由于我们考虑的问题是【凑成目标值的组合数】，那么我们当然可以不挑选当前硬币，也可以挑选当前硬币。前者对应的就是 dp[i-1][j]，后者对应的就是dp[i][j-coins[i-1]

为什么在第二个维度一定是 j-coins[i-1] 呢？为了保证真的做了挑选！构成 dp[i][j-coins[i-1] 时，由于第一维度是 i 而不是 i-1，因此在凑成 目标值 = j-coins[i-1] 时，可以挑选 coins[i-1] ，也可以不挑选 coins[i-1] （ j-coins[i-1] >= j 的情况下）(本质和我们现在计算dp[i][j]的逻辑是一致的)，为了避免重复计算不挑选coins[i-1] 的情况，所以 **第二维度一定是 j-coins[i-1] 保证我们真的挑选了【coins[i-1]】

至此可以发现，画出回溯法搜索树，确实帮助不大！但是在排列数是大大不同

考虑压缩空间的完全背包组合数问题

压缩空间这回事，只和【base case】和【状态转移方程】挂钩，在二维dp数组下，【base case】也就是：dp[i][0] = 1 而【状态转移方程】是 dp[i][j] = dp[i-1][j] + dp[i][j-coins[i-1]]; 或 dp[i][j] = dp[i-1][j];

考虑压缩第一个维度 i ，如图所示。

我们考虑一下：

base case怎么处理？

由于dp[i][0] = 1，去除维度i后，直接将dp[0]初始化为1即可

去除维度i后，在更新dp[j]之前：

dp[j]对应什么？——dp[i-1][j]
dp[j-coins[i-1]]对应什么？——dp[i][j-coins[i-1]]

那么很容易写出：

vector<int> dp(amount+1, 0);
dp[0] = 1;
for(int i = 1; i <= n; ++i) {
    for(int j = 1; j <= amount; ++j) {
        if(j >= coins[i-1]) {
            dp[j] = dp[j] + dp[j-coins[i-1]];
        }
        else {
            dp[j] = dp[j];
        }
    }
}
return dp[amount];

完全背包下的排列数：377. 组合总和 Ⅳ

给你一个由不同整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。

题目数据保证答案符合 32 位整数范围。

此题画出搜索树大有可为！与组合数不同，排列数讲究顺序，因此在【选择集合】做出选择后，【选择集合】这一状态不变！

如图所示：

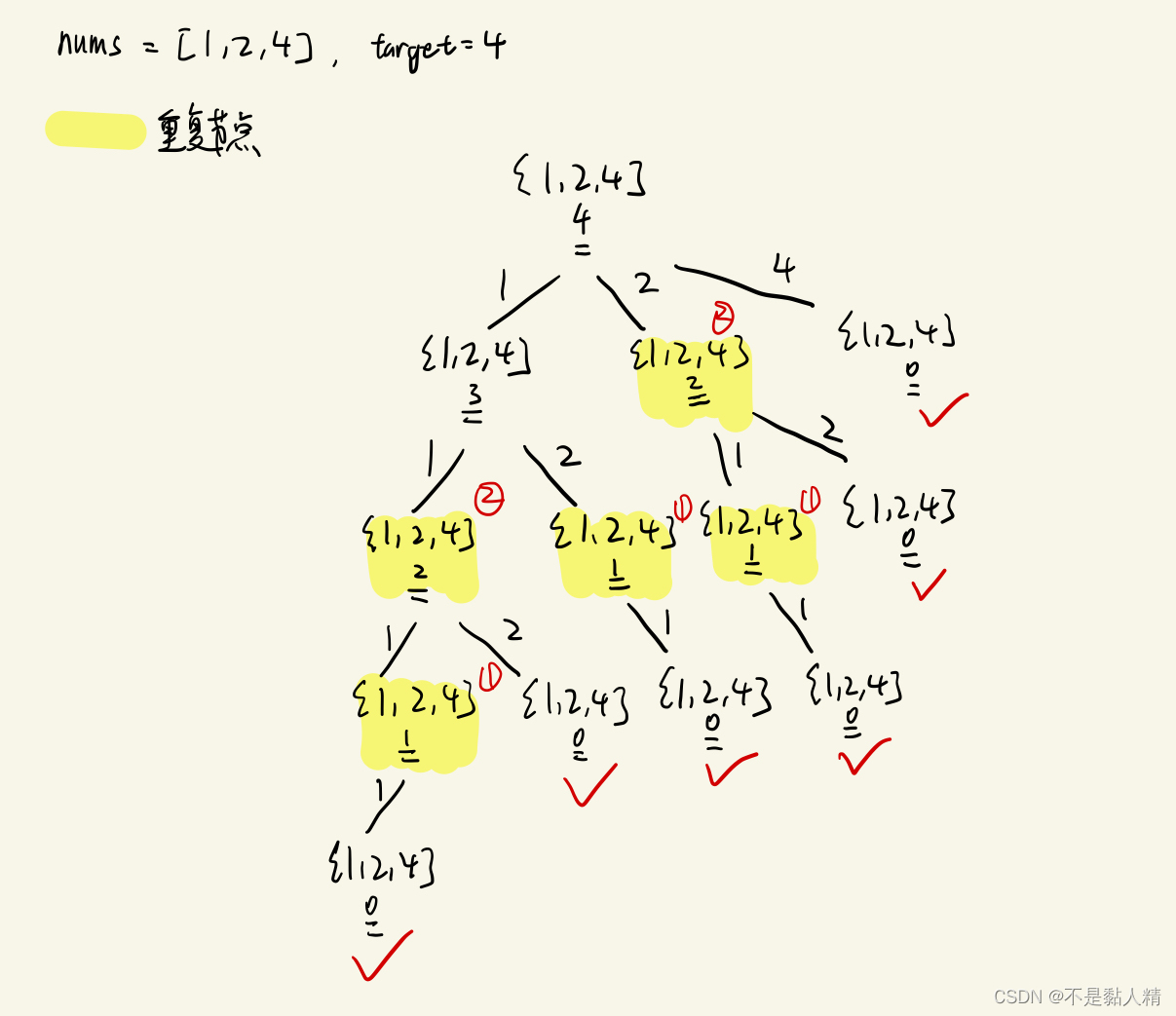
画出搜索树后可以发现，其实所谓的【状态】，只有一个！那就是【目标值】，至于【选择集合】，它在每个节点中都一样，是不变化的，所以它不是状态！

它仅仅是选择！是【导致状态变化的行为】

由图中的【 {1，2，4} | 2 】可以看出，计算它的值，也就是计算它做每个选择时对应的值的和，也就是说它存在重叠子问题！

我们很自然可以写出dp数组的定义，dp[j] 意味着任意挑选nums的目标值为 j 的排列数有几种？

很自然写出：

vector<int> dp(target+1, 0);
// base case
dp[0] = 1;
for(int j = 1; j <= target; ++j) {
		// long int 是为了防止溢出
		// j_sum 记录目标值为j时，通过各个选择得到的排列数
    long int j_sum = 0;
    for(int i = 0; i < n; ++i) {
        if(j >= nums[i]) {
            j_sum += dp[j-nums[i]];
        }
				// 完整展示逻辑
				else {
						j_sum += 0;
				}
    }
    dp[j] = j_sum;
}
return dp[target];

至此，我们通过搜索树可以发现，完全背包下的排列数，其实只有一种状态；而完全背包下的组合数，是有两个状态的！它们是【选择集合】与【目标值】，在做不同选择时（选择nums[i-1]与否）可能会导致【选择集合的变化】，也会导致【目标值】的变化