力扣每日一题：790. 多米诺和托米诺平铺 【dp动态规划】

有两种形状的瓷砖：一种是 2 x 1 的多米诺形，另一种是形如 "L" 的托米诺形。两种形状都可以旋转。

给定整数 n ，返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模 的值。

平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。

示例 1:

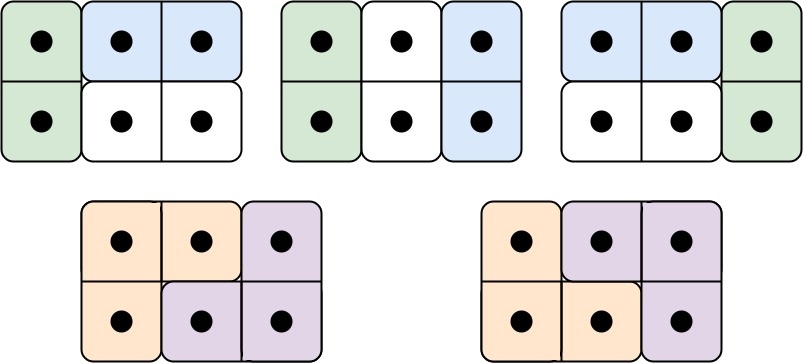
输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。

示例 2:

输入: n = 1
输出: 1

提示：

• 1 <= n <= 1000

分析：“平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。”，整句话整的不是很明白，但是这次的官方题解确实是给力，推荐大家直接看官方题解。然后在说说自己对这道题的理解。这个下一个怎么摆放是和上一个状态有关系的，那么上一次的摆放可以分为几个状态呢，大家可以分析一下，首先我们知道这是一宽为2的长方形，然后我们摆放的物品也是宽度为2，这个旧就已经全部填满了，我们只需要判断列的情况。这里就直接引用官方的一个分析

 

考虑这么一种平铺的方式：在第 iii 列前面的正方形都被瓷砖覆盖，在第 iii 列后面的正方形都没有被瓷砖覆盖（iii 从 111 开始计数）。那么第 ii列的正方形有四种被覆盖的情况：

一个正方形都没有被覆盖，记为状态 0；

只有上方的正方形被覆盖，记为状态 1；

只有下方的正方形被覆盖，记为状态 2；

上下两个正方形都被覆盖，记为状态 3。

使用 dp[i][s]\textit{dp}[i][s]dp[i][s] 表示平铺到第 iii 列时，各个状态 sss 对应的平铺方法数量。考虑第 i−1i-1i−1 列和第 iii 列正方形，它们之间的状态转移如下图（红色条表示新铺的瓷砖）：

 

初始时 dp[0][0]=0,dp[0][1]=0,dp[0][2]=0,dp[0][3]=1\textit{dp}[0][0] = 0, \textit{dp}[0][1] = 0, \textit{dp}[0][2] = 0, \textit{dp}[0][3] = 1dp[0][0]=0,dp[0][1]=0,dp[0][2]=0,dp[0][3]=1，对应的状态转移方程（i>0i \gt 0i>0）为：

dp[i][0]=dp[i−1][3]dp[i][1]=dp[i−1][0]+dp[i−1][2]dp[i][2]=dp[i−1][0]+dp[i−1][1]dp[i][3]=dp[i−1][0]+dp[i−1][1]+dp[i−1][2]+dp[i−1][3] \begin{aligned} \textit{dp}[i][0] &= \textit{dp}[i-1][3] \\ \textit{dp}[i][1] &= \textit{dp}[i-1][0] + \textit{dp}[i-1][2] \\ \textit{dp}[i][2] &= \textit{dp}[i-1][0] + \textit{dp}[i-1][1] \\ \textit{dp}[i][3] &= \textit{dp}[i-1][0] + \textit{dp}[i-1][1] + \textit{dp}[i-1][2] + \textit{dp}[i-1][3] \\ \end{aligned}
dp[i][0]
dp[i][1]
dp[i][2]
dp[i][3]
​
  
=dp[i−1][3]
=dp[i−1][0]+dp[i−1][2]
=dp[i−1][0]+dp[i−1][1]
=dp[i−1][0]+dp[i−1][1]+dp[i−1][2]+dp[i−1][3]
​
 
最后平铺到第 nnn 列时，上下两个正方形都被覆盖的状态 dp[n][3]\textit{dp}[n][3]dp[n][3] 对应的平铺方法数量就是总平铺方法数量。

AC代码：

class Solution {
    public int numTilings(int n) {
        int Mod = 1000000007;
        int res =0  ;
        int dp[][] = new int[n+1][4];
        dp[0][3] =1  ;
        for (int i = 1 ; i<=n ;i++){
            dp[i][0]= dp[i-1][3] % Mod ;
            dp[i][1] = (dp[i-1][0]%Mod+dp[i-1][2]%Mod)%Mod ;
            dp[i][2] =(dp[i-1][0]%Mod+dp[i-1][1]%Mod)%Mod ;
// 注意这里取余不要搞错了
            dp[i][3] = (((dp[i-1][0]+dp[i-1][1])%Mod + dp[i-1][2])%Mod +dp[i-1][3])%Mod ;
        }

          


        return dp[n][3] ; 

    }
}