优化器optimizer及实例化代码

原创于 2025-03-07 21:38:38 发布 · 742 阅读

30 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能

人工智能同时被 2 个专栏收录

27 篇文章

订阅专栏

python

9 篇文章

订阅专栏

什么是优化器？

在深度学习中，优化器（Optimizer）是一个核心概念，它负责调整神经网络的权重和偏置，以便最小化损失函数，从而提高模型的准确性和性能。

常见的优化器，包括梯度下降系列（批量梯度下降BGD、随机梯度下降SGD、小批量梯度下降MBGD）、动量法、NAG、Adagrad、RMSprop以及Adam等，它们的核心目标是通过调整学习率、利用梯度信息等手段，高效地最小化损失函数，从而优化和提升神经网络模型的性能。

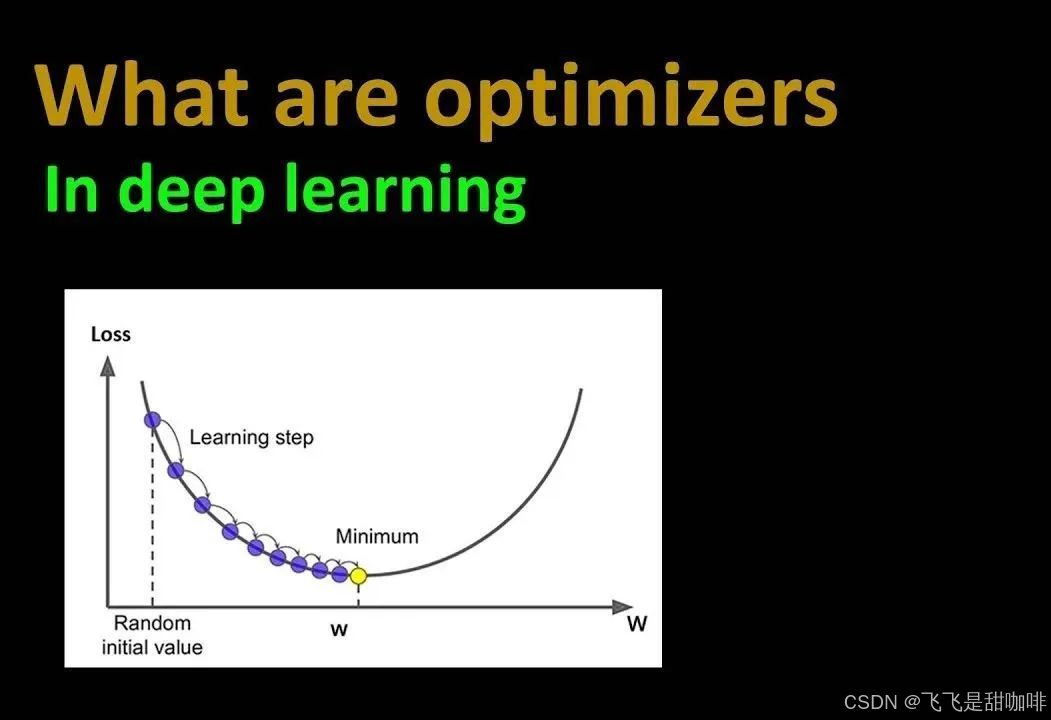
为什么需要优化器？

由于目标函数拥有众多参数且结构复杂，直接寻找最优参数变得十分困难。因此，我们需要借助优化器，它能够逐步调整参数，确保每次优化都朝着最快降低损失的方向前进。

优化器调参

即根据模型实际情况，调整学习率、动量因子、权重衰减等超参数，以优化训练效果和性能。需通过经验和实验找最佳组合，实现快速收敛、减少摆动、防止过拟合。

学习率：过大的学习率可能导致模型无法收敛，而过小的学习率则会使训练过程变得缓慢。因此，需要根据实际情况选择合适的学习率。
动量因子：对于使用动量的优化器，动量因子的选择也很重要。动量因子决定了过去梯度对当前梯度的影响程度。合适的动量因子可以加速收敛，减少摆动。
权重衰减：权重衰减是一种正则化方法，用于防止模型过拟合。在优化器中，可以通过添加权重衰减项来减少模型的复杂度。

优化器使用

每个优化器都是一个类，一定要进行实例化才能使用，比如以下这段代码描述了随机梯度下降（SGD）优化器（带有动量）的一个 Python 类。

class SGD(optimizer_v2.OptimizerV2):

  _HAS_AGGREGATE_GRAD = True

  def __init__(self,
               learning_rate=0.01,
               momentum=0.0,
               nesterov=False,
               name="SGD",
               **kwargs):
    super(SGD, self).__init__(name, **kwargs)
    self._set_hyper("learning_rate", kwargs.get("lr", learning_rate))
    self._set_hyper("decay", self._initial_decay)

    self._momentum = False
    if isinstance(momentum, ops.Tensor) or callable(momentum) or momentum > 0:
      self._momentum = True
    if isinstance(momentum, (int, float)) and (momentum < 0 or momentum > 1):
      raise ValueError("`momentum` must be between [0, 1].")
    self._set_hyper("momentum", momentum)

    self.nesterov = nesterov

  def _create_slots(self, var_list):
    if self._momentum:
      for var in var_list:
        self.add_slot(var, "momentum")

  def _prepare_local(self, var_device, var_dtype, apply_state):
    super(SGD, self)._prepare_local(var_device, var_dtype, apply_state)
    apply_state[(var_device, var_dtype)]["momentum"] = array_ops.identity(
        self._get_hyper("momentum", var_dtype))

  def _resource_apply_dense(self, grad, var, apply_state=None):
    var_device, var_dtype = var.device, var.dtype.base_dtype
    coefficients = ((apply_state or {}).get((var_device, var_dtype))
                    or self._fallback_apply_state(var_device, var_dtype))

    if self._momentum:
      momentum_var = self.get_slot(var, "momentum")
      return gen_training_ops.ResourceApplyKerasMomentum(
          var=var.handle,
          accum=momentum_var.handle,
          lr=coefficients["lr_t"],
          grad=grad,
          momentum=coefficients["momentum"],
          use_locking=self._use_locking,
          use_nesterov=self.nesterov)
    else:
      return gen_training_ops.ResourceApplyGradientDescent(
          var=var.handle,
          alpha=coefficients["lr_t"],
          delta=grad,
          use_locking=self._use_locking)

  def _resource_apply_sparse_duplicate_indices(self, grad, var, indices,
                                               **kwargs):
    if self._momentum:
      return super(SGD, self)._resource_apply_sparse_duplicate_indices(
          grad, var, indices, **kwargs)
    else:
      var_device, var_dtype = var.device, var.dtype.base_dtype
      coefficients = (kwargs.get("apply_state", {}).get((var_device, var_dtype))
                      or self._fallback_apply_state(var_device, var_dtype))

      return gen_resource_variable_ops.ResourceScatterAdd(
          resource=var.handle,
          indices=indices,
          updates=-grad * coefficients["lr_t"])

  def _resource_apply_sparse(self, grad, var, indices, apply_state=None):
    # This method is only needed for momentum optimization.
    var_device, var_dtype = var.device, var.dtype.base_dtype
    coefficients = ((apply_state or {}).get((var_device, var_dtype))
                    or self._fallback_apply_state(var_device, var_dtype))

    momentum_var = self.get_slot(var, "momentum")
    return gen_training_ops.ResourceSparseApplyKerasMomentum(
        var=var.handle,
        accum=momentum_var.handle,
        lr=coefficients["lr_t"],
        grad=grad,
        indices=indices,
        momentum=coefficients["momentum"],
        use_locking=self._use_locking,
        use_nesterov=self.nesterov)

  def get_config(self):
    config = super(SGD, self).get_config()
    config.update({
        "learning_rate": self._serialize_hyperparameter("learning_rate"),
        "decay": self._serialize_hyperparameter("decay"),
        "momentum": self._serialize_hyperparameter("momentum"),
        "nesterov": self.nesterov,
    })
    return config

当动量为0时，参数w的更新规则（梯度为g）：

w = w - 学习率 * g

当动量大于0时的更新规则：

速度 = 动量 * 速度 - 学习率 * g
w = w + 速度

当`nesterov=True`时（即采用Nesterov动量），此规则变为：

速度 = 动量 * 速度 - 学习率 * g
w = w + 动量 * 速度 - 学习率 * g

参数：

学习率
动量：浮点超参数 >=0，加速梯度下降在相关方向并抑制振荡。
nesterov：布尔值，是否应用Nesterov动量
name：可选名称前缀，用于应用梯度时创建的操作。默认为`"SGD"。
kwargs：关键字参数。允许是 `"clipnorm"或`"clipvalue"之一。 `"clipnorm"（浮点）按范数裁剪梯度；`"clipvalue"（浮点）按值裁剪梯度。

用法:

这段代码展示了如何使用 TensorFlow 中的 SGD（随机梯度下降）优化器进行基本的优化步骤。这里通过一个简单的二次函数 loss = (var ** 2) / 2.0 来演示优化过程，其中 var 是一个 TensorFlow 变量，初始值为 1.0。梯度下降的目标是通过调整 var 的值来最小化损失函数。

  >>> opt = tf.keras.optimizers.SGD(learning_rate=0.1) # 创建一个 SGD 优化器实例，学习率设置为 0.1
  >>> var = tf.Variable(1.0) # 定义一个 TensorFlow 变量 var，初始值为 1.0
  >>> loss = lambda: (var ** 2)/2.0  # 损失函数的梯度（导数）为 d(loss)/d(var) = var
  >>> step_count = opt.minimize(loss, [var]).numpy()   # 步长是 ：- 学习率 * 梯度
# 使用 SGD 优化器的 minimize 方法来执行一次优化步骤。
# 这一步计算损失函数关于 var 的梯度，并根据梯度和学习率更新 var 的值。  
  >>> var.numpy()
  0.9

打印更新后的 var 值，期望看到 var 值减少，因为损失函数关于 var 是正相关的。

带动量的SGD:

>>> opt = tf.keras.optimizers.SGD(learning_rate=0.1, momentum=0.9) #带动量的 SGD 优化器实例
  >>> var = tf.Variable(1.0)
  >>> val0 = var.value()
  >>> loss = lambda: (var ** 2)/2.0         # d(loss)/d(var1) = var1
  >>> # First step is `- learning_rate * grad`
  >>> step_count = opt.minimize(loss, [var]).numpy() #执行优化步骤
  >>> val1 = var.value()
  >>> (val0 - val1).numpy()
  0.1

更新公式为： new_var=var−learning_rate×var，所以 new_var=1.0−0.1×1.0=0.9。比较带动量优化前后 var 的值，由于动量的影响，期望看到更新步长增加。1.0−0.9=0.1

后续步骤中步长的增加：

  >>> # On later steps, step-size increases because of momentum
  >>> step_count = opt.minimize(loss, [var]).numpy()
  >>> val2 = var.value()
  >>> (val1 - val2).numpy()
  0.18

再次执行优化步骤，并比较连续两次更新的步长，由于动量的累积效应，步长应该进一步增加。