Universal scaling hypothesis of quantum spatial search in complex networks-CSDN博客

本文链接：https://blog.csdn.net/weixin_54703767/article/details/147248143

复杂网络中量子空间搜索的通用缩放假设

原文地址：https://journals.aps.org/prresearch/pdf/10.1103/PhysRevResearch.6.043119
在这里插入图片描述

概念：

坍缩图：是一种用于分析复杂网络中某些特征或参数变化的可视化工具。它通常用于展示网络在某种操作或变化下的行为模式。例如，在研究网络的鲁棒性或动态变化时，坍缩图可以用来展示网络在不同条件下的崩溃规模分布。在复杂网络的量子搜索问题中，坍缩图可以用于展示最优时间、最大发现概率和最优跃迁参数之间的关系。在很多物理系统中，不同参数下的原始数据看起来很不一样。但如果你使用恰当的归一化或变换方法，把某些变量按某种规律缩放后，会发现这些数据点可以“塌缩（collapse）”在一条或几条统一的曲线上。

这种现象说明：不同参数下的系统，其行为是相似的，只是尺度不同。

**基于路径的积分方法（Path Integral Method）：**路径积分方法是一种量子力学和量子场论中的重要工具，用于计算粒子从一个位置到另一个位置的概率振幅。它基于费曼的路径积分表述，认为粒子在从起点到终点的过程中会经历所有可能的路径，每条路径都有一个对应的相位因子。在复杂网络的量子行走问题中，路径积分方法可以用来确定连续时间量子行走中概率振幅与路径长度分布之间的关系。这种方法通过考虑所有可能的路径来计算粒子在复杂网络中的传播行为，从而揭示网络的量子特性。

摘要

拟解决问题：

量子空间算法中是否存在适用于各种网络的通用视角

贡献：

提出一个通用的缩放假设：在复杂网络上进行量子空间搜索；
阐明连续时间量子又走中的概率幅度可以由路径铲毒分布决定。

引言

量子应用于网络科学：

量子随机网络【25】

量子传感网络【26、27】

量子通信【28】

纠缠渗透【29、30】

量子互联网【31-34】

网络科学应用于量子：

量子相变【35】

时间晶体【36】

定位/离域【37、38】

机器学习领域：

量子游走在图上性能由于经典随机游走【59、60】

例如：

涉及节点标签或类别的节点分类已被经典算法广泛探索 [61，64]。
在无标度网络上的随机游走采样算法降低了图的学习成本 [63， 64]。
量子游走作为随机游走的量子对应物，也被研究用于学习图表示。
量子游走可以比经典方法更准确地学习这些表示 [60]。

但是，在网络（例如无标度网络和小世界网络）上进行空间搜索的时间复杂度需要进一步研究。这就提出了一个问题，即这些复杂网络的算法中是否存在量子动力学的普遍视角，从而可能为量子系统和算法提供重要见解。

常规分析对于一些具有特点的网络具有一定的作用，但是对于获得普遍视角毫无用处。

Method

在一个N维希尔伯特空间内，对于无权图G(V, E)和带权图G(V,E,W)上的连续时间上，状态|i>对应节点标签i = 1, 2,…, N。这里的G都是联通无向图，包含N个顶点，且没有自环。量子空间搜索通过利用时间无关的哈密顿量 $\hat{H}=\hat{H}_L + \hat{H}w$ 的薛定谔动力方程来实现。

其中$ \hat{H}_w$ 是由oracle term（预言机？） $\hat{H}_w \equiv -\gamma_w |w\rangle \langle w|$ 给出的，（其中w是目标节点， $\gamma_w$ 是一个正实数， $\gamma_w$ 在本文中已经被归一化，也就是说$ \gamma_w=1$）

Difusion（or hoping）term $ \hat{H}L$ 被定义为$ \hat{H}L \equiv \gamma \hat{L}$ ，（$ \gamma$ 还是正数，$ \hat{L} $是拉普拉斯算子$ \hat{L} \equiv \hat{D} - \hat{A} $，其中$ \hat{A}\equiv\sum{i,j}A{ij}|i\rangle \langle j| $是加权邻接运算符，$ \hat{D}\equiv\sum_id_i|i\rangle \langle i| $是加权节点度运算符，其中加权节点度$ d_i $是连接到节点 i 的边的权重之和，即$ d_i\equiv \sum_jA_{ij}$）

对于无权图的量子搜索，我们采用所有边的权重 $A_{ij}=0or1$ ，其值取决于哦木感兴趣的网络结构。对于加权图，我们将无权图量子搜索中的权重 $A_{ij}$ 替换为从区间（0,1）上的均匀分布。

量子空间搜索的初始状态是一个均匀叠加态，表示为 $\left| s \right\rangle = \sum_{i=1}^{N} \left| i \right\rangle / \sqrt{N}$ 。在时间t时，目标节点w上的发现概率 $\, = \, \left| \langle w | \, e^{-i\hat{H}t} \, | s \rangle \right|^2$

在量子空间搜索中，跳跃参数 γ 被优化，以最大化发现概率的峰值。这个条件与|s>和哈密顿量 $\hat{H}$ 的基态 $|E_0\rangle$ 之间的重叠度与第一激发态 $|E1\rangle$ 之间的重叠度的条件相对应，即 $|\langle s|E_0 \rangle|^2=|\langle s|E_1 \rangle|\sim0.5$ 。（为了使量子搜索最有效，初始状态应该和哈密顿量的基态和第一激发态之间的重叠度相等。）通过使用这个最优的 γ，我们确定最优的发现概率 P 以及最优的时间 $t = Q$ ，分别给出发现概率的峰值和峰-峰周期。

在这里插入图片描述
如果用传统方式(即
假设)来分析这些网络结构上的量子搜索算法，是得不到普适性规律的。
左侧: fractal-β 模型[(a)-©]横轴都是节点数 N，纵轴是

(a) $\gamma$ ( $\beta$ ):最优跳跃参数

(b)Q( $\beta$ ):最优搜索时间

©P( $\beta$ ):搜索成功概率

特点:

对于B=0(黑色点)， $\gamma$ 、Q和P呈现出明确的幂律关系，几乎是直线(对数坐标下)→所以能用 O(N^a) 表达。
但当 $\beta$ ≠0(比如 $\beta$ =0.02,0.08,1.0)，这些关系变得不再是严格幂律，说明不适用传统标度分析，
$\beta$ 越大，系统越接近随机图，P趋于稳定，而y的增长速度减缓

右侧: WS 模型[(d)-(f)]

网络也从规则图(B=0)逐渐演化为小世界图甚至随机图(B=1.0)

但和 fractal-β 模型不同的是，y, Q,P对于不同 β值几乎都是横向平行的线条，也就是说，对数标度下几乎是常数，没有明显的幂律关系。

这说明在 WS 模型中，网络的复杂性对搜索性能的影响比 fractal-B模型小很多。

这些参数严重依赖于网络的拓扑特性和 $\beta$ 值。

这在 fractal- $\beta$ 模型中表现得尤其明显(只在 $\beta$ =0时近似幂律)而 WS 模型中几乎都是平稳的。

所以说，如果你想在不同网络之间寻找“统一的规律”，用传统幂律的方法不行，必须引入新的视角。
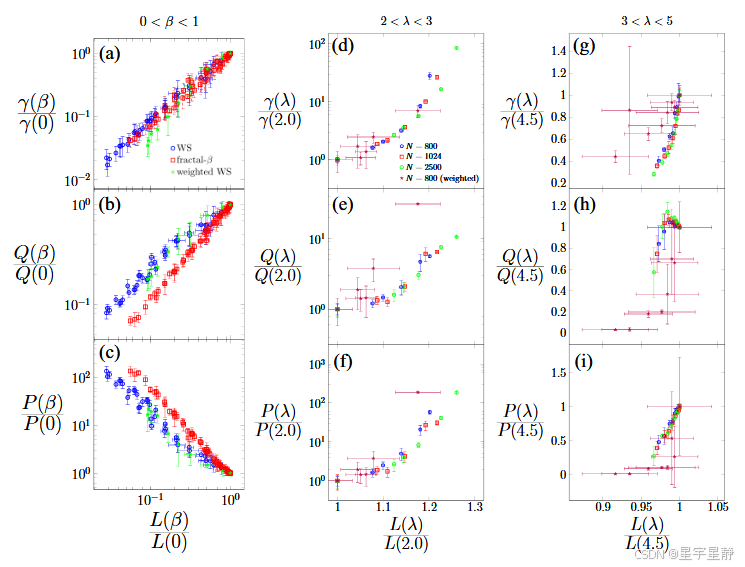
在这里插入图片描述

图(a) - （c)：WS和fractal-β模型（小世界网络）

范围： $0 < β < 1$ ，在 WS 小世界模型和 fractal-β 模型中变化。
观察点：
- 多组不同节点数 $N$ 的结果几乎重合，说明存在普适行为。
- 图(a)：γ 随 L 增大而增长（对数坐标）。
- 图(b)：Q 随 L 增大而增长（与γ类似）。
- 图（c)：P 随 L 增大而下降，表明平均路径变长时成功率降低。
结论： 明确揭示了物理量与平均路径长度的幂律关系，并验证了三条公式：

$\frac{γ(β)}{γ(0)} = \left(\frac{L(β)}{L(0)}\right)^{α_γ}, \quad \frac{Q(β)}{Q(0)} = \left(\frac{L(β)}{L(0)}\right)^{α_Q}, \quad \frac{P(β)}{P(0)} = \left(\frac{L(β)}{L(0)}\right)^{α_P}$
- $α_γ = 1.08(6)，α_Q = 0.90(5)，α_P = -1.76(8)$

图(d)-(f)：Scale-Free 网络，2 < λ < 3

范围： 幂律指数 $\in (2, 3)$ ，表示是尺度无关网络（许多中心节点存在）。
图(d)-(f)：类似的幂律行为仍然存在，尽管不再是简单的 WS 网络。
- 各种节点数量 $N$ 仍然成功“塌缩”到一条曲线，说明数据结构相似。
- 权重对塌缩图影响较小。
结论： 在 scale-free 网络中，只要 $λ$ 在 $(2, 3)$ 范围内，仍然可以使用平均路径长度生成 collapse plots。

图(g)-(i)：随机网络，λ > 3

观察点：
- 数据非常分散，塌缩图不再明显。
- 权重和节点数影响显著。
结论：
- 平均路径长度不再主导物理量行为。
- 网络结构变得更“随机”，没有中心节点或清晰结构。
- γ, Q, P 对平均路径的依赖变弱甚至消失。

虽然还没有严格的数学证明，但从量子波函数传播和干涉的物理角度来看，平均路径长度对量子搜索结果的影响是有逻辑依据的——路径长度分布越广，波函数越容易在目标节点集中，搜索成功率就越高。

实现步骤

这一思想可以通过概率振幅与路径长度分布之间的一个明确关系来支持。考虑量子空间搜索中的概率振幅 π，其表达式为 $〈w|e^{−i\hat{H}t}|s〉$ 〉。我们将哈密顿量 H 分为两个部分：H = ĤL + Ĥw，并进一步写作 H ≡ ĤA + Ĥd，其中

ĤA ≡ −γÂ（图的邻接矩阵 Â）
Ĥd ≡ −∑ᵢ Γᵢ|i⟩⟨i|，其中 Γᵢ ≡ γwδᵢ,ʷ − γdᵢ

按照路径积分形式的 Suzuki-Trotter 分解方法，有：

$\lim_{M→∞} \langle w | \left(e^{-i\hat{H}_A t/M} e^{-i\hat{H}_d t/M} \right)^M | s \rangle$

概率振幅 π 可以分解成一个核函数：

$K_M(i, j; t) ≡ \langle i | e^{-i\hat{H}_A t/M} e^{-i\hat{H}_d t/M} | j \rangle$

该核可被简化为：

$K_M(i, j; t) = e^{iΓ_j t/M} \sum_{n=0}^{\infty} \frac{1}{n!} \left( \frac{iγt}{M} \right)^n f_n(i,j)$

其中

$f_n(i,j) ≡ \langle i | \hat{A}^n | j \rangle$

因此，概率振幅最终可以表示为：

$\lim_{M→∞} \prod_{m=1}^{M} \sum_{i_m=1}^{N} \sum_{n_m=0}^{\infty} C_{M}^{(n_m,i_m)}(t) \cdot \frac{1}{\sqrt{N}} f_{n_m}(i_{m-1}, i_m)$

其中 $C_M^{(n_m,i_m)}(t)$ 是前面核的系数项。

根据路径积分形式，每个 Trotter 时间片中出现网络结构，节点之间的跳跃发生在相邻的时间片之间，并通过函数 $f_{n_m}(i_{m-1}, i_m)$ 表示。特别地，对于无权图，fₙ(i, j) 就是从节点 j 到节点 i 的路径长度为 n 的路径数量，也即路径长度分布。正式建立了“网络结构 ↔ 搜索效率”的联系，路径越多、越丰富，则搜索更有效。

需要指出的是，概率振幅还可以通过格林函数形式与路径长度分布 Pₙ(i, j) 联系起来，其传播子为：

$G_i^0(ω) = \frac{1}{ω - γd_i + γwδ_{i,w}}$

图4展示了最优跳跃参数 γ 与发现概率 P之间的关系。数据来自不同的网络模型和实际网络，包括：

模型网络： 例如WS模型、扩展的WS模型、Sierpinski地毯、扩展的fractal-β模型等；
实际网络： 如合作作者网络、人类疾病网络、小鼠大脑网络等。
x轴： 最优跳跃参数 $\gamma$
y轴： 发现概率 $P$
数据点： 不同的模型和实际网络对应不同的符号和颜色。
拟合曲线： 实线和虚线分别对应不同的模型（例如D=1的实线和D=2.11的虚线）。

这个图揭示了发现概率 $P$ 随着跳跃参数 $\gamma$ 变化的规律，这些数据很好地拟合了以下关系：

$P(\gamma) = \frac{1}{A + (D\gamma + B)^C}$

其中拟合参数为 A = 0.991(1)，B = 0.086(5)，C = 1.68(2)。

Summary

综上所述，我们提出了复杂网络中量子空间搜索的通用缩放假设。使用 Watts-Strogatz 模型中的连续时间量子游走、分形β模型和静态无标度网络模型，涵盖了规则、随机、小世界和无标度网络，我们已经证明，作为平均路径长度的函数，坍缩图可以出现在发现概率、最佳时间以及最佳跳跃参数中。我们还利用路径积分形式建立了目标节点的概率幅值与路径长度分布之间的显式关系。复杂网络科学的思想在量子复杂网络系统中仍然有用，我们的结果为量子物理学和复杂网络科学之间的联系提供了新的见解。