浅谈稀疏性与压缩感知（二）

前言

接着前一部分所述，这一节介绍稀疏回归、稀疏表示、鲁棒主成分回归、稀疏传感器布置（Sparse Sensor Placement）等等。

5、稀疏回归

$l_1$范数可用于正则化统计回归，既可以惩罚统计异常值，又可以获得尽可能少的简化统计模型。
最小二乘回归是用于数据拟合的最常见的统计模型，但是容易被单个大的异常值破坏，因为与拟合线的距离是平方关系，所以异常值的权重更大。相对应，$l_1$最小解对所有数据给予相同的权重，使其对异常值和破坏的数据更具鲁棒性，此过程被称为最小绝对偏差（LAD），下面的例子显示了最小二乘回归和最小偏差回归的差别：

import numpy as np
import matplotlib.pyplot as plt
import os
from scipy.optimize import minimize


plt.rcParams['figure.figsize'] = [7, 7]
plt.rcParams.update({'font.size': 18})
x = np.sort(4*(np.random.rand(25,1)-0.5),axis=0) # Random data from [-2,2],从小到达排序
b = 0.9*x + 0.1*np.random.randn(len(x),1)  # 返回的结果是服从均值为0，方差为1的标准正态分布，而不是局限在0-1之间，也可以为负值
atrue = np.linalg.lstsq(x,b,rcond=None)[0] # 最小二乘 输出包括四部分：回归系数、残差平方和、自变量X的秩、X的奇异值。
atrue = atrue.item(0)#保留斜率k

b[-1] = -5.5  # Introduce outlier#增加异常值
aL2 = np.linalg.lstsq(x,b,rcond=None)[0] # New slope
aL2 = aL2.item(0)
plt.plot(x[:-1],b[:-1],'o',color='b',ms=8,label='Data') # Data
plt.plot(x[-1],b[-1],'o',color='r',ms=8,label='Outlier')   # Outlier  ms标记符大小

xgrid = np.arange(-2,2,0.01)
plt.plot(xgrid,atrue*xgrid,'--',linewidth=3,color='r',label='True Model')    # L2 fit (no outlier)
plt.plot(xgrid,aL2*xgrid,'--',linewidth=3,color='c',label='L2 fit') # L2 fit (outlier)

plt.legend()
plt.show()#包含异常值时L1的结果更稳定，L2偏差较大
## L1 optimization to reject outlier
def L1_norm(a):
    return np.linalg.norm(a*x-b,ord=1)

a0 = aL2   
res = minimize(L1_norm, a0)
aL1 = res.x[0]  # aL1 is robust
plt.plot(x[:-1],b[:-1],'o',color='b',ms=8,label='Data') # Data
plt.plot(x[-1],b[-1],'o',color='r',ms=8,label='Outlier')   # Outlier

xgrid = np.arange(-2,2,0.01)
plt.plot(xgrid,atrue*xgrid,'--',linewidth=3,color='r',label='True Model')    # L2 fit (no outlier)
plt.plot(xgrid,aL2*xgrid,'--',linewidth=3,color='c',label='L2 fit') # L2 fit (outlier)
plt.plot(xgrid,aL1*xgrid,'--',linewidth=3,color='k',label='L1 fit') # L1 fit (outlier)
plt.legend()
plt.show()#包含异常值时L1的结果更稳定，L2偏差较大

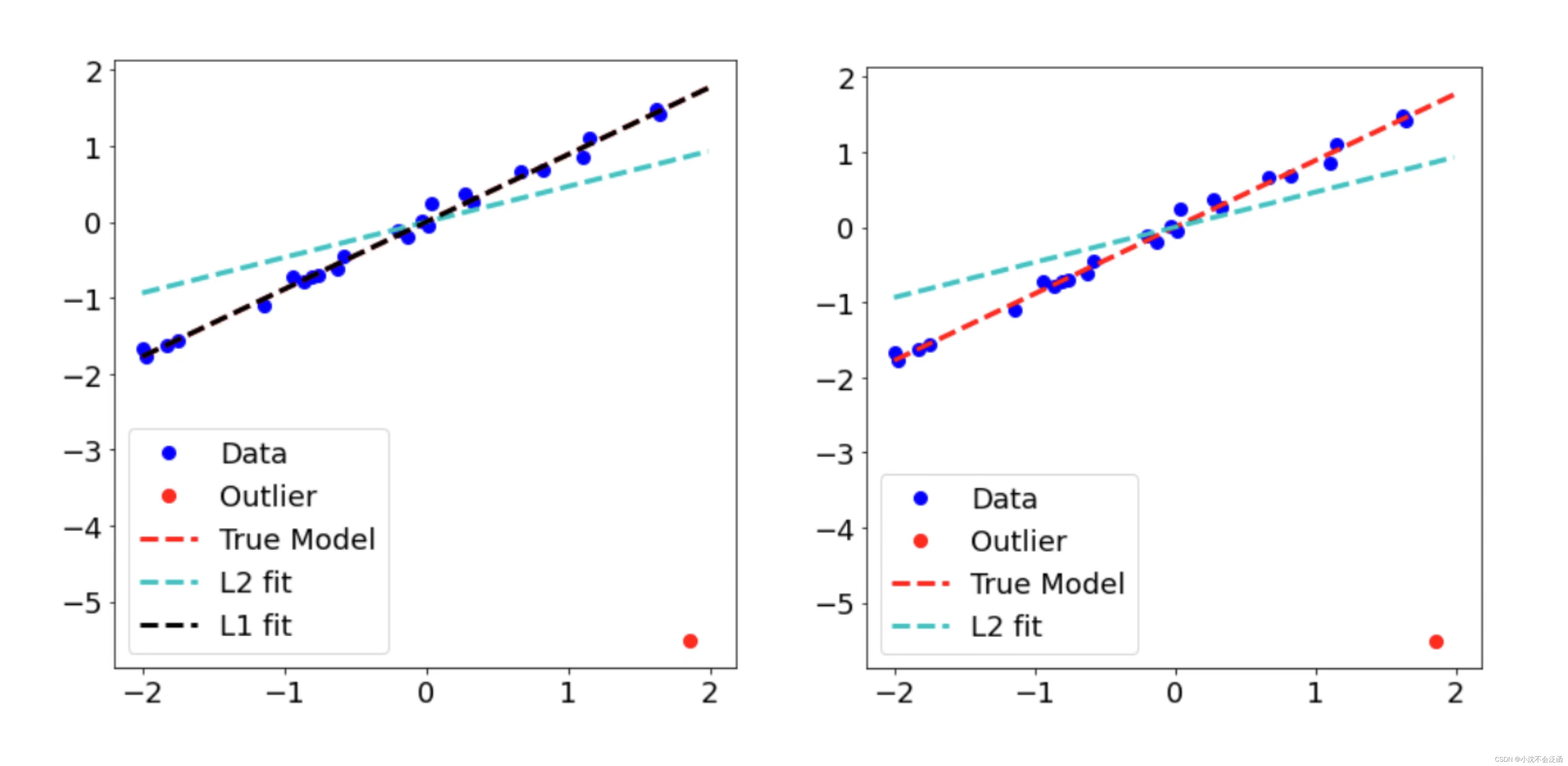
结果如上图，可见$l_1$最小范数解确实对异常值有很大的鲁棒性，在有无异常值的两种情况下几乎无差别。
下面介绍特征选择和LASSO回归，可解释性在统计模型中是很重要的，最小绝对收缩和选择算子（LASSO）是一种$l_1$惩罚回归技术，可在模型复杂性和描述能力之间取得平衡。
给定一个观测系统的若干预测值和输出值，按行排列成矩阵$A$和向量$b$，通过回归分析寻求$A$的列和$b$之间的相容关系，可以写成$Ax=b$，最小二乘回归往往导致向量$x$的所有项的系数都不为0，这意味着必须用$A$的所有列来预测$b$，但是我们通常认为统计模型应该更简单，即$x$是稀疏的。LASSO回归的损失函数为：$$\mathbf{x}=\underset{x^{\prime }}{\mathrm{argmin}}\Vert A{x}^{\prime }-b{\Vert }_2+\lambda \Vert x{\Vert }_1$$加入惩罚项的目的是防止过拟合，岭回归中的惩罚项是将上式中的$|x{\Vert }_1$换成$|x{\Vert }_2$，而弹性网络的惩罚项是${\lambda }_1\Vert x{\Vert }_1+{\lambda }_2\Vert x{\Vert }_2$。
LASSO回归中的$\lambda$在一系列值中变化，并且拟合在保留数据的测试集上。如果没有足够多的数据来提供充分多大的训练集和测试集，通常会在随机选择的情况下重复训练和测试模型，从而得到交叉验证的性能，此外LASSO回归可以很好的解决超定问题。
举一个简单的例子，$b$是100个输出观测值组成的列向量，$b$中的每个输出值由10个候选预测因子中的两个组合来给出，这些预测观测值按行排列成矩阵$A\in R^{100\times 10}$，向量$x$构造成稀疏的，并且向$b$中添加了噪声，通过构造训练集和测试集、交叉验证和网格搜索将均方误差（MSE）绘制为$\lambda$的函数：

import numpy as np
import matplotlib.pyplot as plt
import os
import scipy.io
from sklearn import linear_model
from sklearn import model_selection

plt.rcParams['figure.figsize'] = [7, 7]
plt.rcParams.update({'font.size': 18})
A = np.random.randn(100,10) # Matrix of possible predictors
x = np.array([0, 0, 1, 0, 0, 0, -1, 0, 0, 0]) #Two nonzero predictors
b = A @ x + 2*np.random.randn(100)

xL2 = np.linalg.pinv(A) @ b#最小二乘回归系数
reg = linear_model.LassoCV(cv=10).fit(A, b)#交叉验证次数，训练的x,y，LassoCV(eps=0.0001,n_alphas=300,cv=5).fit(xtrain,ytrain)

lasso = linear_model.Lasso(random_state=0, max_iter=10000)
alphas = np.logspace(-4, -0.5, 30)#产生等比数列，第一项是10的-4次方

tuned_parameters = [{'alpha': alphas}]#参数取值范围

clf = model_selection.GridSearchCV(lasso, tuned_parameters, cv=10, refit=False)#网格搜索
clf.fit(A, b)

scores = clf.cv_results_['mean_test_score']#均方误差
scores_std = clf.cv_results_['std_test_score']
plt.semilogx(alphas, scores,'r-')
# 绘制显示 +/- 标准误差的误差线
std_error = scores_std / np.sqrt(10)

plt.semilogx(alphas, scores + std_error, 'k--')
plt.semilogx(alphas, scores - std_error, 'k--')
plt.fill_between(alphas, scores + std_error, scores - std_error, alpha=0.1,color='k')#填充两条曲线之间， alpha=0.1表示透明度从0到1

plt.ylabel('CV score +/- std error')
plt.xlabel('alpha')
plt.axhline(np.max(scores), linestyle='--', color='.5')
plt.xlim([alphas[-1], alphas[0]])

plt.show()
alphas = np.logspace(-4, -0.5, 30)#产生等比数列，第一项是10的-4次方
XL1 = linear_model.Lasso(alpha=clf.best_params_['alpha'])
XL1.fit(A,b)
xL1 = XL1.coef_
xL1DeBiased = np.linalg.pinv(A[:,np.abs(xL1)>0]) @ b
xL1DeBiased

做出的图像应该是左侧的，但是运行此代码后却差强人意：

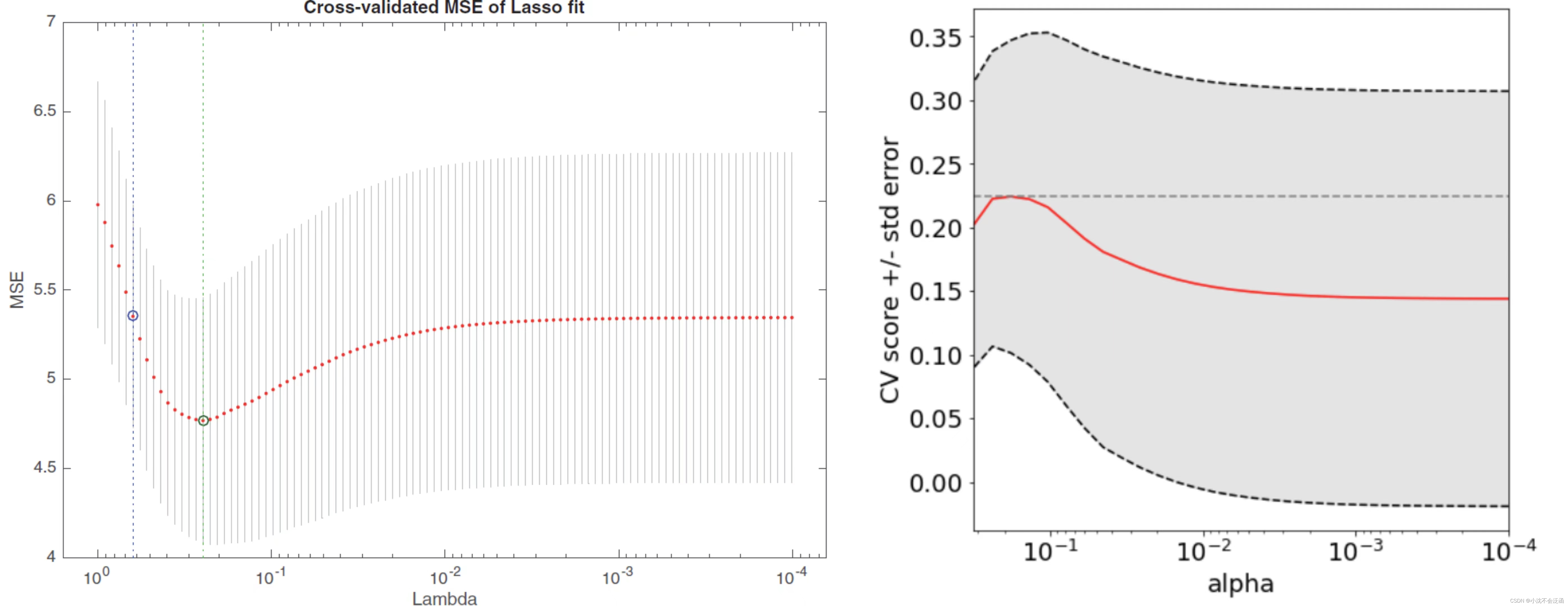
对于代码的修改感觉也无从下手，说白了不知道错误出在什么地方，对于正确的结果（对应重构的$x$）所得的$xL1$应该是稀疏的并且非零项的位置和大小应该很接近，但是这些项的回归值并不准确，有必要应用最小二乘回归对非零系数进行辨识，以此对LASSO回归去偏。（加粗的部分说实话我并没有理解缘由以及操作的原理）

6、稀疏表示

当高维信号表现出低维结构时，在适当的基或字典中，会出现稀疏表示，前几部分都是在傅里叶基上为例，这里在完备的字典上讨论，以特征脸为例，字典中的列由训练数据本身组成，使用人脸图像库构建超完备库$\Theta$，数据库中每一个人都使用30张图像，共有20个人，$\Theta$有600列，为了使用压缩感知，需要保证$\Theta$是欠定的，将每个图像的像素从192×168降采样到12×10，从而使每个图像变成120个成分的向量，当然这种降采样对分类的精度有影响，对于20个人中的某一个或几个人的图像（即为$c$类）降采样形成新的的测试图像，根据$y=\Theta s$使用压缩感知算法，所得向量$s$应该是稀疏的，理想情况下，在与$c$类对应的库中，该向量具有较大的系数（$s$为600行的列向量，在某连续的30行系数较大）。算法的分类阶段利用向量$s$中的每一类的系数（每30行）来计算$l_2$重构误差。大致的示意图如下：

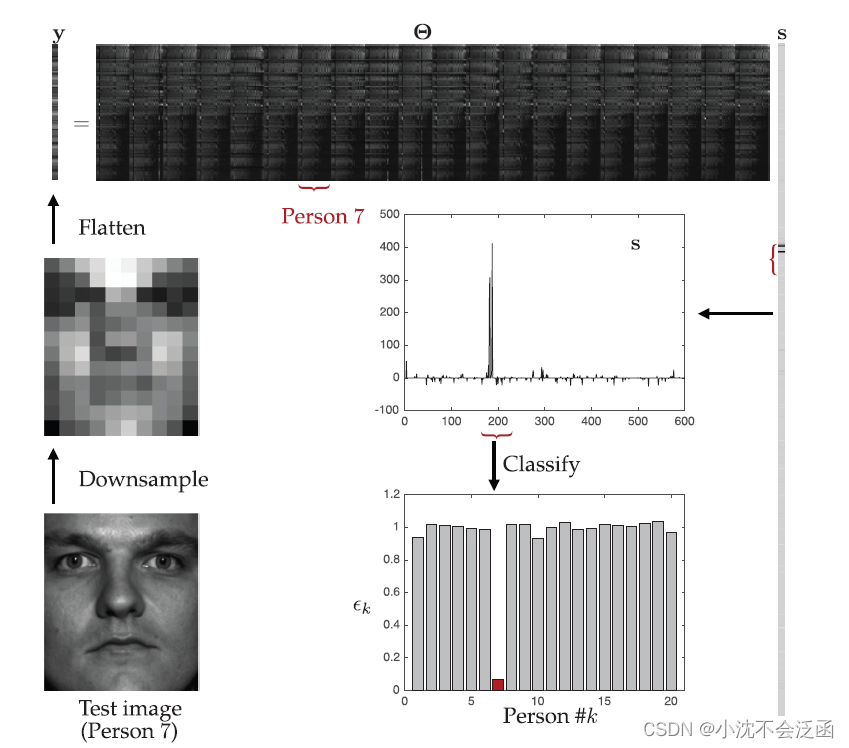
import numpy as np
import matplotlib.pyplot as plt
import os
import scipy.io
from sklearn import linear_model
from sklearn import model_selection
from scipy.optimize import minimize
from skimage.transform import resize
from matplotlib.image import imread


plt.rcParams['figure.figsize'] = [7, 7]
plt.rcParams.update({'font.size': 18})

mustache = imread(os.path.join('..','DATA','mustache.jpg'))
mustache = np.mean(mustache, -1); # 转化为灰度图像
mustache = (mustache/255).astype(int)#转化为整数类型
mustache = mustache.T#转置

mat = scipy.io.loadmat(os.path.join('..','DATA','allFaces.mat'))
X = mat['faces']#mat创建矩阵
nfaces = mat['nfaces'].reshape(-1)#转换成行向量
n = mat['n']##
n = int(n)
m = mat['m']
m = int(m)
#print(X.shape)=(32256, 2410)，m=168,n=192
## 构建训练集和测试集
nTrain = 30
nTest = 20
nPeople = 20
Train = np.zeros((X.shape[0],nTrain*nPeople))#X行数×600的元素为0的矩阵
Test = np.zeros((X.shape[0],nTest*nPeople))

for k in range(nPeople):
    baseind = 0
    if k > 0:
        baseind = np.sum(nfaces[:k])
    inds = range(baseind,baseind+nfaces[k])
    Train[:,k*nTrain:(k+1)*nTrain] = X[:,inds[:nTrain]]
    Test[:,k*nTest:(k+1)*nTest] = X[:,inds[nTrain:(nTrain+nTest)]]
## 降采样训练(建立完备 Theta库)
M = Train.shape[1]#训练集的列数=600

Theta = np.zeros((120,M))
for k in range(M):
    temp = np.reshape(np.copy(Train[:,k]),(m,n))
    tempSmall = resize(temp, (10, 12), anti_aliasing=True)
    Theta[:,k] = np.reshape(tempSmall,(1,120))
## 标准化Theta列
normTheta = np.zeros(M)
for k in range(M):
    normTheta[k] = np.linalg.norm(Theta[:,k])
    Theta[:,k] = Theta[:,k]/normTheta[k]
## 构建4个测试图像 (Test[:,125] = test image 6, person 7)
x1 = np.copy(Test[:,125]) # 干净的测试图像
x2 = np.copy(Test[:,125]) * mustache.reshape(n*m)#胡须遮挡的
randvec = np.random.permutation(n*m)
first30 = randvec[:int(np.floor(0.3*len(randvec)))]
vals30 = (255*np.random.rand(*first30.shape)).astype(int)
x3 = np.copy(x1)
x3[first30] = vals30 # 30%遮挡像素的图像
x4 = np.copy(x1) + 50*np.random.randn(*x1.shape) # 图像添加噪声
## 下采样测试图像
X = np.zeros((x1.shape[0],4))
X[:,0] = x1
X[:,1] = x2
X[:,2] = x3
X[:,3] = x4

Y = np.zeros((120,4))
for k in range(4):
    temp = np.reshape(np.copy(X[:,k]),(m,n))
    tempSmall = resize(temp, (10, 12), anti_aliasing=True)
    Y[:,k] = np.reshape(tempSmall,(1,120))
## L1 Search, 干净图像
y1 = np.copy(Y[:,0]) 
eps = 0.01

# L1 Minimum norm solution s_L1
def L1_norm(x):
    return np.linalg.norm(x,ord=1)

constr = ({'type': 'ineq', 'fun': lambda x:  eps - np.linalg.norm(Theta @ x - y1,2)})#不等条件，默认大于等于0  ，误差小于0.01
x0 = np.linalg.pinv(Theta) @ y1 # initialize with L2 solution
res = minimize(L1_norm, x0, method='SLSQP',constraints=constr)
s1 = res.x
plt.figure()
plt.plot(s1)#稀疏向量s
plt.figure()
plt.imshow(np.reshape(Train @ (s1/normTheta),(m,n)).T,cmap='gray')
plt.figure()
plt.imshow(np.reshape(x1 - Train @ (s1/normTheta),(m,n)).T,cmap='gray')

binErr = np.zeros(nPeople)
for k in range(nPeople):
    L = range(k*nTrain,(k+1)*nTrain)
    binErr[k] = np.linalg.norm(x1-Train[:,L] @ (s1[L]/normTheta[L]))/np.linalg.norm(x1)#x1-第k个人对应的s的系数*训练集中第k个人的图像信息，
    #重构的的越接近测试图像则对应这类的误差最小
    
plt.figure()
plt.bar(range(nPeople),binErr)
plt.show()

算法的分类阶段选用了干净的图像、假胡须遮挡、30%像素遮挡、添加白噪声四个图像测试，从最后的的分类结果上看效果还是不错的。

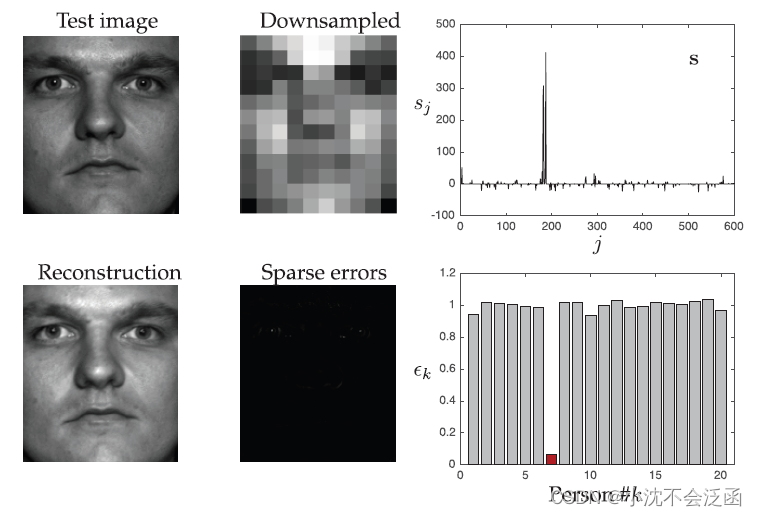
七、鲁棒主成分分析

前文所述最小二乘回归模型极易受到异常纸盒缺失数据的的影响，主成分分析也有同样的缺点，使其在异常值方面非常脆弱，为了改善这种敏感性，产生了鲁棒主成分分析（RPCA）方法，将数据矩阵$X$分解为结构化的低秩矩阵$L$和包含异常值和缺失数据的稀疏矩阵$S$：
$$X=L+S$$$L$的主成分对$S$中的异常值和缺失数据具有鲁棒性。
从数学上讲，RPCA的目标是找到满足以下条件的$L$和$S$：$$\underset{\mathrm{L},\mathrm{S}}{\min }\mathrm{rank}(L)+\Vert S{\Vert }_0\mathrm{subject}\mathrm{to}L+S=X.$$然而矩阵的秩和0范数都不是凸的（凸指的是凸函数，矩阵的秩可以考虑2×2的特例，0范数上一篇提到），这不是一个容易处理的优化问题，与压缩感知问题类似，可以使用松弛关系将上式转化为：$$\underset{\mathrm{L},\mathrm{S}}{\min }\Vert \mathbf{L}{\Vert }_{\ast }+\lambda \Vert S{\Vert }_1\mathrm{subject}\mathrm{to}L+S=X.$$其中$|\mathbf{L}{\Vert }_{\ast }$表示核范数，由奇异值的和给出，它也代表秩的大小。
如果$\lambda =1/\sqrt{\max (n,m)}$，其中$n$和$m$是$X$的维度，假定$L$和$S$满足以下条件：
1、$L$不是稀疏的；
2、$S$不是低秩的，假设各元素是随机分布的，没有低维的列空间。
则松弛后的解可以在高概率下收敛到非凸的问题的解。
具体算法如下：构造增光拉格朗日算子$$\mathcal{L}(L,S,Y)=\Vert L{\Vert }_{\ast }+\lambda \Vert S{\Vert }_1+⟨Y,X-L-S⟩+\frac{\mu }{2}\Vert X-L-S{\Vert }_F^2.$$求解使$\mathcal{L}$最小的$L_k$和$S_k$，更新拉格朗日乘子${\mathbf{Y}}_{k+1}={\mathbf{Y}}_k+\mu \left(\mathbf{X}-{\mathbf{L}}_k-{\mathbf{S}}_k\right)$然后一直迭代至收敛，在具体实现过程中需要构造收缩算子和奇异值阈值算子，在特征脸示例对此进行演示：

import numpy as np
import matplotlib.pyplot as plt
import os
import scipy.io

plt.rcParams['figure.figsize'] = [7, 7]
plt.rcParams.update({'font.size': 18})

mat = scipy.io.loadmat(os.path.join('..','DATA','allFaces.mat'))
faces = mat['faces']
nfaces = mat['nfaces'].reshape(-1)
## 定义收缩算子，奇异值阈值算子，RPCA

def shrink(X,tau):
    Y = np.abs(X)-tau
    return np.sign(X) * np.maximum(Y,np.zeros_like(Y))
def SVT(X,tau):
    U,S,VT = np.linalg.svd(X,full_matrices=0)
    out = U @ np.diag(shrink(S,tau)) @ VT
    return out
def RPCA(X):
    n1,n2 = X.shape
    mu = n1*n2/(4*np.sum(np.abs(X.reshape(-1))))
    lambd = 1/np.sqrt(np.maximum(n1,n2))
    thresh = 10**(-7) * np.linalg.norm(X)
    
    S = np.zeros_like(X)
    Y = np.zeros_like(X)
    L = np.zeros_like(X)
    count = 0
    while (np.linalg.norm(X-L-S) > thresh) and (count < 1000):
        L = SVT(X-S+(1/mu)*Y,1/mu)
        S = shrink(X-L+(1/mu)*Y,lambd/mu)
        Y = Y + mu*(X-L-S)
        count += 1
    return L,S
X = faces[:,:nfaces[0]]
L,S = RPCA(X)
inds = (3,4,14,15,17,18,19,20,21,32,43)

for k in inds:
    fig,axs = plt.subplots(2,2)
    axs = axs.reshape(-1)
    axs[0].imshow(np.reshape(X[:,k-1],(168,192)).T,cmap='gray')
    axs[0].set_title('X')
    axs[1].imshow(np.reshape(L[:,k-1],(168,192)).T,cmap='gray')
    axs[1].set_title('L')
    axs[2].imshow(np.reshape(S[:,k-1],(168,192)).T,cmap='gray')
    axs[2].set_title('S')
    for ax in axs:
        ax.axis('off')

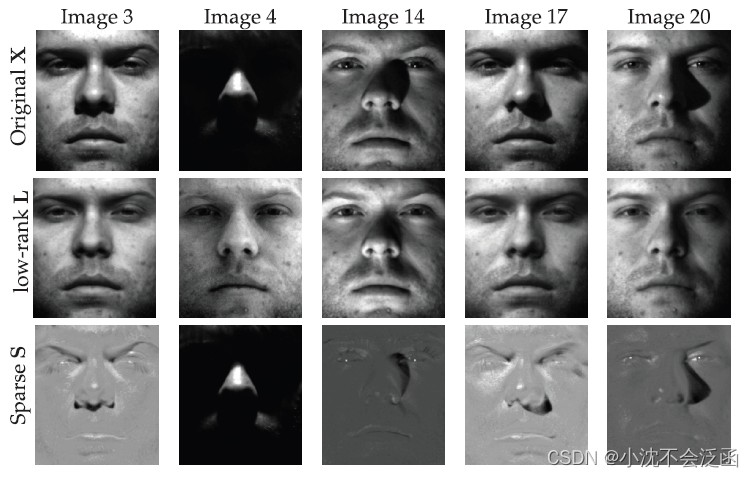
在此例中，$X$的原始列及其低阶和稀疏分量如图所示，RPCA有效地填充了与阴影相对应的图像遮挡区域。

8、稀疏传感器布置

首先我对这个题目也是有点疑惑，并没有确切的理解所谓的传感器到底指的是什么，书中提到包含重构和分类的传感器布置，涉及其他零碎的知识但又感觉没有什么实实在在的东西，只能说自己知识浅薄，目前还没看太懂，以后有机会再来补充吧。