高数复习系列（同济、b版）—— 快乐重积分

目录

前言

解题思路（无题）

一、二重积分计算

二、累次积分交换次序及计算

三、三重积分计算

---

前言

虽然该篇标题和以前一样属于快乐系列，但是笔者认为重积分的难度还是偏高的，尤其是笔者最近做了不少笔者觉得噩梦难度的题目（又爱又恨555）

重积分笔者觉得，难点在于积分域和计算，积分域关系到重积分计算的难度，而计算则是因为重积分可以算是多个一元积分的累积分，嵌套，因此很多题目还是会考验到学生的计算能力和技巧。

话不多说，老规矩

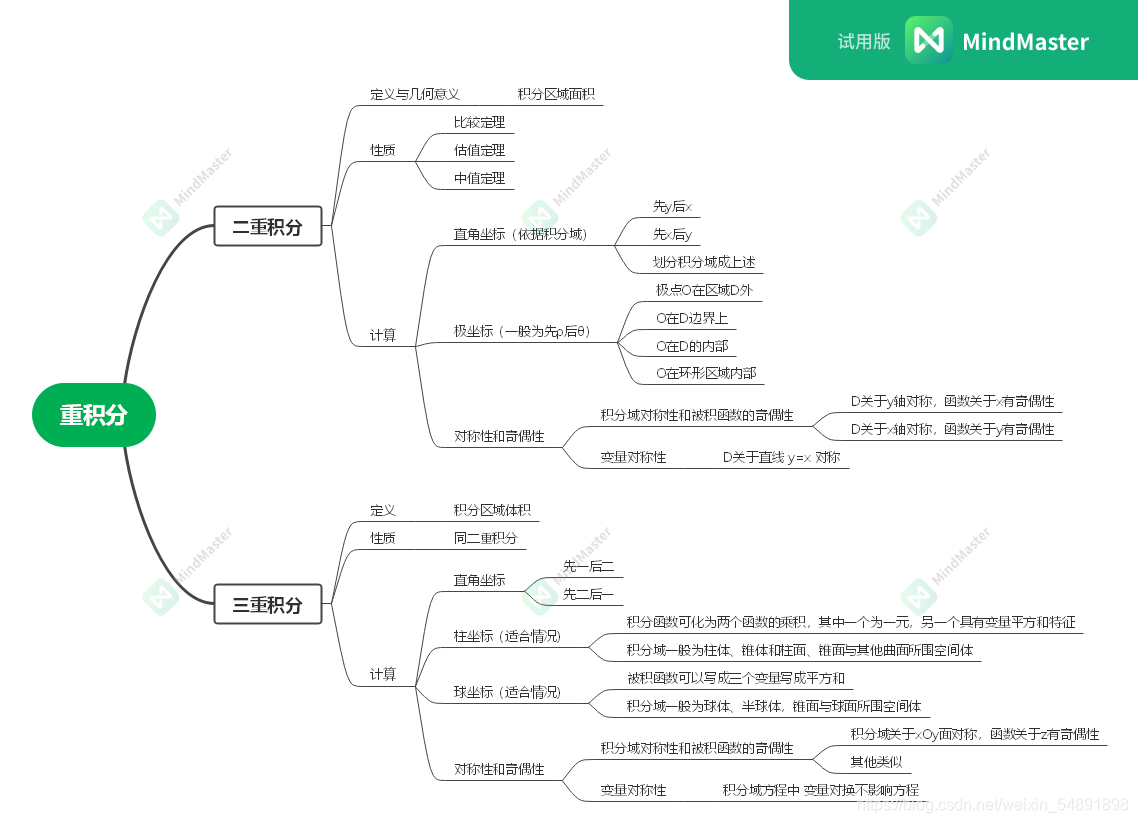
这次依旧没有题目噢，（笔者太懒了，还得准备考试）

解题思路（无题）

一、二重积分计算

1、画出积分域草图、判断积分域是否有对称性、被积函数是否具有奇偶性，进行对应的计算和化简

2、根据积分域的形状和被积函数形式选择坐标系

3、选择累次积分的次序

4、确定积分限然后计算

二、累次积分交换次序及计算

1. 累次积分交换次序

1）由积分限确定积分域

2）画出积分域草图

3）计算交换次序后的积分限然后做累次积分计算

三、三重积分计算

大体思路基本同二重积分，值得注意的是如果才用直角坐标系的时候，可以根据积分域形状判断采取先一后二还是先二后一，而柱坐标的形式基本和二重积分的极坐标相同，球坐标则会多引入一个角变量，同时多出的半径会比极坐标多一次，即二次。