图的概念
有向图
若 E E E 是有向边(也称弧)的有限集合时,则图 G G G 为有向图。弧是顶点的有序对,记为 < v , w > <v, w> <v,w>,其中 v , w v,w v,w 是顶点, v v v 称为弧尾, w w w 称为弧头, < v , w > <v,w> <v,w> 称为从顶点 v v v 到顶点 w w w 的弧,也称 v v v 邻接到 w w w ,或 w w w 邻接自 v v v 。

图( a a a)所示的有向图 G 1 G_1 G1 可表示为
G 1 = ( V 1 , E 1 ) G_1 = (V_1,E_1) G1=(V1,E1) V 1 = ( 1 , 2 , 3 ) V_1 = (1, 2, 3) V1=(1,2,3) E 1 = ( < 1 , 2 > , < 2 , 1 > , < 2 , 3 > ) E_1 = (<1,2>,<2,1>,<2,3>) E1=(<1,2>,<2,1>,<2,3>)
无向图
若 E E E 是无向边(简称边)的有限集合时,则图 G G G 为无向图。边是顶点的无序对,记为 ( v , w ) (v, w) (v,w) 或 ( w , v ) (w,v) (w,v) ,因为 ( v , w ) = ( w , v ) (v,w)=(w,v) (v,w)=(w,v), 其中 $ v,w$ 是顶点。可以说顶点 w w w 和顶点 v v v 互为邻接点。边 ( v , w ) (v, w) (v,w) 依附于顶点 w w w 和 v v v ,或者说边 ( v , w ) (v, w) (v,w) 和顶点 v , w v, w v,w 相关联。
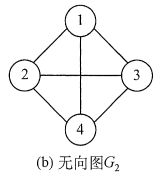
图( b b b)所示的无向图 G 2 G_2 G2 可表示为
G
2
=
(
V
2
,
E
2
)
G_2=(V_2,E_2)
G2=(V2,E2)
V
2
=
(
1
,
2
,
3
,
4
)
V_2 =(1,2,3,4)
V2=(1,2,3,4)
E
2
=
(
(
1
,
2
)
,
(
1
,
3
)
,
(
1
,
4
)
,
(
2
,
3
)
,
(
2
,
4
)
,
(
3
,
4
)
)
E_2 =((1,2),(1,3),(1,4),(2,3),(2,4),(3,4))
E2=((1,2),(1,3),(1,4),(2,3),(2,4),(3,4))
简单图
满足条件:
1.不存在重复边
2.不存在顶点到自身的边
多重图
若图 G G G 中某两个结点之间的边数多于一条,又允许顶点通过同一条边和自己关联,则 G G G 为多重图。多重图的定义和简单图是相对的。
完全图
对于无向图, E E E 的取值范围是 0 0 0 到 n n n × \times × ( n − 1 ) / 2 ( n − 1 ) / 2 (n−1)/2 ,有 n n n × \times × ( n − 1 ) / 2 ( n − 1 ) / 2 (n−1)/2 条边的无向图称为完全图,在完全图中任意两个顶点之间都存在边。对于有向图, E E E 的取值范围是 0 0 0 到 n × ( n − 1 ) n\times ( n − 1 ) n×(n−1) ,有 n × ( n − 1 ) n\times ( n − 1 ) n×(n−1) 条弧的有向图称为有向完全图,在有向完全图中任意两个顶点之间都存在方向相反的两条弧。
图的存储
领接矩阵
图的邻接矩阵( A d j a c e n c y M a t r i x Adjacency Matrix AdjacencyMatrix) 存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
设图 G G G 有 n n n 个顶点,则邻接矩阵 A A A 是一个 n × n n \times n n×n 的方阵,定义为:
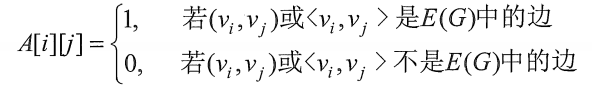
无向图和它的领接矩阵
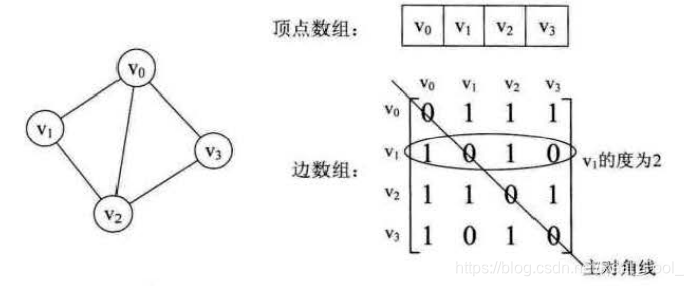
可以看出:
1.无向图的邻接矩阵一定是一个对称矩阵(即从矩阵的左上角到右下角的主对角线为轴,右上角的元与左下角相对应的元全都是相等的)。 因此,在实际存储邻接矩阵时只需存储上(或下)三角矩阵的元素。
2.对于无向图,邻接矩阵的第 i i i 行 ( 或第 i i i 列 ) 非零元素 ( 或非 ∞ ∞ ∞ 元素 ) 的个数正好是第 i i i 个顶点的度 T D ( v i ) TD (_{vi} ) TD(vi) 。比如顶点 v 1 v_1 v1 的度就是 1 + 0 + 1 + 0 = 2 1 + 0 + 1 + 0 = 2 1+0+1+0=2 。
3.求顶点 v i v_i vi 的所有邻接点就是将矩阵中第 i i i 行元素扫描一遍, A [ i ] [ j ] A [ i ] [ j ] A[i][j] 为 1 1 1 就是邻接点。
有向图和它的邻接矩阵:
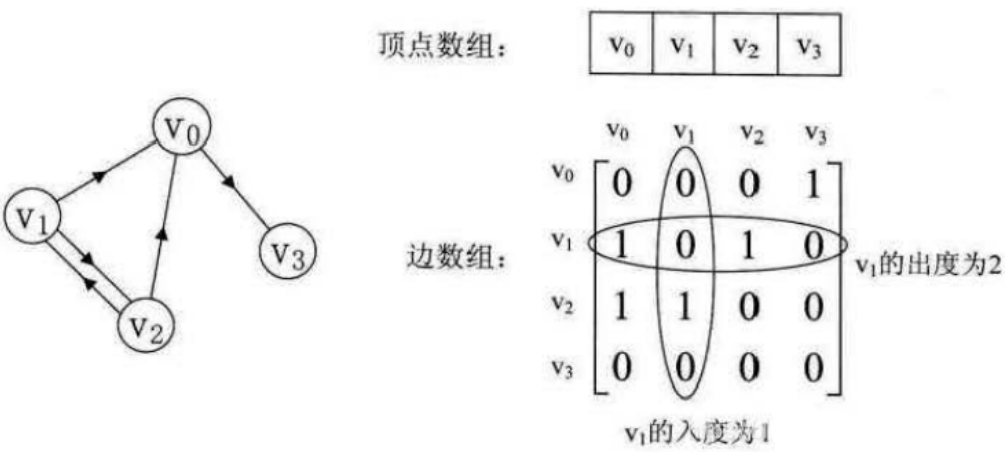
可以看出:
1.主对角线上数值依然为 0 0 0。但因为是有向图,所以此矩阵并不对称。
2.有向图讲究入度与出度,顶点 v 1 v_1 v1 的入度为 1 1 1 ,正好是第 v 1 v_1 v1 列各数之和。顶点 v 1 v_1 v1 的出度为 2 2 2 ,即第 v 1 v_1 v1 行的各数之和。
3.与无向图同样的办法,判断顶点 v i v_i vi 到 v j v_j vj 是否存在弧,只需要查找矩阵中 A [ i ] [ j ] A [ i ] [ j ] A[i][j] 是否为 1 1 1 即可。
最小生成树
P r i m Prim Prim 算法
思路: P r i m Prim Prim 算法基于贪心,我们每次总是选出一个离生成树距离最小的点去加入生成树,最后实现最小生成树。
public static int Prim(){
ArrayList<Integer> listU = new ArrayList<>();//已存入结点
ArrayList<Integer> listV = new ArrayList<>();//未存入结点
listU.add(0);
for(int i=1;i<n;i++){
listV.add(i);
}
double min;
int form = -1;//起点
int to = -1;//终点
double sum = 0;
while(!listV.isEmpty()) {
min = Double.MAX_VALUE;
for(int i:listU) {
for(int j:listV) {
if(edge[i][j]!=0 && edge[i][j]<min) {
min = edge[i][j];
form = i;
to = j;
}
}
}
if(min==Double.MAX_VALUE) {
System.out.println("-1");
return;
}
listU.add(to);
listV.remove(new Integer(to));
sum = sum + edge[form][to];
}
return sum;
}
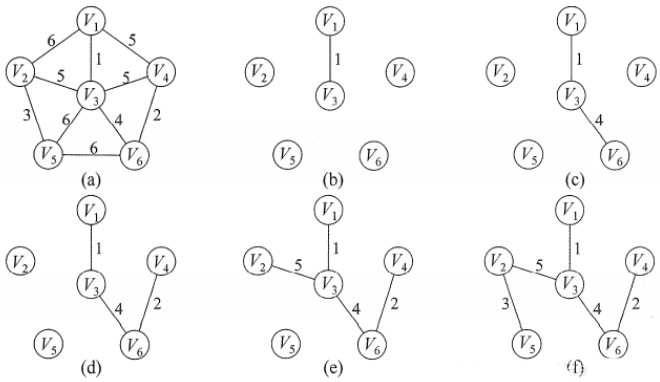
K r u s k a l Kruskal Kruskal 算法
思路:将图的存储结构使用边集数组的形式表示,并将边集数组按权值从小到大排序,遍历边集数组,每次选取一条边并判断是否构成环路,不会构成环路则将其加入最小生成树,最终只会包含 n − 1 n-1 n−1 条边 ( n n n 为无向图的顶点数 )。
import java.util.ArrayList;
import java.util.Collections;
//...数据读入包省略
public class Main{
public void static main(String[] args) {
//...数据读入省略
Collections.sort(list);
for(int i=0;i<list.size();i++) {
Edge e = list.get(i);
if(find(e.x)!=find(e.y)) {
merge(e.x,e.y);
num++;
ans = ans + e.w;
if(num==n-1) {
System.out.println(ans);//最小生成树边长之和
return;
}
}
}
}
static int find(int x) {
if(f[x] == x)
return f[x];
f[x] = find(f[x]);
return f[x];
}
static void merge(int x,int y) {
int xx = find(x);
int yy = find(y);
if(xx!=yy)
f[yy] = xx;
}
}
class Edge implements Comparable<Edge>{
int x;//起点
int y;//终点
int w;//边长
public Edge(int x, int y, int w) {
super();
this.x = x;
this.y = y;
this.w = w;
}
@Override
public int compareTo(Edge o) {
// TODO Auto-generated method stub
return this.w>o.w?1:-1;
}
}
例题:聪明的猴子
题目链接:聪明的猴子 - 蓝桥云课 (lanqiao.cn)

k r u s k a l kruskal kruskal 解法思路:
1.在构造最小生成树的过程中,找到所用的最长的一条边;
2.判断有几只猴子的跳跃距离>=最小生成树最长边;
样例分析:
4
1 2 3 4
6
0 0
1 0
1 2
-1 -1
-2 0
2 2
1.求出任意两棵树之间的距离,并且按照距离的大小进行排序,完成 f f f 数组初始化,得到;
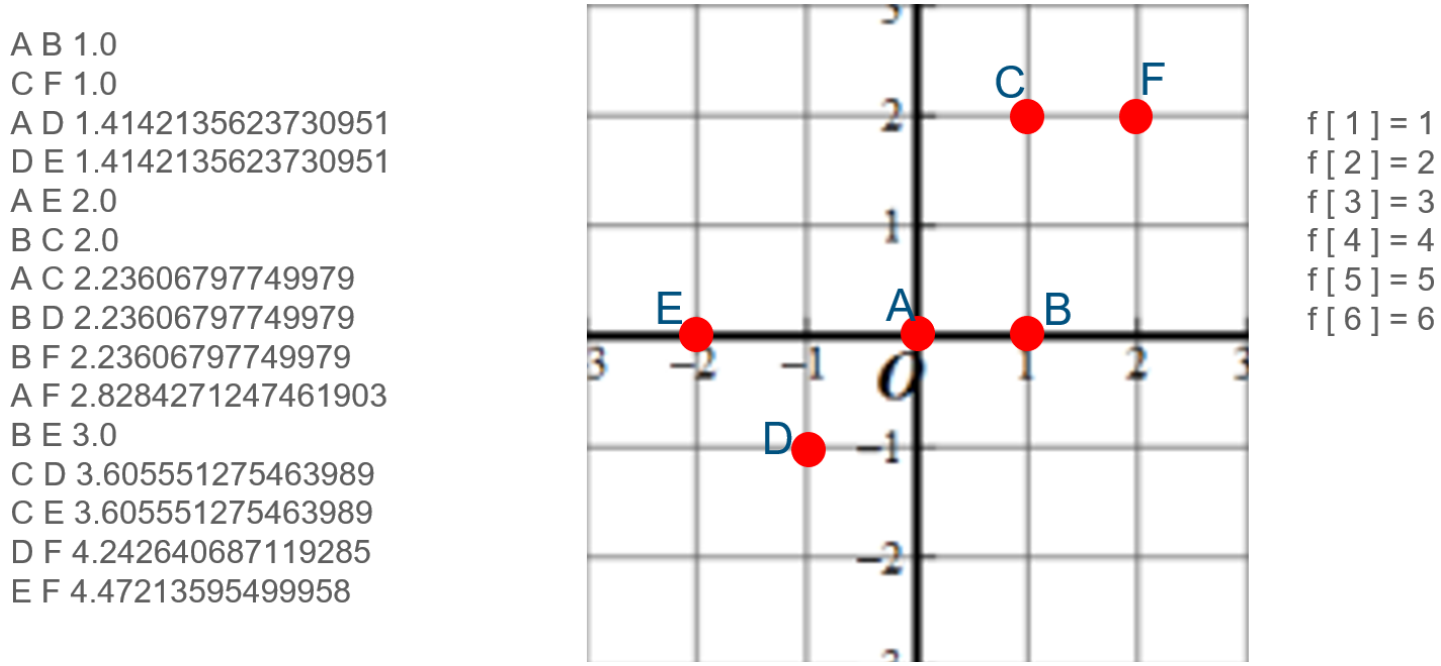
2.接下来,从最短距离开始,如果此路的起点和终点在一个整体中,便不对此边进行操作,否则,选择此条边,并更改 f f f 数组中的内容;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.util.ArrayList;
import java.util.Collections;
public class Main {
static int ans = 0;
static int n;
static int[] a;
static int m;
static int[] x;
static int[] y;
static double max;
static int[] f;
static int num = 0;
static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static void main(String[] args) throws IOException{
m = Integer.parseInt(in.readLine().trim());//猴子的数量
a = new int[m];//每一只猴子的最大跳跃距离
String[] s = in.readLine().trim().split(" ");
for(int i=0;i<m;i++)
a[i] = Integer.parseInt(s[i]);
n = Integer.parseInt(in.readLine().trim());//树的数量
x = new int[n];//每一棵树的横坐标
y = new int[n];//每一棵树的纵坐标
for(int i=0;i<n;i++) {
s = in.readLine().trim().split(" ");
x[i] = Integer.parseInt(s[0]);
y[i] = Integer.parseInt(s[1]);
}
ArrayList<Edge> list = new ArrayList<>();//存储Edge,获取顺序就是按照边长从小到大获取
for(int i=0;i<n-1;i++) {//起点
for(int j=i+1;j<n;j++) {//终点
double l = Math.sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));
Edge edge = new Edge(i, j, l);
list.add(edge);
}
}
Collections.sort(list);
f = new int[n];
for(int i=0;i<n;i++)
f[i] = i;
for(int i=0;i<list.size();i++) {
Edge e = list.get(i);
if(find(e.x)!=find(e.y)) {
merge(e.x,e.y);
max = Math.max(max, e.w);
num++;//用了多少条边
if(num==n-1)//最小生成树已经完成
break;
}
}
for(int i=0;i<m;i++)
if(a[i]>=max)
ans++;
System.out.println(ans);
}
static int find(int x) {//连接过的那一个点的最上一层
if(f[x] != x)
f[x] = find(f[x]);
return f[x];
}
static void merge(int x,int y) {//把两个点之间建立一个关系,表示这两个是一个整体
int xx = find(x);
int yy = find(y);
f[yy] = xx;
}
}
class Edge implements Comparable<Edge>{//起点、终点、边长
int x;
int y;
double w;
public Edge(int x, int y, double w) {
super();
this.x = x;
this.y = y;
this.w = w;
}
@Override
public int compareTo(Edge o) {//排序时是根据边的长度,从小到大排序
return this.w>o.w?1:-1;
}
}
最短路
D i s j k s t r a Disjkstra Disjkstra 算法(源点至其余点的最短距离)
思路:
1.用一个 d i s dis dis 数组存储结点,用一个数组 v i s i t visit visit 存储中转点;
2.每次从源点开始选择一个距离源点最近并且还未使用过的结点 u u u ,判断通过 u u u 能否中转到 v v v ,使 d i s t [ v ] dist[ v ] dist[v] 更小。即 d i s [ v ] dis[ v ] dis[v] = M a t h . m i n ( d i s [ v ] , d i s [ u ] + g [ u ] [ v ] ) Math.min(dis[ v ] , dis[ u ] + g[ u ][ v ] ) Math.min(dis[v],dis[u]+g[u][v]);
public static int[] Disjkstra(int vn,int[][] g){//结点数,两节点间距离
int[] dis = new int[vn];
int[] vis = new int[vn];
for(int i=0;i<vn;i++)
dis[i] = g[0][i];//初始化距离数组,0为源点
vis[0] = 1;//标记已经使用过了
int minindex = 0;//记录当前从v0到哪一个点距离最小
for(int i=0;i<vn-1;i++){
int min = Integer.MAX_VALUE;
for(int j=0;j<vn;j++){
if(vis[j]==0 && dis[j]<min){
min = dis[j];//记录最小的距离
minindex = j;//记录最小的结点编号
}
}
vis[minindex] = 1;
for(int j=0;j<vn;j++){
if(g[minindex][j]<Integer.MAX_VALUE && minindex!=j)
dis[j] = Math.min(dis[j],dis[minindex]+g[minindex][j]);
}
}
return dis;
}
优化:
1.已知 D i j k s t r a Dijkstra Dijkstra 算法每次在集合B中寻找能够加入集合 A A A 的顶点的时候,都要将符合条件的边进行遍历,当边较多的时候,该循环会带来较大的时间复杂度。
2.这里可以维护一个优先队列,队列中存放的是点(额外定义的一种数据类型),该点离顶点距离越小优先级越高。这样每次取队首元素,就可以得到当前状态下距离起点距离最短的点,并让其出队。若该点已在集合 A A A 中,则继续出队,否则将其加入集合 A A A ,并以该点为中介点进行松弛操作。(若此点 i i i 不在集合 A A A 中,则 d i s [ i ] dis[i] dis[i] 表示起点到点i的距离或起点到点 i i i 经过松弛之后的距离,若点i不在集合 A A A 中且其位于队首位置,那么它到集合 A A A 中某点的距离一定是最小的,这样便可保证我们取队首元素就能取到算法中描述的“最短边”如此一来便可以大大减小算法的时间复杂度。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
while (true) {
int n = cin.nextInt(), m = cin.nextInt();
if(n==0&m==0)break;
List<List<Edge>> vec = new ArrayList<>();
for (int i = 0; i < n + 5; i++) {
vec.add(new ArrayList<>());//点
}
int dis[] = new int[n + 5];
boolean vis[] = new boolean[n + 5];
for (int i = 0; i < m; i++) {
int a = cin.nextInt(), b = cin.nextInt(), c = cin.nextInt();//起点,终点,路长
vec.get(a).add(new Edge(b, c));
vec.get(b).add(new Edge(a,c));
}
for (int i = 0; i <= n; i++) {
dis[i] = Integer.MAX_VALUE;
vis[i] = false;
}
dis[1] = 0;
PriorityQueue<Node> queue = new PriorityQueue<>();
queue.add(new Node(1, 0));
while (!queue.isEmpty()) {
Node now = queue.poll();
if (vis[now.point]) {
continue;
}
vis[now.point] = true;
for (int i = 0; i < vec.get(now.point).size(); i++) {
Edge nxt = vec.get(now.point).get(i);
if (nxt.val + dis[now.point] < dis[nxt.to]) {
dis[nxt.to] = nxt.val + dis[now.point];
queue.add(new Node(nxt.to, dis[nxt.to]));
}
}
}
System.out.println(dis[n]);
}
}
}
class Edge{
int to,val;
public Edge(int to,int val){
this.to=to;
this.val=val;
}
}
class Node implements Comparable<Node>{
int point,val;
public Node(int point,int val){
this.val=val;
this.point=point;
}
@Override
public int compareTo(Node node){
return val-node.val;
}
}
F l o y d Floyd Floyd 算法(任意两点间的最短距离)
思路:以每一个点为中转结点,优化任意两点之间的距离;
public static void Floyd(){
for(int k=0;k<vn;k++){//中转点
for(int i=0;i<vn;i++){//起点
for(int j=0;j<vn;j++){//终点
if(i!=j && j!=k && i!=k && g[i][k]!=Integer.MAX_VALUE && g[k][j]!=Integer.MAX_VALUE)
g[i][j] = Math.min(g[i][j],g[i][k]+g[k][j]);
}
}
}
}























 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








