9.23模拟赛总结

最新推荐文章于 2024-07-23 17:36:37 发布

liang_2026

最新推荐文章于 2024-07-23 17:36:37 发布

阅读量39

点赞数

分类专栏：模拟赛总结文章标签：算法

本文链接：https://blog.csdn.net/weixin_55851276/article/details/133544922

版权

模拟赛总结专栏收录该内容

15 篇文章 0 订阅

订阅专栏

一.光之剑

题面：
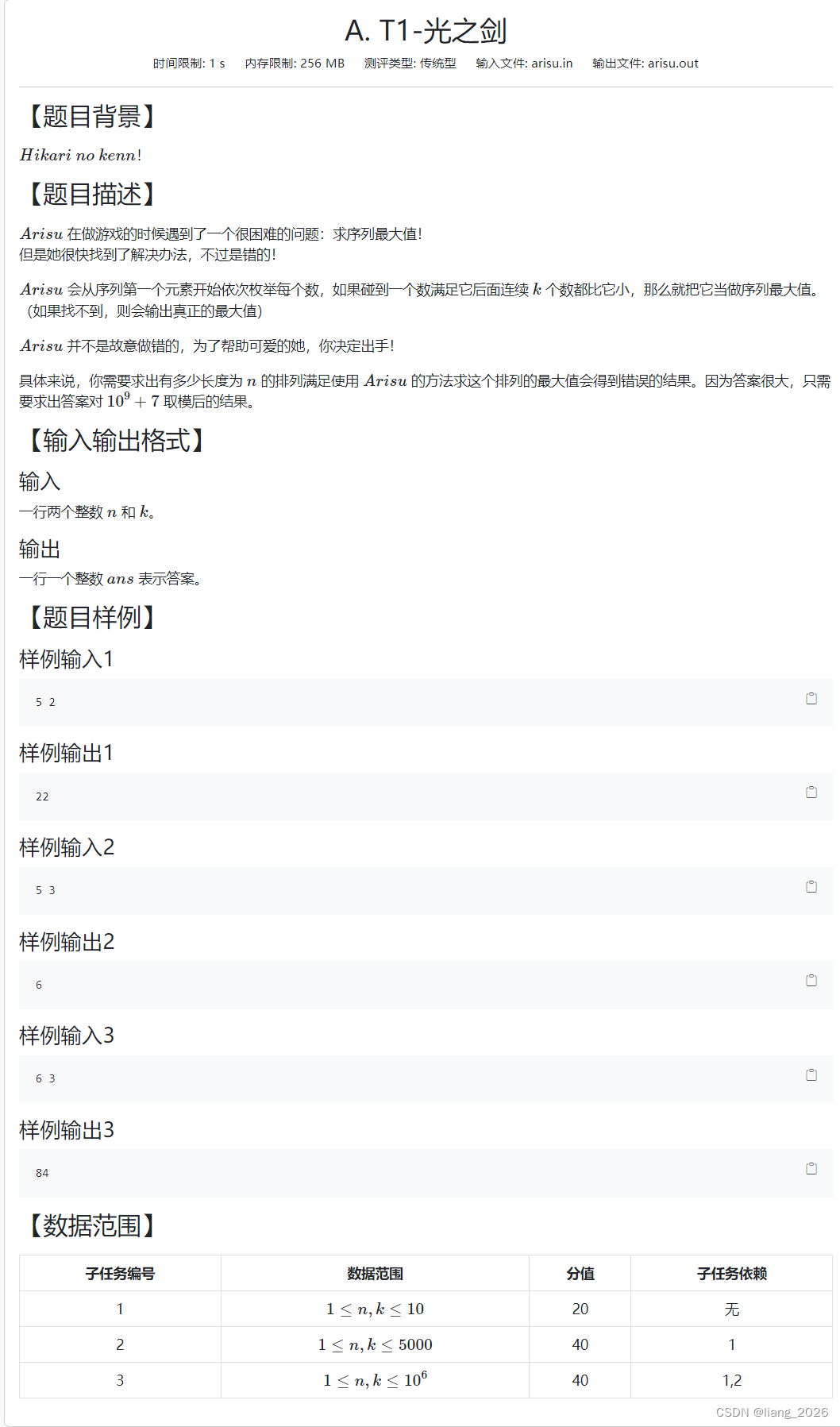
在这里插入图片描述

比较套路的DP，但很考察推式子的能力， ~~考场上A掉了~~ 。

分析：
题目中问的是有多少排列会得到错误的结果，但是得到错误的结果来源方式有很多，不太好搞。我们考虑 正难则反，计算出有多少排列会得到正确的结果，再用总排列数减去这个方案数就是答案。

考虑怎样求出 能得到正确结果的排列数。因为这是一个排列，所以最大值已经确定是 $n$ ，并且任何一个数都要比 $n$ 小。
想到得到正确结果的来源只有两种：

1.如果 $n$ 在某一个位置。如果这个位置后面还有至少 $k$ 个位置并且这个位置前面的数无法确定最大值，那么就可以找到正确的最大值。
2.整个排列都无法确定最大值，那么就可以找到正确的最大值。

我们发现第一种来源的第二个要求实际上是第二种来源方式的一个子问题，因为前面的数也一定各不相同，可以把它们离散化成一个更小的排列。而第一个要求可以通过枚举来满足。因此我们现在进一步转化问题：

求出有多少个 $[1, n]$ 的排列可以满足从前往后都找不到最大值。

设 $f_{i}$ 表示有多少个 $[1, i]$ 的排列满足从前往后都找不到最大值。考虑如何转移：因为 $i$ 是排列中最大的，所以需要满足两个条件：1. $i$ 所在的位置后面的位置数不到 $k$ 个。 2. $i$ 所在的位置前面放的数字也找不到最大值。因此，可以写出一下转移式：

$f_{i} = \sum_{j = i}^{i-k + 1}f_{j-1}* C_{i-1}^{j-1}*A_{i-j}^{i-j}$

这样转移复杂度是 $O(n^2)$ 的，我们将式子展开：

$f_{i} = \sum_{j = i-k+1}^{i}f_{j-1}* \frac{(i-1)!}{(j-1)!}$

发现此时转移的式子乘的系数的分母是不变的，当 $f_{i}$ 变成 $f_{i + 1}$ 时，会少一项的贡献，多一项的贡献，并且其他项会多乘一个 $i$ ，我们 $O (1)$ 的增减这两项，再多乘一个 $i$ 就可以了。时间复杂度 $O (n)$ 。

CODE：

#include<bits/stdc++.h>// res = 总的 - 找到对的 - 找不到的 
using namespace std;
const int N = 1e6 + 10;
typedef long long LL;
LL f[N], inv[N], fac[N], mod = 1e9 + 7, res;// f[i] 表示i个数的排列找不到最大值的方案数 
int n, k;
LL Pow(LL x, LL y){
	LL res = 1, k = x;
	while(y){
		if(y & 1) res = (res * k) % mod;
		y >>= 1;
	    k = (k * k) % mod;
	}
	return res;
}
void get(){
	fac[0] = 1;
	for(int i = 1; i < N; i++) fac[i] = ((fac[i - 1] * (1LL * i)) % mod);
	inv[N - 1] = Pow(fac[N - 1], mod - 2) % mod;
	for(int i = N - 2; i >= 0; i--) inv[i] = ((inv[i + 1] * (1LL * (i + 1))) % mod);
}
LL count(int k, int x){
	return (((f[k] * fac[x - 1]) % mod) * inv[k]) % mod;
}
LL C(int n, int m){
	return (((fac[n] * inv[m]) % mod) * inv[n - m]) % mod;
}
void Get_f(){
	f[0] = 1;
	for(int i = 1; i <= n; i++){
		f[i] = f[i - 1];
		if(i > k) f[i] = ((f[i] - count(i - k - 1, i - 1)) % mod + mod) % mod;
		f[i] = (f[i] * (1LL * (i - 1))) % mod;
		f[i] = (f[i] + count(i - 1, i)) % mod;
	}
}
int main(){
	freopen("arisu.in", "r", stdin);
	freopen("arisu.out", "w", stdout);
	cin >> n >> k;
	get();
	Get_f();
	for(int i = 1; i <= n - k; i++){//可以找到，枚举第 n 个数字的位置 
	    res = (res + (((f[i - 1] * C(n - 1, i - 1)) % mod) * (fac[n - i])) % mod) % mod;
	}
	res = (res + f[n]) % mod;//找不到
	res = ((fac[n] - res) % mod + mod) % mod;
	cout << res << endl;
	return 0;
}

二. 迈构

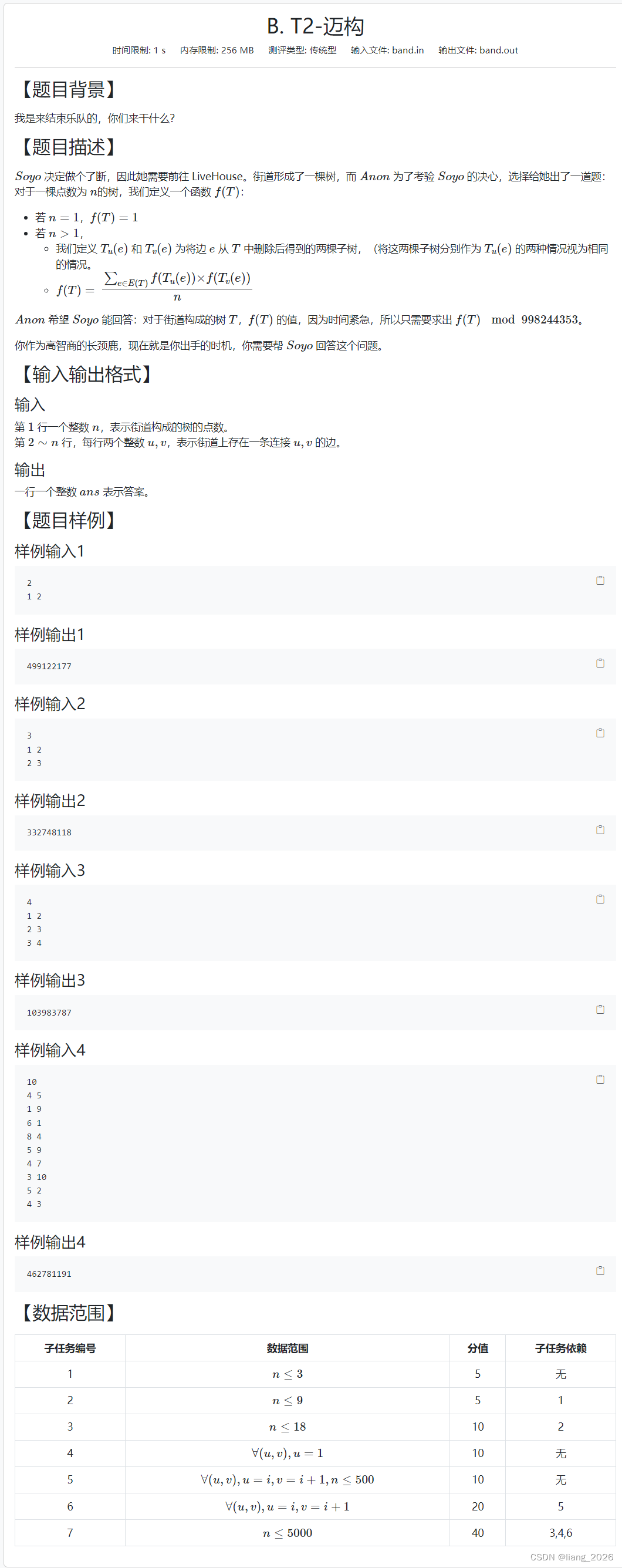
在这里插入图片描述

不会正解，分了好几段写。感觉挺考察分档的能力。

分析：

1. $\leq 18$ 时：我们注意到子树中的点一定也是原树中的点。因此可以状压。设 $dp_{mask}$ 表示点的状态为 $ma s k$ 所构成的树的答案。枚举其中存在的两个点，判断是否有边并断开即可。喜提 $20 pt s$ 。

2. 菊花图：我们发现断掉一条边后剩下一个更小的菊花和一个单点， $df s$ 搜出大小不同的菊花的答案即可。复杂度 $O (n)$ 。喜提 $10 pt s$ 。

3.链：发现长度相同的链最后的答案也一定相同，因此设 $f_{i}$ 表示长度为 $i$ 的链的答案，枚举端点做简单转移即可。又喜提 $30 pt s$ 。

4.正解：还不太会。

CODE：

#include<bits/stdc++.h>//60pts不知道可不可以搞 
using namespace std;
typedef long long LL;
const int N = 5100;
int n, u, v, dfn[N], rk, id[N], mask[N];
vector< int > E[N];
LL inv[N], mod = 998244353, f[1 << 18], num[1 << 18], dp[N];// dp[i] 表示前 i 个点的方案数 
bool mp[20][20];
LL Pow(LL x, LL y){
	LL res = 1, k = x;
	while(y){
		if(y & 1) res = (res * k) % mod;
		y >>= 1;
		k = (k * k) % mod;
	}
	return res % mod;
}
void dfs(int x, int fa){
	dfn[x] = rk; id[rk] = x;;//从0开始 
	mask[x] = (1 << rk);
	rk++;
	for(auto v : E[x]){
		mp[x][v] = 1;
		if(v == fa) continue;
		dfs(v, x);
		mask[x] |= mask[v];
	}
}
LL calc(int k){
	LL res = 0;
	for(int i = 0; i < n; i++){
		for(int j = i + 1; j < n; j++){
			if(((k >> i) & 1) && ((k >> j) & 1)){//考虑枚举两个点看有没有连边 
				if(mp[id[i]][id[j]]){// i 一定是 j 的父亲  
					res = (res + ((f[k & mask[id[j]]] * f[k ^ (k & mask[id[j]])]) % mod)) % mod;
				}
			}
		}
	}
	return (res * inv[num[k]]) % mod;
}
void solve1(){//状压 
	dfs(1, 0);//求dfs序 
	for(int i = 0; i < n; i++) f[1 << i] = 1;//初始化
	for(int i = 0; i < (1 << n); i++){
		if(!f[i]) f[i] = calc(i);
	} 
	printf("%lld\n", f[(1 << n) - 1] % mod);
}
LL count(int x){// x个节点的菊花图 
	if(x == 1) return 1LL;
    return ((((1LL * (x - 1)) * count(x - 1)) % mod) * inv[x]) % mod;
}
void solve2(){//菊花 
	LL res = 0;
	res = count(n) % mod;
	printf("%lld\n", res % mod);
}
void solve3(){//链 
	dp[1] = 1LL;
	for(int i = 2; i <= n; i++){
		for(int j = 1; j < i; j++){
			dp[i] = (dp[i] + ((dp[j] * dp[i - j]) % mod)) % mod;
		}
		dp[i] = (dp[i] * inv[i]) % mod;
	}
	printf("%lld\n", dp[n] % mod);
}
void solve4(){//不知道是啥 
	printf("%lld\n", (1LL * rand() * rand()) % mod);
}
LL getnum(int x){
	LL res = 0;
	while(x){res++; x -= (x & -x);}
	return res;
}
int main(){
	freopen("band.in", "r", stdin);
	freopen("band.out", "w", stdout);
	srand(time(0));
	bool flag1 = 1, flag2 = 1;
	scanf("%d", &n);
	for(int i = 0; i <= n; i++) inv[i] = Pow(1LL * i, mod - 2) % mod;
	for(int i = 0; i < (1 << 18); i++) num[i] = getnum(i);
	for(int i = 1; i < n; i++){
		scanf("%d%d", &u, &v);
		E[u].push_back(v);
		E[v].push_back(u);
		if(u != 1) flag1 = 0;
		if(v != u + 1) flag2 = 0;
	}
	if(n <= 18) solve1();//状压   20pts
	else if(flag1) solve2();//菊花 10pts
	else if(flag2) solve3();//链 30pts
	else solve4();//还不太会 
	return 0;
}
/*
3
1 2
2 3
*/

虽然这道题我不会，但是通过分段获得了 $60 pt s$ 的好成绩。所以以后不会的题要多写分段，多思考部分分。

三.醒幸

在这里插入图片描述

神奇的一道性质题，感觉挺显然，但就是没有想到。以后还要加强 推性质 的能力。

分析：

将删边转化成加边。我们对边按照边权从大到小排序，那么每次从剩下的边中选出 所连得两个节点不在同一集合 的边，并标记答案即可。复杂度 $O (K M)$ ，无法通过。

正解：我们可以构造出 $K$ 个点集，每个点集中的任意两个点都是不连通的。那么对于一条边而言，它能够第 $i$ 次被选中需要满足第 $i$ 个点集中这条边所连的两个点不连通。我们对于每一条边都找到最小的 $i$ 并在这个点集中将这两个点连上一条边即可。 关键性质：任意两个点的连通性从前往后都是单调的，即这两个点会在一些前缀点集中联通，在后面的点集中不连通。基于这个性质，我们就可以二分了。复杂度 $O(Mlog_2K)$ 。

CODE：

#include<bits/stdc++.h>//易得知任意两点连通性都是一个前缀 
using namespace std;
const int M = 3e5 + 10;
const int K = 1e4 + 10;
const int N = 1010;
int n, m, k, bin[K][N];
int cut[M];
struct edge{
	int u, v, w, id;
}E[M];
bool cmp(edge a, edge b){return a.w > b.w;}
int Find(int k, int x){return bin[k][x] == x ? x : bin[k][x] = Find(k, bin[k][x]);}
int query(int u, int v){
	int l = 1, r = k, mid, res = -1;
	while(l <= r){
		mid = (l + r >> 1);
		if(Find(mid, u) != Find(mid, v)) res = mid, r = mid - 1;
		else l = mid + 1;
	}
	return res;
}
int main(){
	freopen("hoshi.in", "r", stdin);
	freopen("hoshi.out", "w", stdout);
	scanf("%d%d%d", &n, &m, &k);
	for(int i = 1; i <= m; i++){
		scanf("%d%d%d", &E[i].u, &E[i].v, &E[i].w);
		E[i].id = i;
	}
	for(int i = 1; i <= k; i++){
		for(int j = 1; j <= n; j++){
			bin[i][j] = j;
		}
	}
	sort(E + 1, E + m + 1, cmp);
	for(int i = 1; i <= m; i++){
		int u = E[i].u, v = E[i].v, id = E[i].id;
		int now = query(u, v);
		if(now != -1){	
			int f1 = Find(now, u), f2 = Find(now, v);
			bin[now][f1] = f2;
			cut[id] = now;
		}
	}
	for(int i = 1; i <= m; i++) printf("%d\n", cut[i]);
	return 0;
}

四.亚梓莎

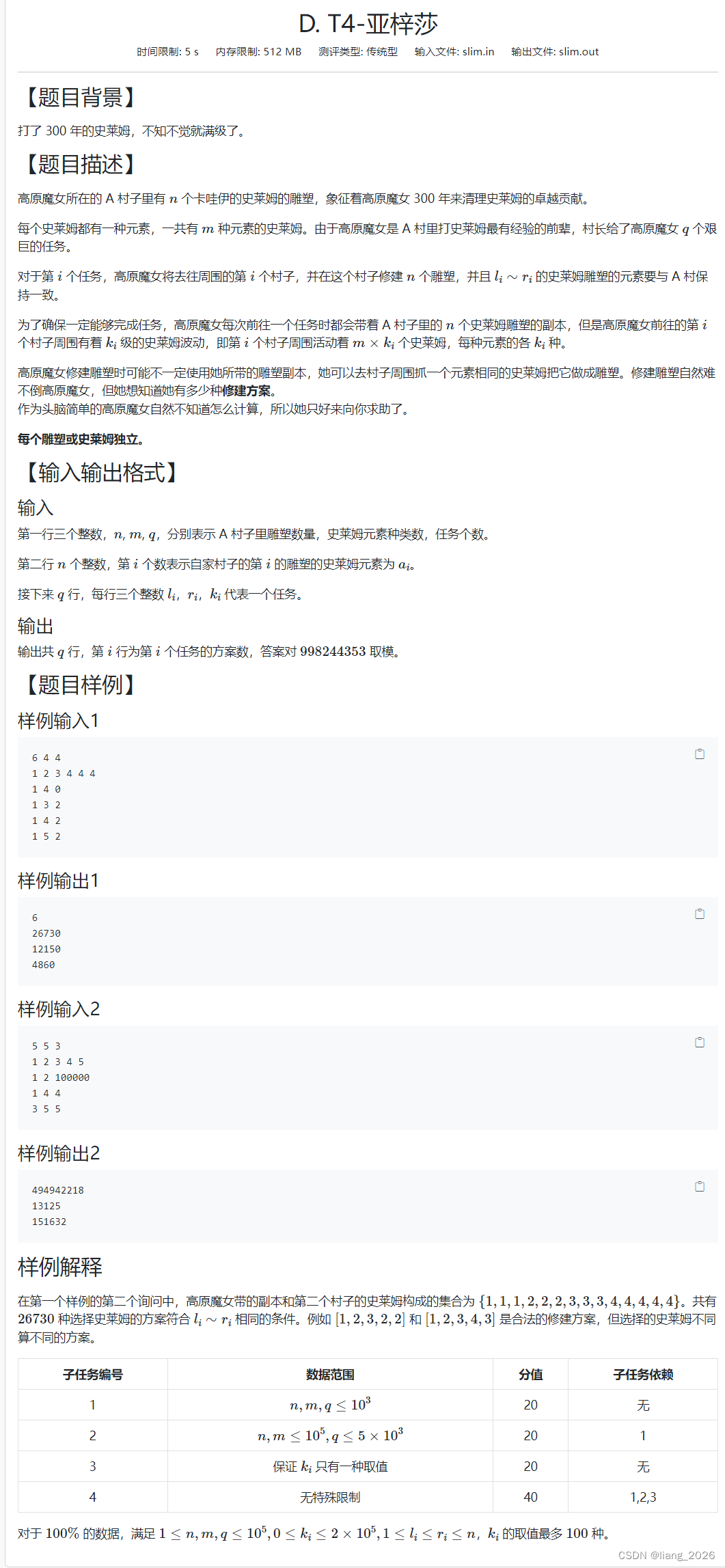
在这里插入图片描述

一道 莫队好题 ，考场上根本想不到，脑洞很大。看来以后还要增强对莫队的感知能力。

分析：

暴力不多说了，一些简单的排列组合式子即可拿到 $20 pt s$ 。
设一次询问中 $[l, r]$ 里每种雕塑的数量分别为 $c_i$ ， $[1, n]$ 中每种雕塑的数量分别为 $s_i$ 。那么答案就是 ${\textstyle \prod_{i=1}^{m} A_{si + k}^{c_i}} * A_{m*k+n-len}^{n-len}$ 。发现 $k$ 的取值很少，我们考虑根据 $k$ 对询问分类，然后在每一个 $k$ 里跑一遍莫队。跑莫队的过程中，延伸或缩短一个单位都可以 $O (1)$ 求出答案。块长需要特殊计算，卡卡时能够跑过。 ~~但是为什么我在Luogu上跑过了，校内OJ却跑不过！！！！！！~~ 。
还有一个坑点： $s q r t$ 返回的是 $d o u b l e$ ！！！！！！！！！！！！，因为这玩意儿调了一年。

CODE：

#include<bits/stdc++.h>//莫队大法好 
#define pb push_back
using namespace std;//考虑将所有k值一样的分成1类，每一类跑一遍莫队，离线计算答案即可
typedef long long LL;
const int N = 1e5 + 10;
const int K = 210;
int n, m, q, num[N], cnt, L[N], R[N], kk[N], a[N], bel[N], blo, s[N], Inv[N * 3];
LL ans[N], mod = 998244353;
inline int read(){
	int x = 0, f = 1; char c = getchar();
	while(!isdigit(c)){if(c == '-') f = -1; c = getchar();}
	while(isdigit(c)){x = (x << 1) + (x << 3) + (c ^ 48); c = getchar();}
	return x * f;
}
void write(LL x){
	if(x < 0) putchar('-'), x = -x;
	if(x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
inline LL Pow(LL x, LL y){
	LL res = 1, k = (x % mod);
	while(y){
		if(y & 1) res = (res * k) % mod;
		y >>= 1;
		k = (k * k) % mod;
	}
	return res;
}
struct range{int l, r, id;};
inline bool cmp(range a, range b){
    if(bel[a.l] != bel[b.l]) return bel[a.l] < bel[b.l];
    else{
    	if(bel[a.l] & 1) return a.r < b.r;
    	else return a.r > b.r;
	}
}
struct Mo_Team{//结构体里面跑，节省代码量
	vector< range > Q;
	int k, c[N]; LL res = 1, pre[N];// pre[i] 表示 (mk + 1) * (mk + 2) * ... * (mk + i) 在模 mod 下的数  
	inline void Get(){
		int qnum = Q.size();
		if((sqrt(qnum) == 0) || ((int)(n / sqrt(qnum)) == 0)) blo = sqrt(n);
		else blo = (n / sqrt(qnum));
		for(int i = 1; i <= n; i++) bel[i] = (i - 1) / blo + 1; 
		pre[0] = 1LL;
		for(int i = 1; i <= n; i++) pre[i] = (pre[i - 1] * ((1LL * m * k + 1LL * i) % mod)) % mod;//等会儿用 
	}
	inline void add(int l, int r, int p){
		res = (res * (1LL * k + s[a[p ? r : l]] - c[a[p ? r : l]])) % mod;
		c[a[p ? r : l]]++;
	}
	inline void del(int l, int r, int p){
		res = (res * Inv[k + s[a[p ? r : l]] - c[a[p ? r : l]] + 1]) % mod;
		c[a[p ? r : l]]--;
	}
	inline void solve(){
	    Get();
		sort(Q.begin(), Q.end(), cmp);
		int L = 1, R = 0;
		for(auto x : Q){
			while(L > x.l) add(--L, R, 0);
			while(R < x.r) add(L, ++R, 1);
			while(L < x.l) del(L++, R, 0);
			while(R > x.r) del(L, R--, 1);
			ans[x.id] = (res * pre[n - (R - L + 1)]) % mod;
		}
	}
}mo[K]; 
int main(){
	n = read(), m = read(), q = read();
	for(register int i = 0; i < N * 3; i++) Inv[i] = Pow(1LL * i, mod - 2) % mod;//预处理逆元 
	for(register int i = 1; i <= n; i++) s[a[i] = read()]++;
	for(register int i = 1; i <= q; i++){
		L[i] = read(), R[i] = read(), kk[i] = read();
		num[++cnt] = kk[i];
	}
	sort(num + 1, num + cnt + 1);
	cnt = unique(num + 1, num + cnt + 1) - (num + 1);
	for(register int i = 1; i <= q; i++){
		int c = lower_bound(num + 1, num + cnt + 1, kk[i]) - num;
		mo[c].Q.pb((range){L[i], R[i], i});
		mo[c].k = kk[i];
	}
	for(int i = 1; i <= cnt; i++) mo[i].solve();
	for(int i = 1; i <= q; i++) write(ans[i] % mod), putchar('\n');
	return 0;
}

总结：还要提升自己推性质的能力，脑洞还要大一点。

liang_2026

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
9.23模拟赛总结

分析：题目中问的是有多少排列会得到错误的结果，但是得到错误的结果，不太好搞。我们考虑，计算出有多少排列会得到正确的结果，再用总排列数减去这个方案数就是答案。考虑怎样求出。因为这是一个排列，所以最大值已经确定是n，并且任何一个数都要比n小。想到得到正确结果的来源只有两种：1.如果n在某一个位置。如果这个位置后面还有至少k个位置并且，那么就可以找到正确的最大值。2.整个排列都无法确定最大值，那么就可以找到正确的最大值。我们发现第一种来源的第二个要求实际上是第二种来源方式的一个。
复制链接

扫一扫

专栏目录