C语言实现牛顿迭代法（Newton-Raphson Method）

目录

前言

A.建议

B.简介

一 代码实现

二 时空复杂度

A.时间复杂度

B.空间复杂度

C.总结

三 优缺点

A.优点：

B.缺点：

C.总结：

四 现实中的应用

---

前言

A.建议

1.学习算法最重要的是理解算法的每一步，而不是记住算法。

2.建议读者学习算法的时候，自己手动一步一步地运行算法。

B.简介

牛顿迭代法（Newton-Raphson Method）是一种高效的数值方法，用于求解实数域或复数域上非线性方程 f(x)=0 的根。该方法基于函数 f在某一点处的泰勒级数展开，并利用一阶导数 f′(x)近似地构造一条切线，通过切线与 xx-轴的交点来更新估计的根。迭代过程持续进行，直至达到预定的精度要求。

一 代码实现

以下是使用C语言实现牛顿迭代法的基本步骤和代码示例：

步骤一：定义目标函数 f(x) 和其导数 f′(x)

首先，你需要编写两个函数：一个表示目标非线性方程 f(x)，另一个表示其导数 f′(x)。这两个函数应接受浮点数作为输入参数，并返回相应的浮点数结果。

// 目标函数 f(x)
float function_f(float x) {
    // 实现具体的非线性函数，例如：x^3 - ½ x - ⅓
    return pow(x, 3) - 0.5 * x - 1.0 / 3.0;
}

// 导数 f'(x)
float derivative_f(float x) {
    // 实现函数 f(x) 的一阶导数，例如：3x^2 - 0.5
    return 3 * pow(x, 2) - 0.5;
}

步骤二：实现牛顿迭代算法

接下来，编写一个主函数，其中包含牛顿迭代的核心逻辑。该函数通常接收以下参数：

• 初始猜测值 x_initial
• 目标精度 tolerance
• 最大迭代次数 max_iterations（防止陷入无限循环）

在每次迭代中，按照牛顿迭代公式更新估计根：

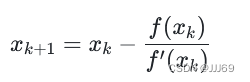
同时检查是否达到终止条件（即误差小于给定的精度或达到最大迭代次数）。

#include <stdio.h>
#include <math.h>

#define MAX_ITERATIONS 1000
#define TOLERANCE 1e-6

// ... 上面定义的 function_f 和 derivative_f 函数 ...

void newton_raphson(float x_initial, float tolerance, int max_iterations) {
    float x_current = x_initial;
    float x_next;
    float error;

    int iteration_count = 0;

    while (iteration_count < max_iterations) {
        x_next = x_current - function_f(x_current) / derivative_f(x_current);
        error = fabs(x_next - x_current);

        if (error <= tolerance) {
            printf("Root found after %d iterations: %.6f\n", iteration_count + 1, x_next);
            break;
        }

        x_current = x_next;
        iteration_count++;
    }

    if (i