前言
最近在学习高频电子线路中的串联谐振回路和并联谐振回路相关知识,特以此文进行总结、归纳,以便日后进行查询和复习。
| 串联谐振(电压谐振) | 并联谐振(电流谐振) | ||
| 定义 | 由信号源与电容、电感串联构成的振荡回路 | 由信号源与电容、电感线圈并联的振荡回路 | |
| 电路图 | 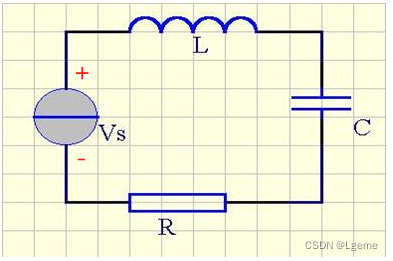 |  | |
| 阻抗 | 阻抗、 导纳、 谐振电阻 | | |
| 回路电抗 | 回路电纳 | ||
| 回路电流 | 并联回路两端电压 | ||
| 谐振频率 | | 谐振频率 | |
| 回路电流达到最大值 | 并联两端电压达到最大值 | ||
| 电抗与频率关系 | 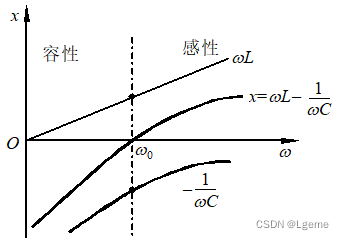 | 电纳与频率关系 | 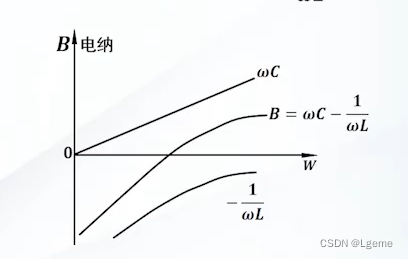 |
| 特性阻抗 | 特性阻抗 | ||
| 品质因数 | 品质因数 | | |
| 电感、电容两端电压 | | 电容、电感的支路电流 | |
| 谐振曲线表达式 | | 并联谐振曲线表达式 | |
| 广义失谐系数 | 广义失谐系数 | | |
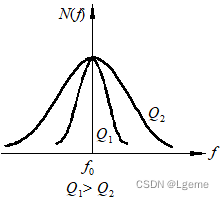
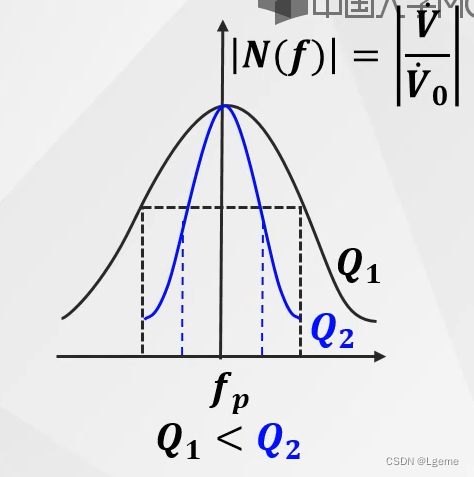
| 串联振荡电路谐振曲线 |
Q值大曲线尖锐,选择性好,Q值小曲线钝,通带宽 | 并联振荡电路谐振曲线 |
Q值大曲线尖锐,选择性好,Q值小曲线钝,通带宽 |
| 通频带 | 通频带 | ||
| 考虑电源内阻和负载 |
结论: 1:Rs+RL使回路Q值降低,从而使谐振曲线变钝 2:串联谐振回路通常适用于信号源内阻Rs很小(恒压源)和负载电阻RL也不大的情况 | 考虑电源内阻和负载 |
结论: 并联谐振适合电源内阻和负载很大的电路 |
总结:
以上就是对串联谐振电路和并联谐振电路性质的总结,谢谢你能观看到这。


























 1790
1790

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










